Let $a_{1} & a_{2}$ are the acceleration of A & B. Let $b_{1} & b_{2}$ the acceleration of C & D relative to the wedges A and B respectively, choose the right relation. (directions of $a_{1}, a_{2}, b_{1} & b_{2}$ are shown in figure below) :

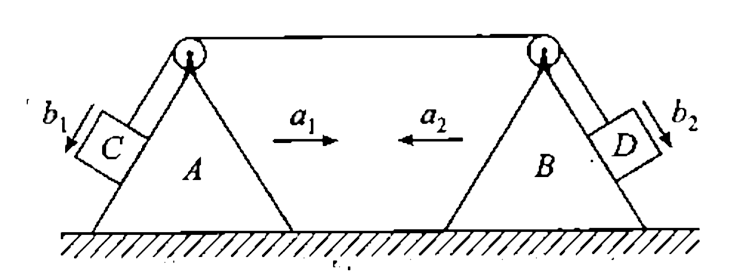
$a_{1} - a_{2} + b_{1} - b_{2} = 0$

$a_{1} + a_{2} - b_{1} - b_{2} = 0$

$a_{1} + a_{2} + b_{1} + b_{2} = 0$

$a_{1} + b_{2} = a_{2} + b_{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for Let a_(1) & a_(2) are the acceleration of A & B. Let b_(1) & b_(2) the acceleration of C & D relative to the wedges A and B respectively, choose the right relation. (directions of a_(1), a_(2), b_(1) & b_(2) are shown in figure below) : by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Let ${\to a}_{1}$ and ${\to a}_{2}$ are the acceleration of wedges A and B. Let ${\to b}_{1}$ and ${\to b}_{1}$ be the accelerations of C and D relative to wedges A and B respectively. Choose the right relation $:$

A ${\to a}_{1} - {\to a}_{2} + {\to b}_{1} - {\to b}_{2} = 0$
B ${\to a}_{1} + {\to a}_{2} + {\to b}_{1} + {\to b}_{2} = 0$
C ${\to a}_{1} + {\to a}_{2} - {\to b}_{1} - {\to b}_{2} = 0$
D ${\to a}_{1} + 2 {\to b}_{2} = 2 {\to a}_{2} - {\to b}_{1} = 0$
Question 2 - Select One
If the equation of the locus of a point equidistant from the points $(a_{1}, b_{1}$ , and $(a_{2}, b_{2})$ is
$(a_{1} - a_{2}) x + (b_{1} - b_{2}) y + c = 0$ , then the value of c is
A $\frac{1}{2} (a_{2}^{2} + b_{2}^{2}) - (a_{1}^{2} - b_{1}^{2})$
B $(a_{1}^{2} - a_{2}^{2} + b_{1}^{2} - b_{2}^{2})$
C $\frac{1}{2} (a_{1}^{2} + a_{2}^{2} + b_{1}^{2} + b_{2}^{2})$
D $\sqrt{(a_{1}^{2} + b_{1}^{2} - a_{2}^{2} - b_{2}^{2})}$
Question 3 - Select One
Let $a_{1}, a_{2}, \dots .$ and $b_{1}, b_{2}, \dots .$ be arithemetic progression such that $a_{1} = 25$ , $b_{1} = 75$ and $a_{100} + b_{100} = 100$ , then the sum of first hundred term of the progression $a_{1} + b_{1}$ , $a_{2} + b_{2}$ ,…. is equal to
A $1000$
B $100000$
C $10000$
D $24000$

PHYSICS GALAXY - ASHISH ARORA-NEWTONS LAWS OF MOTION-Conceptual MCQs

Home
Ask Doubt
Profile

Let a1&a2 are the acceleration of A & B. Let b1&b2 the acceleration of C & D relative to the wedges A and B respectively, choose the right relation. (directions of a1,a2,b1&b2 are shown in figure below) :

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let →a1 and →a2 are the acceleration of wedges A and B. Let →b1 and →b1 be the accelerations of C and D relative to wedges A and B respectively. Choose the right relation :

If the equation of the locus of a point equidistant from the points (a1,b1, and (a2,b2) is (a1−a2)x+(b1−b2)y+c=0, then the value of c is

Let a1,a2,…. and b1,b2,…. be arithemetic progression such that a1=25, b1=75 and a100+b100=100, then the sum of first hundred term of the progressiona1+b1, a2+b2,…. is equal to

PHYSICS GALAXY - ASHISH ARORA-NEWTONS LAWS OF MOTION-Conceptual MCQs

Let $a_{1} & a_{2}$ are the acceleration of A & B. Let $b_{1} & b_{2}$ the acceleration of C & D relative to the wedges A and B respectively, choose the right relation. (directions of $a_{1}, a_{2}, b_{1} & b_{2}$ are shown in figure below) :

Let ${\to a}_{1}$ and ${\to a}_{2}$ are the acceleration of wedges A and B. Let ${\to b}_{1}$ and ${\to b}_{1}$ be the accelerations of C and D relative to wedges A and B respectively. Choose the right relation $:$

If the equation of the locus of a point equidistant from the points $(a_{1}, b_{1}$ , and $(a_{2}, b_{2})$ is
$(a_{1} - a_{2}) x + (b_{1} - b_{2}) y + c = 0$ , then the value of c is

Let $a_{1}, a_{2}, \dots .$ and $b_{1}, b_{2}, \dots .$ be arithemetic progression such that $a_{1} = 25$ , $b_{1} = 75$ and $a_{100} + b_{100} = 100$ , then the sum of first hundred term of the progression $a_{1} + b_{1}$ , $a_{2} + b_{2}$ ,…. is equal to