Let Q and W denote the amount of heat given to an ideal gas the work done by it in an isothermal process.
Q=0
W=0
Q≠W
Q=W
The correct Answer is:D
To solve the problem, we need to analyze the relationship between heat (Q), work done (W), and internal energy change (ΔU) for an ideal gas undergoing an isothermal process.
1. Understanding the Isothermal Process:
- In an isothermal process, the temperature of the system remains constant. Therefore, the change in temperature (ΔT) is zero.
- Since temperature is constant, the internal energy of an ideal gas, which depends only on temperature, also remains constant.
2. Change in Internal Energy:
- The change in internal energy (ΔU) for an ideal gas can be expressed as:
ΔU=f2nRΔT
where f is the degrees of freedom, n is the number of moles, and R is the universal gas constant.
- Since ΔT = 0 for an isothermal process, we have:
ΔU=0
3. Applying the First Law of Thermodynamics:
- The First Law of Thermodynamics states:
Q=ΔU+W
- Substituting ΔU = 0 into the equation gives:
Q=0+W
or simply,
Q=W
4. Conclusion:
- From the above analysis, we conclude that for an ideal gas undergoing an isothermal process, the heat added to the gas (Q) is equal to the work done by the gas (W).
- Therefore, the correct answer is:
Q=W
Final Answer:
The correct option is D: Q=W.
- In an isothermal process, the temperature of the system remains constant. Therefore, the change in temperature (ΔT) is zero.
- Since temperature is constant, the internal energy of an ideal gas, which depends only on temperature, also remains constant.
- The change in internal energy (ΔU) for an ideal gas can be expressed as:
ΔU=f2nRΔT
where f is the degrees of freedom, n is the number of moles, and R is the universal gas constant.
- Since ΔT = 0 for an isothermal process, we have:
ΔU=0
- The First Law of Thermodynamics states:
Q=ΔU+W
- Substituting ΔU = 0 into the equation gives:
Q=0+W
or simply,
Q=W
- From the above analysis, we conclude that for an ideal gas undergoing an isothermal process, the heat added to the gas (Q) is equal to the work done by the gas (W).
- Therefore, the correct answer is:
Q=W
The correct option is D: Q=W.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The specific heat of a gas in an isothermal process is
AinfiniteBzeroCnegativeDremains constantAssertion : In an isothemal expansion the gas absorbs heat and does work .
Reason: In an isothermal process there is no change in internal energy of an ideal gas.ABoth assertion and reason are true and reason is the correct explanation of assertionBBoth assertion and reason are true but reason is not the correct explanation of assertionCAssertion is true but reason is falseDBoth assertion and reason are false.
If heat is supplied to an ideal gas in an isothermal process.
View SolutionCan a process on an ideal gas be both adiabatic and isothermal. ?
View SolutionThe figures given below show different processes (relating pressure P and volume V) for a given amount of an ideal gas. W is work done by the gas and ΔQ is heat absorbed by the gas.
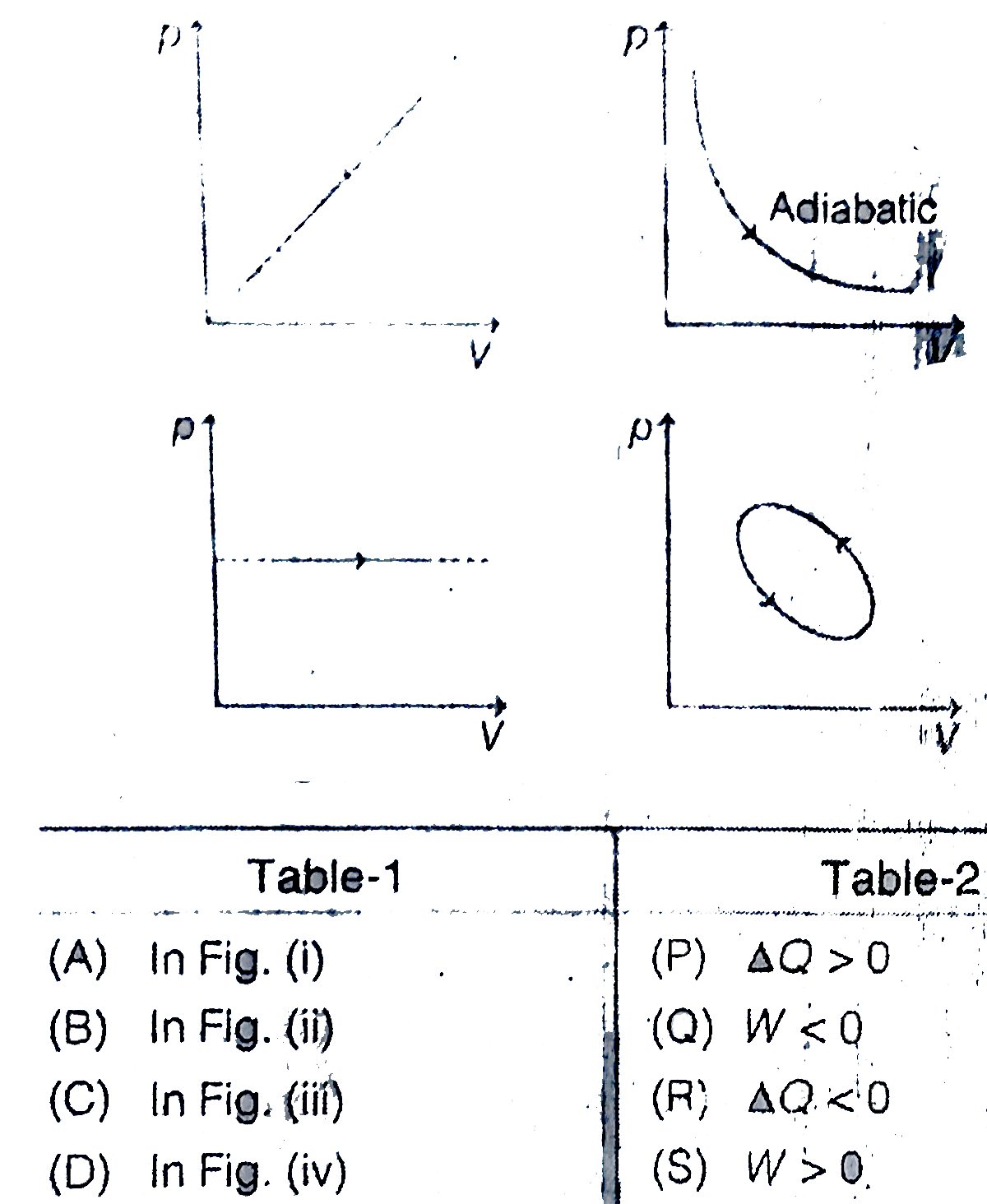
View SolutionIn an isothermal process for an ideal gas
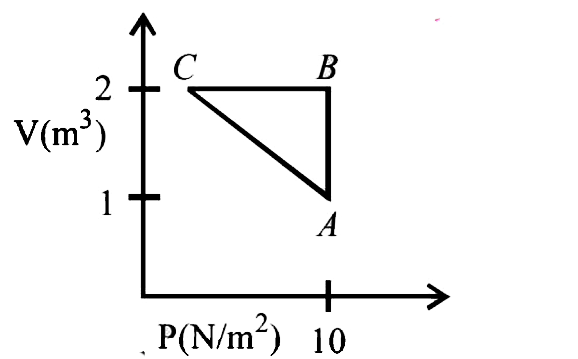
View SolutionAn ideal gas is taken through the cycle A→B→C→A, as shown in the figure, If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process CtoA is
View SolutionIf Q, E and W denote respectively the heat added, change in internal energy and the work done in a closed cycle process, then
View Solution
