Let TaandTb be the final temperatures of the samples A and B respectively in the previous question.
Ta<Tb
Ta=Tb
Ta>Tb
The relation between TaandTb cannot be deduced.
The correct Answer is:A
Step by step video, text & image solution for Let T_a and T_b be the final temperatures of the samples A and B respectively in the previous question. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Objective 2
7 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Exercises
35 Videos
- SPECIFIC HEAT CAPACITIES OF GASESBOOK - HC VERMACHAPTER - SPECIFIC HEAT CAPACITIES OF GASESEXERCISE - Short Answer
10 Videos
- SOUND WAVESBOOK - HC VERMACHAPTER - SOUND WAVESEXERCISE - Exercises
89 Videos
- THE FORCESBOOK - HC VERMACHAPTER - THE FORCESEXERCISE - Exercises
12 Videos
Similar Questions
Figure shows variation of intensity per unit wavelength (Radiance) with wavelength for radiation coming from two source A and B. Let TAandTB be temperature of source A and B respectively and dAanddB be distance of source from detector, then–
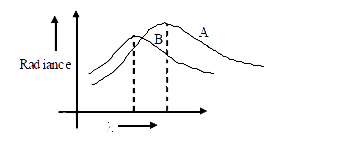
View SolutionA sphere A is placed at smooth table. An another sphere B is suspended as shown in figure. Both spheres are identical in all respects. Equal quantity of heat is supplied to both spheres. All kiinds of heat loss are neglected. The final temperatures of A and B are TA and TB respectively, then

View Solution
Knowledge Check
Let p1 and p2 be the final pressure of the samples and 2 respectively in the previous question then.
Ap1>p2Bp1=p2Cp1<p2DThe relation between p1 and p2 cannot be deducedLet (ΔWa)and(ΔWb) be the work done by the system A and B respectively in the previous question.
AΔWa>ΔWbBΔWa=ΔWbCΔWa<ΔWbDThe relation between ΔWaandΔWb cannot be deduced.The value of (Cp−Cv) is 1.00R for a gas sample in state A and is 1.08 R in state B. Let (pA,pB)denote the pressures and (TAandTB) denote the temperatures of the states A and B respectively . Most likely
ApA<pB and TA>TBBpA>pBandTA<TBCpA=pBandTA<TBDpA>pBandTA=TB
A ball is hanging vertically by a light inextensible string of length L from fixed point O. The ball of mass m is given a speed u at the lowest position such that it completes a vertical circle with centre at O as shown. Let AB be a diameter of circular path of ball making an angle θ with vertical as shown. (g is acceleration due to gravity)
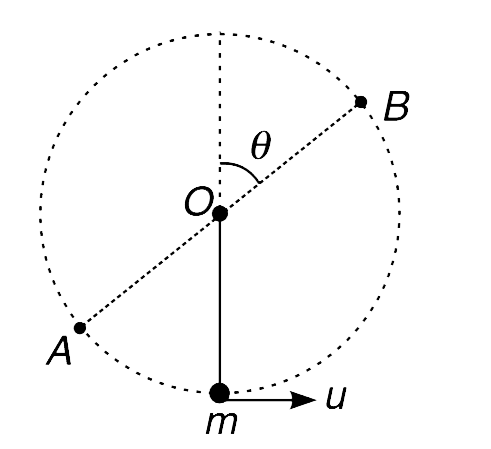
a) Let TA and TB be tension in string when ball is at A and B respectively, then find TA – TB. (b) Let →aA and →aB be acceleration of ball when it is at A and B respectively, then find the value of |→aA+→aB|
View SolutionIf AT and BT are transpose matrices of the square matrices A and B respectively, then(AB)T is equal to
View SolutionTwo different ideal diatomic gases A and B are initially in the same state. A and B are then expanded to same final volume through adiabatic and isothermal process respectively. If PA,PB and TA,TB represents the final pressure and temperature of A and B respectively then.
View SolutionIn an adiabatic expansion of a gas initial and final temperatures are T1and T2 respectively, then the change in internal energy of the gas is
View Solution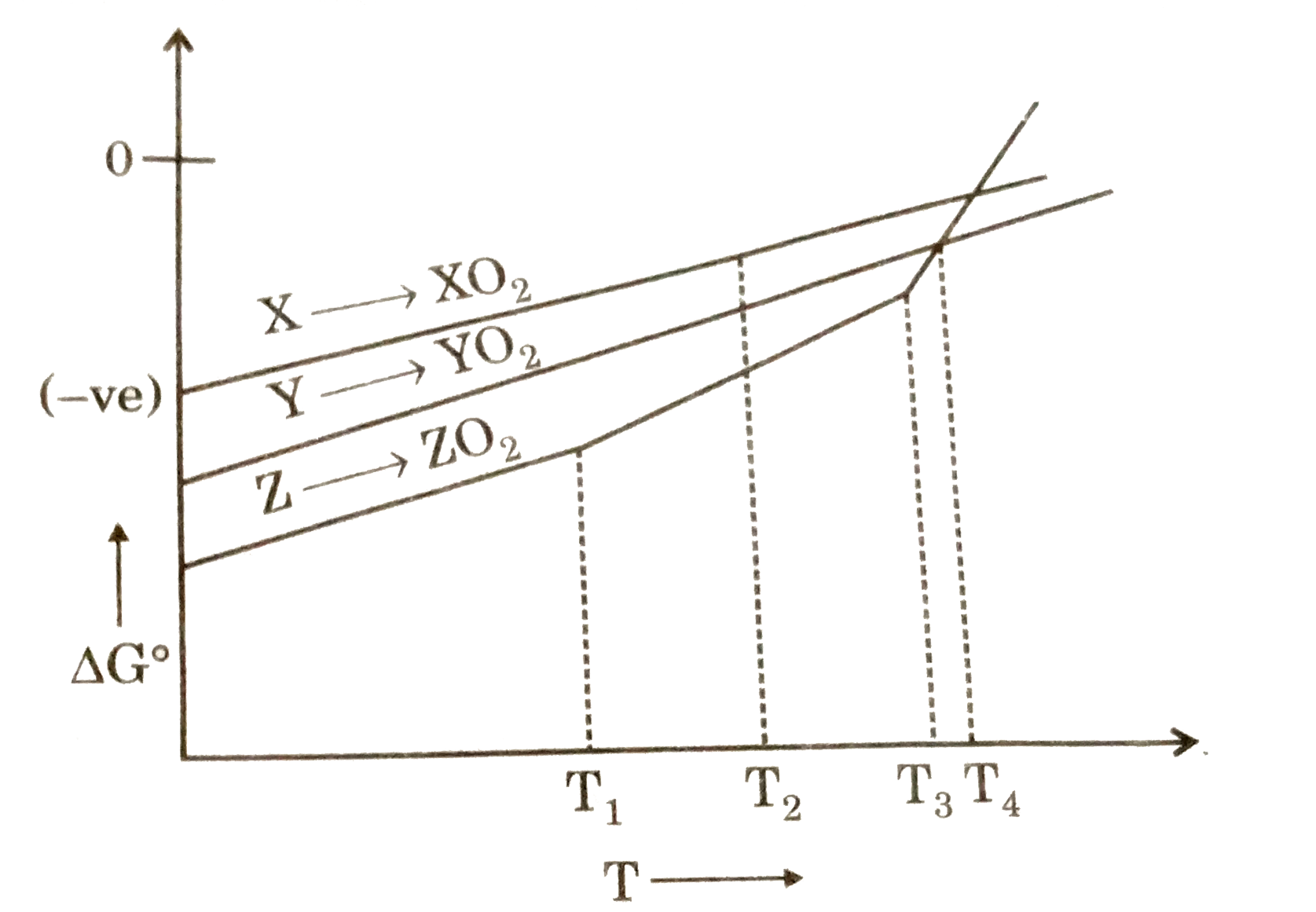
Temperature T1andT3 represents respectively:
View Solution
