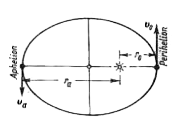
Let the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

The magnitude of the angular momentum at P is Lp=mPrpup. Since inspection tells us that rp and vp are mutually perpendicular. Similarly . LA=mprA.vA. From angular momentum conservation
mprpvp=mprAvA
or vpvA=rArp
The area, SBAX bounded by the elipse and the raidus vectors SB and SC is large than SBPC in Fig. 9.1 From kepler's second law, equal areas are swept in equal times. Hence the planat will take a longer time to traverse BAC than CPB.
Topper's Solved these Questions
Similar Questions
Let the speed of the planet at the perihelion P in figure be vP and the Sun planet distance SP be rP. Relater rP,vP to the corresponding quantities at the aphelion (rA,vA). Will the planet take equal times to transverse BAC and CPB?

View SolutionA speed of the palnet at the perihelion P be Vp and the sun -planet distance SP be rP as shown in fig. Relate {rp,vp} to the corresponding quantities at the aphelion {rA,VA}. Will the planet take equal times to traverse BAC and CPB?
View Solution
Knowledge Check
A: The speed of a planet is maximum at perihelion .
R : The angular momentum of a planet about centre of sun is conserved .AIf both Assertion & Reason are true . And the reason is the correct explanation of the assertion , then mark (1)BIf both Assertion & Reason are true but the reason is not the correct explanation of the assertion , then mark (2)CIf Assertion is true statement but Reason is false , then mark (3)DIt will move the same speed , tangentially to the spacecraftIf r denotes the mean distance of a planet from the sun and T is the time period of planet, then
Ar∝T2/3Br∝T3/2Cr∝T1/3Dr∝TThe period of revolution of a planet around the sun is 8 times that of the earth. If the mean distance of that planet from the sun is r, then mean distance of earth from the sun is
Ar/2B2rCr/4D4r
The point of an elliptical orbit closest to the Sun is called the perihelion, and the point most distant from it is called aphelion (Fig). Denoting the distance from the perihelion to the Sun by r0 and the velocity of the planet at the perihelion by v0 , find the radius of curvature of the orbit at the perihelion and at the aphelion, the distance from the aphelion to the Sun, and the velocity of the planet at the aphelion.
Prove that the motion of a planet in an elliptical orbit is only possible, if its total energy is negative.
View SolutionThe radius of a planet is twice that of the earth but its average density is the same. If the escape speed at the planet and at the earth are vp and ve, respectively, then prove that vp=2ve
View SolutionA planet moves around the sun. At a given point P, it is closest from the sun at a distance d1 and has a speed v1. At another point Q, when it is farther from the sun at a distance d2, its speed will be
View SolutionA planet moves around the sun. At a given point P, it is closest from the sun at a distance d1 and has a speed v1 At another point Q, when it is farthest from the sun at a distance d2 its speed will be
View SolutionA planet moves around the sun. at a given point P, it is closest from the sun at a distance d1, and has a speed V1. At another point Q, when it is farthest from the sun at a distance d2, its speed will be
View Solution
