Light from a hydrogen tube is incident on the cathode of a photoelectric cell the work function of the cathode surface is 4.2eV. In order to reduce the photo - current to zero the voltage of the anode relative to the cathode must be made
−4.2V
−9.4V
−17.8V
+9.4V
The correct Answer is:B
To solve the problem, we need to determine the stopping potential required to reduce the photocurrent to zero when light from a hydrogen tube is incident on the cathode of a photoelectric cell. The work function of the cathode surface is given as 4.2 eV.
1. Identify the Energy of the Incident Light:
The energy of the incident photon from the hydrogen tube can be calculated using the formula for the energy levels of hydrogen:
E=−13.6eVn2
For the ground state (n = 1), the energy is:
E=−13.6eV(this is the energy required to remove the electron)
However, when considering the energy of the photon that can eject an electron, we take the positive value:
Ephoton=13.6eV
2. Calculate the Maximum Kinetic Energy of Ejected Electrons:
The maximum kinetic energy (K.E.) of the photoelectrons can be calculated using the equation:
K.E.=Ephoton−ϕ
where ϕ is the work function of the cathode. Given ϕ=4.2eV:
K.E.=13.6eV−4.2eV=9.4eV
3. Determine the Stopping Potential:
To reduce the photocurrent to zero, we need to apply a stopping potential (V0) that will counteract the kinetic energy of the ejected electrons. The relationship between the loss in kinetic energy and the gain in potential energy is given by:
K.E.=e⋅V0
where e is the charge of the electron (which cancels out in the equation). Thus, we can set:
9.4eV=e⋅V0
Therefore, the stopping potential V0 required is:
V0=−9.4V
The negative sign indicates that the potential is applied in the opposite direction to the motion of the electrons.
4. Conclusion:
The voltage of the anode relative to the cathode must be made −9.4V to reduce the photocurrent to zero.
Final Answer:
The voltage of the anode relative to the cathode must be made -9.4 V.
---
The energy of the incident photon from the hydrogen tube can be calculated using the formula for the energy levels of hydrogen:
E=−13.6eVn2
For the ground state (n = 1), the energy is:
E=−13.6eV(this is the energy required to remove the electron)
However, when considering the energy of the photon that can eject an electron, we take the positive value:
Ephoton=13.6eV
The maximum kinetic energy (K.E.) of the photoelectrons can be calculated using the equation:
K.E.=Ephoton−ϕ
where ϕ is the work function of the cathode. Given ϕ=4.2eV:
K.E.=13.6eV−4.2eV=9.4eV
To reduce the photocurrent to zero, we need to apply a stopping potential (V0) that will counteract the kinetic energy of the ejected electrons. The relationship between the loss in kinetic energy and the gain in potential energy is given by:
K.E.=e⋅V0
where e is the charge of the electron (which cancels out in the equation). Thus, we can set:
9.4eV=e⋅V0
Therefore, the stopping potential V0 required is:
V0=−9.4V
The negative sign indicates that the potential is applied in the opposite direction to the motion of the electrons.
The voltage of the anode relative to the cathode must be made −9.4V to reduce the photocurrent to zero.
The voltage of the anode relative to the cathode must be made -9.4 V.
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective
16 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
Light coming from a discharge tube filled with hydrogen falls on the cathode of the photoelectric cell. The work function of the surface of cathode is 4eV Which one of the following values of the anode voltage (in volts ) with respect to the cathode willl likely to make the photoo current zero.
View SolutionThe work function for a metal is 4 eV. To eject the photo electrons with zero velocity the wavelength of the incident light should be
View SolutionThe work function for a metal is 40eV. To emit photo electrons of zero velocity from the surface of the metal the wavelength of incident light should be xnm.
View SolutionLight of wavelength λphfalls on a cathode plate inside a vacuum tube as shown in the figure .The work function of the cathode surface is ϕ and the anode is a wire mesh of conducting material kept at distance d from the cathode. A potential different V is maintained between the electrodes. If the minimum de Broglie wavelength of the electrons passing through the anode is λe which of the following statement (s) is (are) true?
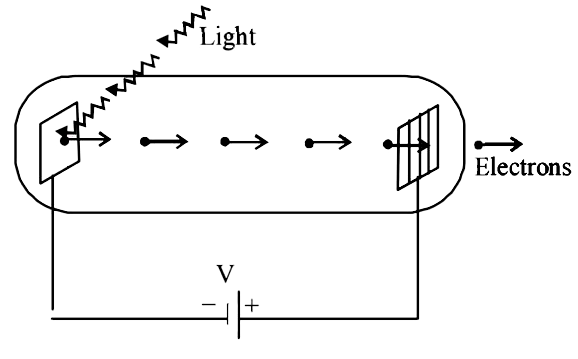
View SolutionThe work function for a metal is 4eV. To emit a photoelectron of
zero velocity from the surface of the metal, the wavelength of
incident light should be :
View SolutionThe work function for a metal is 4eV. To emit a photoelectron of zero velocity from the surface of the metal, the wavelength of incident light should be :
View SolutionMonochromatic light of wavelength 198 nm is incident on the surface of a metallic cathode whose work function is 2-5 eV. How muchpotential difference must be applied between the cathode and the anode of a photocell to just stop the photo current from flowing?
View SolutionPhotons with energy 5eV are incident on a cathode C in a photoelectric cell . The maximum energy of emitted photoelectrons is 2eV. When photons of energy 6eV are incident on C , no photoelectrons will reach the anode A , if the stopping potential of A relative to C is
View SolutionElectrons are emitted from the cathode of a photocell of negligible work function, when photons of wavelength λ are incident on it. Derive the expression for the de Broglie wavelength of the electrons emitted in terms of the wavelength of the incident light
View SolutionLight of wavelength 4000A∘ is incident on a metal surface. The maximum kinetic energy of emitted photoelectron is 2 eV. What is the work function of the metal surface?
View Solution
