Light from a point source in air falls on a spherical glass surface. If μ=1.5, and radius of curvature =20cm, the distance of light source from the glass surface is 100cm , at what position will the image be formed ? (NCERT Solved Example)
To solve the problem, we will use the formula for refraction at a spherical surface. The formula is:
μ2V−μ1U=μ2−μ1R
Where:
- μ1 is the refractive index of the medium from which light is coming (air in this case, μ1=1).
- μ2 is the refractive index of the medium into which light is entering (glass in this case, μ2=1.5).
- U is the object distance (the distance of the light source from the glass surface, which is given as 100cm).
- V is the image distance (which we need to find).
- R is the radius of curvature of the spherical surface (given as 20cm).
1. Identify the values:
- μ1=1 (for air)
- μ2=1.5 (for glass)
- R=20cm (radius of curvature)
- U=−100cm (the object distance is negative as per the sign convention)
2. Substitute the values into the formula:
1.5V−1−100=1.5−120
3. Simplify the equation:
1.5V+1100=0.520
1.5V+1100=0.025
4. Convert 1100 to a decimal:
1100=0.01
Thus, the equation becomes:
1.5V+0.01=0.025
5. Isolate 1.5V:
1.5V=0.025−0.01
1.5V=0.015
6. Solve for V:
V=1.50.015
V=100cm
Conclusion:
The image is formed at a distance of 100cm from the glass boundary.
- μ1 is the refractive index of the medium from which light is coming (air in this case, μ1=1).
- μ2 is the refractive index of the medium into which light is entering (glass in this case, μ2=1.5).
- U is the object distance (the distance of the light source from the glass surface, which is given as 100cm).
- V is the image distance (which we need to find).
- R is the radius of curvature of the spherical surface (given as 20cm).
- μ1=1 (for air)
- μ2=1.5 (for glass)
- R=20cm (radius of curvature)
- U=−100cm (the object distance is negative as per the sign convention)
1.5V−1−100=1.5−120
1.5V+1100=0.520
1.5V+1100=0.025
1100=0.01
Thus, the equation becomes:
1.5V+0.01=0.025
1.5V=0.025−0.01
1.5V=0.015
V=1.50.015
V=100cm
The image is formed at a distance of 100cm from the glass boundary.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise
32 Videos
- NUCLEIBOOK - NCERT ENGLISHCHAPTER - NUCLEIEXERCISE - Exercise
31 Videos
- SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSBOOK - NCERT ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSEXERCISE - Exercise
15 Videos
Similar Questions
Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20cm. The distance of light source from the glass surface is 100cm. At what position is the image formed ?
View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index μ. What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
View Solution
Knowledge Check
From a point source a light falls on a spherical glass surface (μ=1.5 and radius of curvature =10cm). The distance between point source and glass surface is 50cm. The position of image is
A25cmB50cmC100cmD150cmA double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
A22.86 same side of the objectB22.86 opposite side of the objectC44.89 same side of the objectD44.89 opposite side of the object.
A poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at
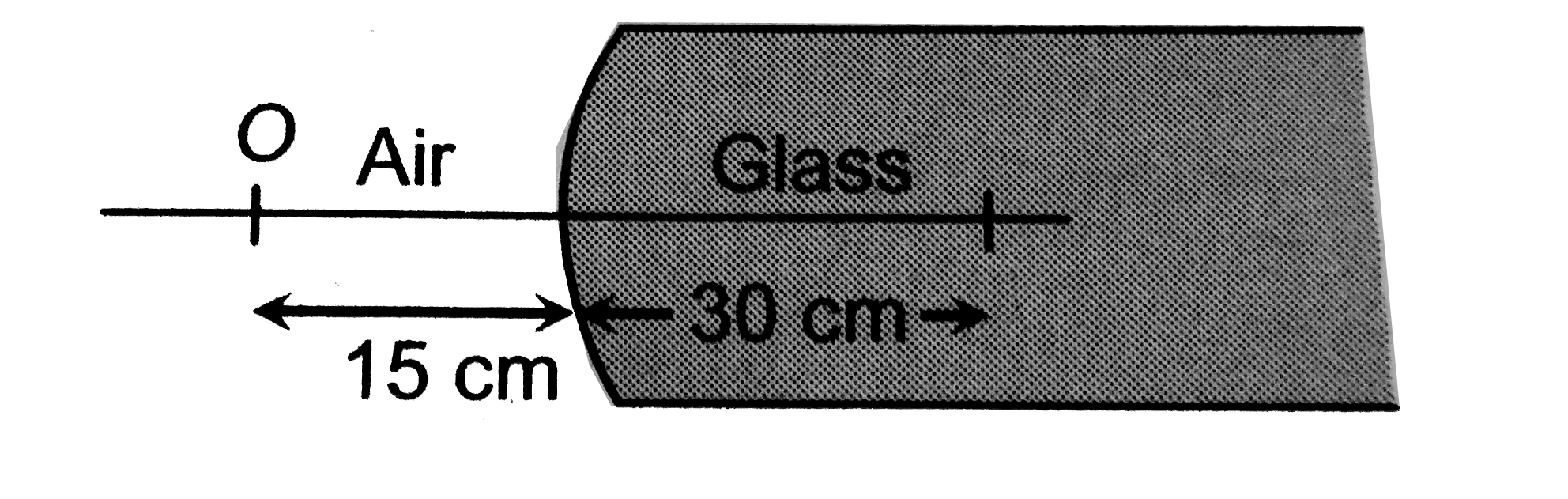
View SolutionA poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at

View SolutionA small object of height 0.5 cm is placed in front of a convex surface of glass (μ−1.5) of radius of curvature 10cm. Find the height of the image formed in glass.
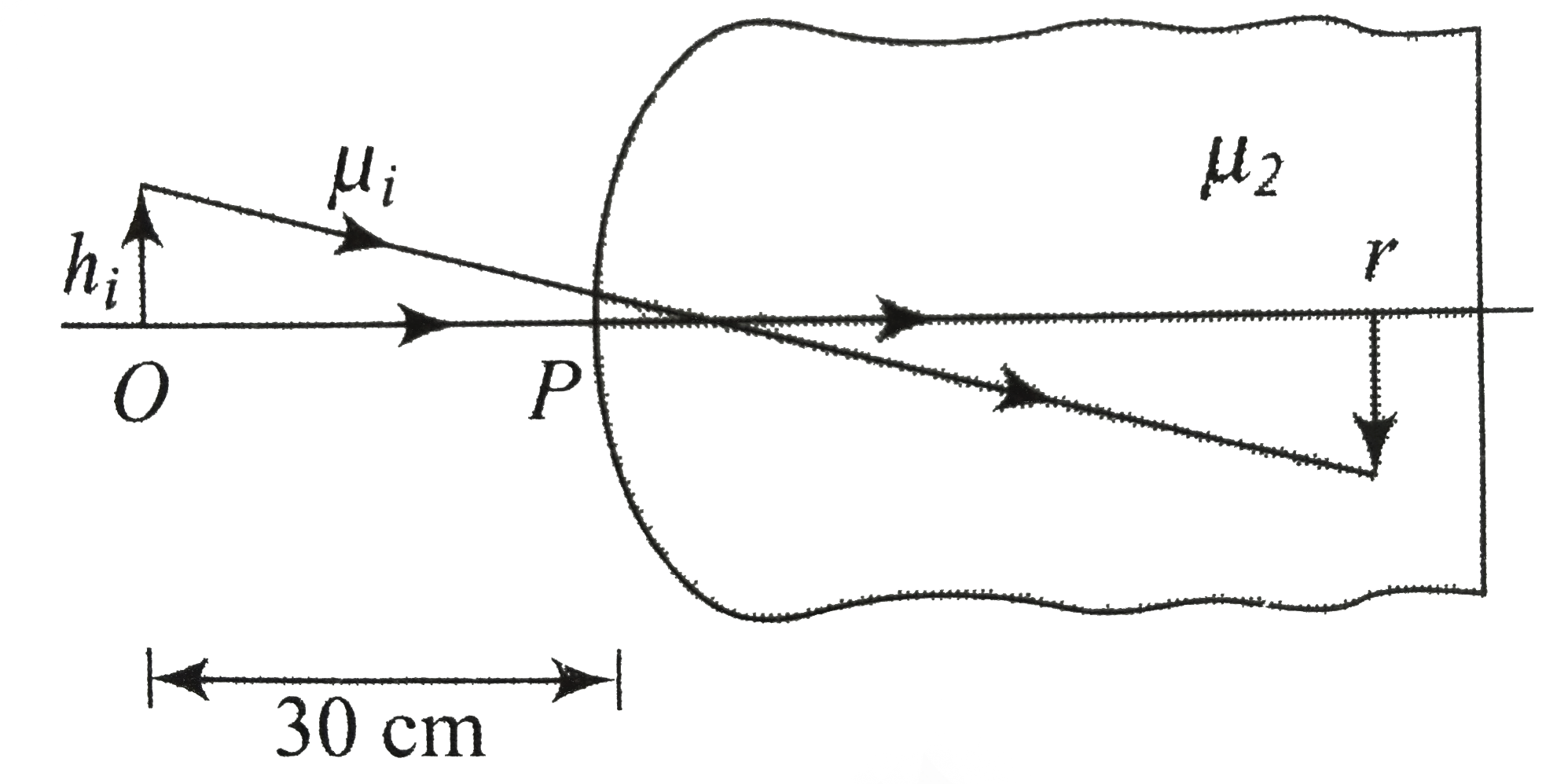
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View Solution
