(a) Fig. shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the axis of the pipe for which total reflection inside the pipe take place as shwon.
(b) What is the answer if there is no outer covering if the pipe ?
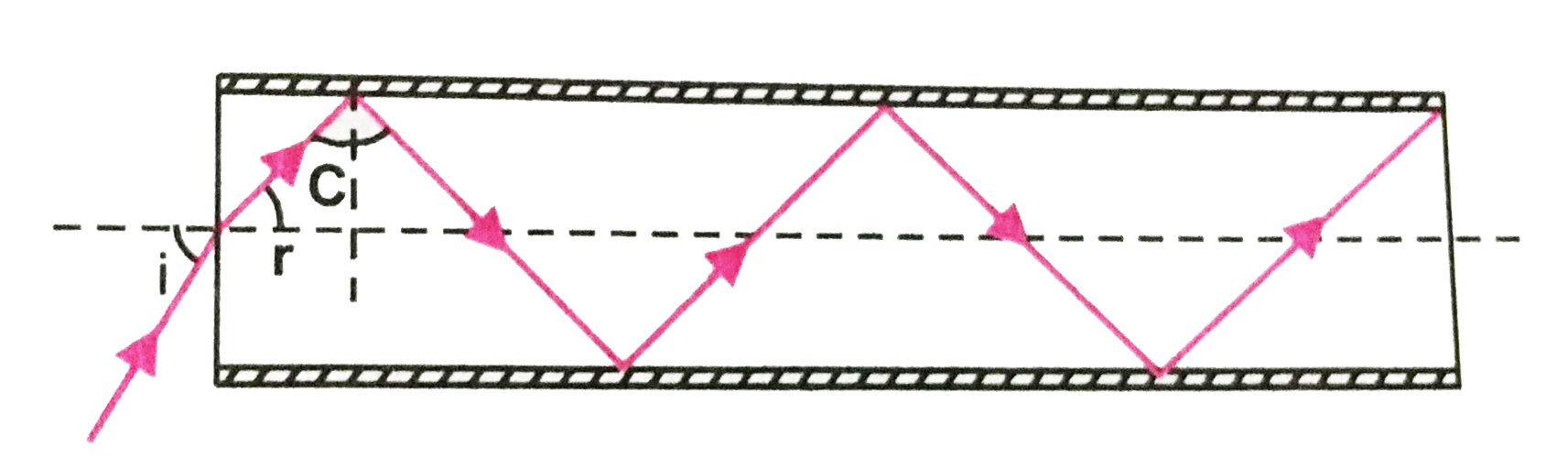
a) Refractive index of the glass fibre, μ1=1.68
Refractive index of the outer covering of the pipe, μ2=1.44
Angle of incidence =I
Angle of refraction =r
Angle of incidence at the interface =i′
The refractive index (μ) of the inner core-outer core interface is given as:
μ=μ2μ1=1sini
sini=μiμ2
−1.441.68=0.8571
∴i′=59∘.
For the critical angle, total internal reflection (TIR) takes place only when i>i′ , i.e., i>59∘.
Maximum angle of reflection, rmax=90∘−i′=90∘−59∘=31∘
Let, imax be the maximum angle of incidence.
The refractive index at the air-glass interface, μi=1.68
We have the relation for the maximum angles of incidence and reflection as:
μi=sinimaxsinrmax
sinimax=μisinrmax
=1.68sin31∘
=1.68×0.5150
=0.8652
∴imax=sin−10.8652≈60∘.
Thus, all the rays incident at angles inthe range 0<i<60∘.
thus, all the rays incident at angles lying in the range 0<i<60∘ will suffer total internal reflection.
b) If the outer covering of the pipe is not present, then,
Refractive index of the outer pipe, μi= Refractive index of air=1
For the angle of incidence i=90∘, we can write Snell's law at the air - pipe interface as:
sinisinr=μ2=1.68
sinr=sin90∘1.68=11.68
r=sin−1(0.p5952)
=36.5∘
∴i′=90∘−p36.5∘ = 53.5∘
Since, i′>r, all incident rays will suffer total internal reflection.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Exercise
32 Videos
- NUCLEIBOOK - NCERT ENGLISHCHAPTER - NUCLEIEXERCISE - Exercise
31 Videos
- SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSBOOK - NCERT ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS MATERIALS DEVICES AND SIMPLE CIRCUITSEXERCISE - Exercise
15 Videos
Similar Questions
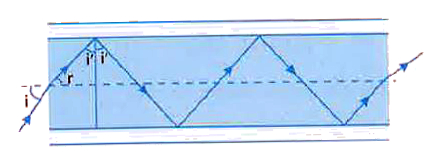
(a) Fig. 9.04 shows a cross-section of a Tight pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for which total reflections inside the pipe take place, as shown in the figure.
(b) What is the answer if there is no outer covering of the pipe ?
View Solution(a) Fig. shows a cross-section of a 'light pipe' made of a glass fibre of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the axis of the pipe for which total reflection inside the pipe take place as shwon.
(b) What is the answer if there is no outer covering if the pipe ?

View Solution
Knowledge Check
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, Fig. if :
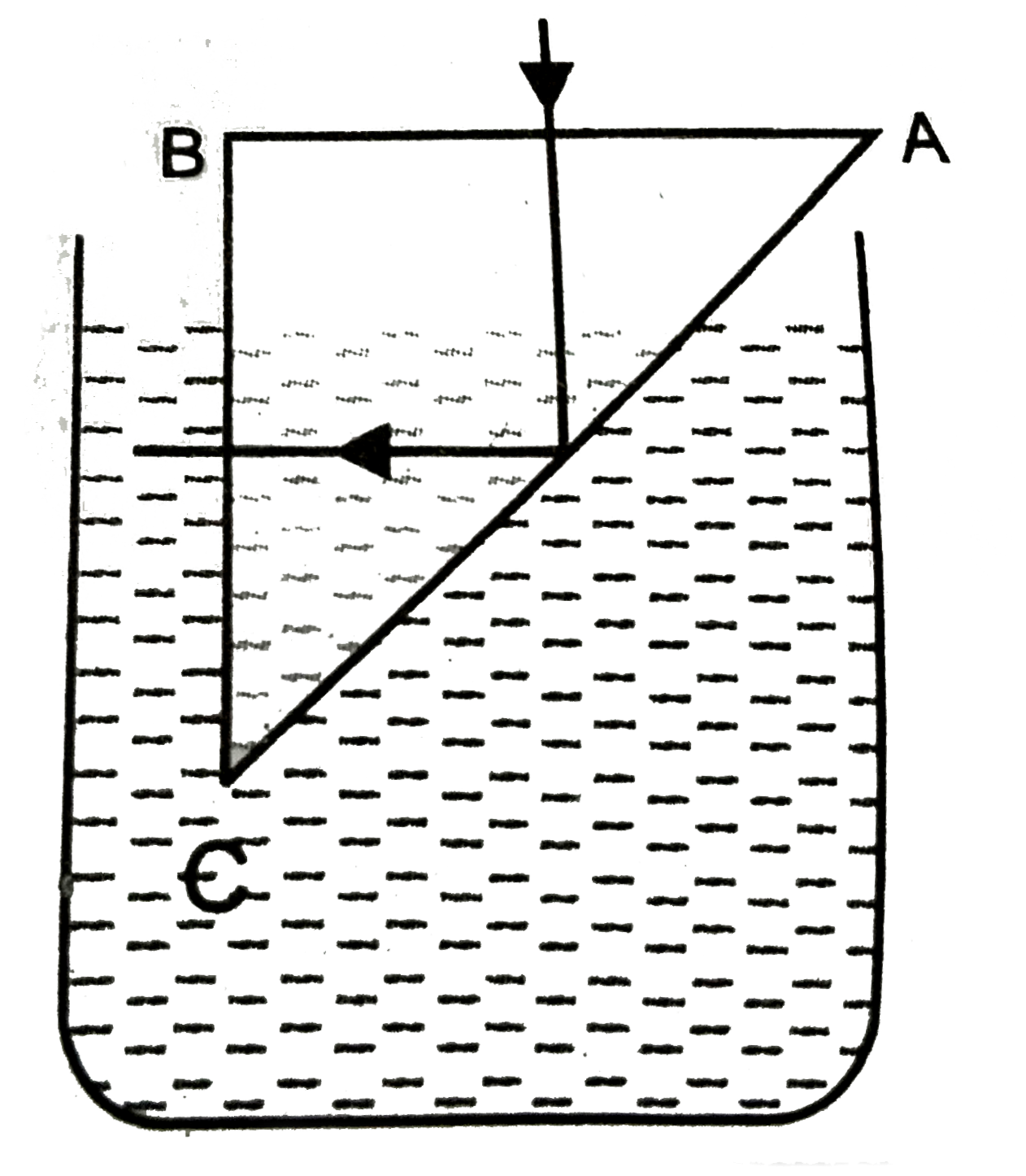 .AsinC=8/9BsinC=9/8CsinC=2/3DsinC=3/2
.AsinC=8/9BsinC=9/8CsinC=2/3DsinC=3/2In optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
A0.5653B0.6553C0.7653D0.8753In optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
A0.5653B0.6653C0.7653D08653
Cross section of a light pipe is shown in the following figure :

Inner core is material of refractive index 1.68 and its outer covering is a material of refractive index 1.44. Find the maximum angle at which the ray can be incident with the axis of pipe for which total internal reflection occurs inside the pipe.
View SolutionA ray of light falls on a transparent glass slab of refractive index 1.62. If the reflected ray and the refracted rays are mutually perpendicular, what is the angle of refraction ?
View SolutionA ray of light falls on a transparent glass slab of refractive index 1.62. If the reflected ray and the refracted rays are mutually perpendicular, what is the angle of refraction ?
View SolutionA thin convex lens made of material with refractive index 1.23 is placed in a medium with refractive index 1.56. What will be the nature of the lens now, converging or diverging ?
View SolutionIn optical fibre, refractive index of inner part is 1.68 and refractive index of outer part is 1.44. The numerical aperture of the fibre is
View Solution
