Light from a point source in air falls on a spherical glass surface. If μ=1.5, and radius of curvature =20cm, the distance of light source from the glass surface is 100cm , at what position will the image be formed ? (NCERT Solved Example)
25cm
50cm
100cm
200cm
The correct Answer is:C
To solve the problem, we will use the formula for refraction at a spherical surface. The formula is given by:
−n1u+n2v=n2−n1r
Where:
- n1 = refractive index of the first medium (air)
- n2 = refractive index of the second medium (glass)
- u = object distance
- v = image distance
- r = radius of curvature of the spherical surface
Step 1: Identify the given values
- Refractive index of air, n1=1
- Refractive index of glass, n2=1.5
- Radius of curvature, r=20cm
- Object distance, u=−100cm (negative as per sign convention)
Step 2: Substitute the values into the formula
Using the formula, we substitute the known values:
−1−100+1.5v=1.5−120
Step 3: Simplify the equation
This simplifies to:
1100+1.5v=0.520
Step 4: Calculate the right-hand side
Calculating the right-hand side:
0.520=0.025
So the equation now looks like:
1100+1.5v=0.025
Step 5: Isolate 1.5v
Now, we can isolate 1.5v:
1.5v=0.025−1100
Calculating 1100:
1100=0.01
So now we have:
1.5v=0.025−0.01=0.015
Step 6: Solve for v
Now, we can solve for v:
v=1.50.015
Calculating this gives:
v=100cm
Conclusion
The position of the image formed is at a distance of 100cm from the glass surface.
---
- n1 = refractive index of the first medium (air)
- n2 = refractive index of the second medium (glass)
- u = object distance
- v = image distance
- r = radius of curvature of the spherical surface
- Refractive index of air, n1=1
- Refractive index of glass, n2=1.5
- Radius of curvature, r=20cm
- Object distance, u=−100cm (negative as per sign convention)
Using the formula, we substitute the known values:
This simplifies to:
Calculating the right-hand side:
Now, we can isolate 1.5v:
Now, we can solve for v:
The position of the image formed is at a distance of 100cm from the glass surface.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Light from a point source in air falls on a convex spherical glass surface of refractive index 1.5 and radius of curvature 20cm. The distance of light source from the glass surface is 100cm. At what position is the image formed ?
View SolutionA parallel beam falls on solid glass sphere of radius R and refractive index μ. What is the distance of final image after refractioin from two surfaces of sphere? What is the condition for the image to be real?
View Solution
Knowledge Check
From a point source a light falls on a spherical glass surface (μ=1.5 and radius of curvature =10cm). The distance between point source and glass surface is 50cm. The position of image is
A25cmB50cmC100cmD150cmA double convex lens made of glass of refractive index 1.56 has both radii of curvature of magnitude 20cm. If an object is placed at a distance of 10cm from this lens, find the position of image formed.
A22.86 same side of the objectB22.86 opposite side of the objectC44.89 same side of the objectD44.89 opposite side of the object.
A poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at
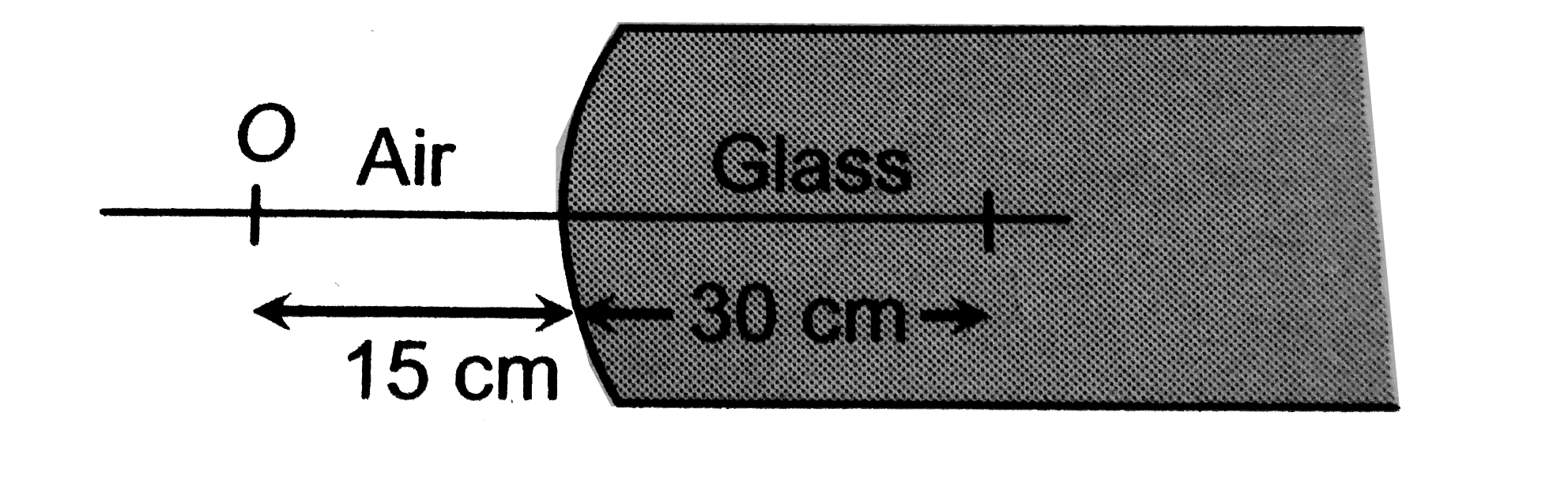
View SolutionA poinit object O is placed in front of a glass rod having spherical end of radius of curvature 30cm. The image would be formed at

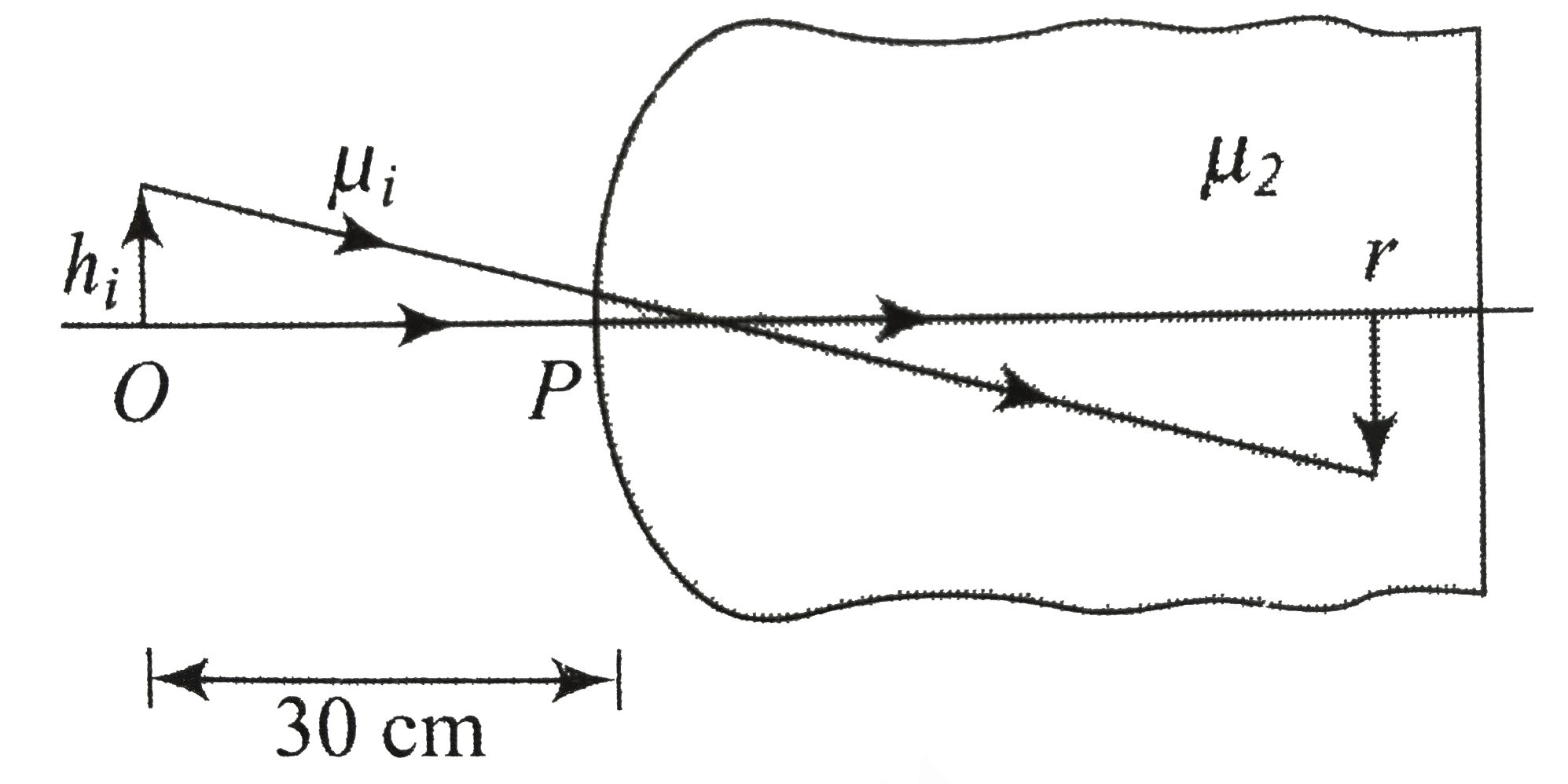
View SolutionA small object of height 0.5 cm is placed in front of a convex surface of glass (μ−1.5) of radius of curvature 10cm. Find the height of the image formed in glass.
View SolutionA point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
View SolutionA point object is placed at a distance 20 cm from the focus of a concave mirror of radius of curvature 20 cm. Find the distance (in cm) of the image from the focus.
View SolutionA concave mirror having a radius of curvature 40 cm is placed in front of an illuminated point source at a distance of 30 cm from it. Find the location of the image.
View Solution
