A convex lens of focal legnth 0.2m and made of glass (μ=1.50) is immersed in water (μ=1.33). Find the change in the focal length of the lens.
5.8m
0.58cm
0.58m
5.8cm
The correct Answer is:C
To find the change in the focal length of a convex lens when it is immersed in water, we can use the lens maker's formula. Here are the steps to solve the problem:
Step 1: Identify the given values
- Focal length of the lens in air, fA=0.2m
- Refractive index of the glass lens, μglass=1.50
- Refractive index of water, μwater=1.33
Step 2: Use the lens maker's formula in air
The lens maker's formula in air is given by:
1fA=(μglass−1)(1R1−1R2)
Where R1 and R2 are the radii of curvature of the lens surfaces.
Step 3: Calculate 1R1−1R2
From the formula, we can rearrange it to find 1R1−1R2:
1R1−1R2=1fA⋅1μglass−1
Substituting the known values:
1R1−1R2=10.2⋅11.50−1=10.2⋅10.5=10
Step 4: Use the lens maker's formula in water
Now, we apply the lens maker's formula when the lens is immersed in water:
1fW=(μglassμwater−1)(1R1−1R2)
Substituting the values:
1fW=(1.501.33−1)⋅10
Step 5: Calculate 1.501.33
Calculating 1.501.33:
1.501.33≈1.128
Thus,
1fW=(1.128−1)⋅10=0.128⋅10=1.28
Step 6: Calculate the focal length in water
Now, we find fW:
fW=11.28≈0.78125m
Step 7: Find the change in focal length
The change in focal length Δf is given by:
Δf=fW−fA=0.78125−0.2=0.58125m
Rounding this to two decimal places gives:
Δf≈0.58m
Final Answer
The change in the focal length of the lens when immersed in water is approximately 0.58 m.
---
- Focal length of the lens in air, fA=0.2m
- Refractive index of the glass lens, μglass=1.50
- Refractive index of water, μwater=1.33
The lens maker's formula in air is given by:
1fA=(μglass−1)(1R1−1R2)
Where R1 and R2 are the radii of curvature of the lens surfaces.
From the formula, we can rearrange it to find 1R1−1R2:
1R1−1R2=1fA⋅1μglass−1
Substituting the known values:
1R1−1R2=10.2⋅11.50−1=10.2⋅10.5=10
Now, we apply the lens maker's formula when the lens is immersed in water:
1fW=(μglassμwater−1)(1R1−1R2)
Substituting the values:
1fW=(1.501.33−1)⋅10
Calculating 1.501.33:
1.501.33≈1.128
Thus,
1fW=(1.128−1)⋅10=0.128⋅10=1.28
Now, we find fW:
fW=11.28≈0.78125m
The change in focal length Δf is given by:
Δf=fW−fA=0.78125−0.2=0.58125m
Rounding this to two decimal places gives:
Δf≈0.58m
The change in the focal length of the lens when immersed in water is approximately 0.58 m.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors
5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction
10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON
15 Videos
- PRACTICE PAPPERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 3
50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason
15 Videos
Similar Questions
A thin lens (μ=1.5) of focal length + 12 cm is immersed in water (μ=1.33). What is its new focal length ?
View SolutionA double convex lens of focal length 30 cm is made of glass. When it is immersed in a liquid of refractive index 1.4, the focal length is found to be 126 cm. The critical angle between glass and the liquid is
View Solution
Knowledge Check
A convex lens, made of glass, is immersed in water. As a result, its focal length will:
AincreaseBdecreaseCdoubleDremain same
One face of an equiconvex lens of focal length 60cm made of glass (μ=1.5) is silvered. Does it behave like a convex mirror or concave mirror? Determine its focal length.
View SolutionA biconvex lens of focal length 20cm, made of glass or refractive index 1.5, has water (μ=1.33) on one side and air on the other. An object is placed 15 cm form the lens on the side with water. Where is the image formed?
View Solution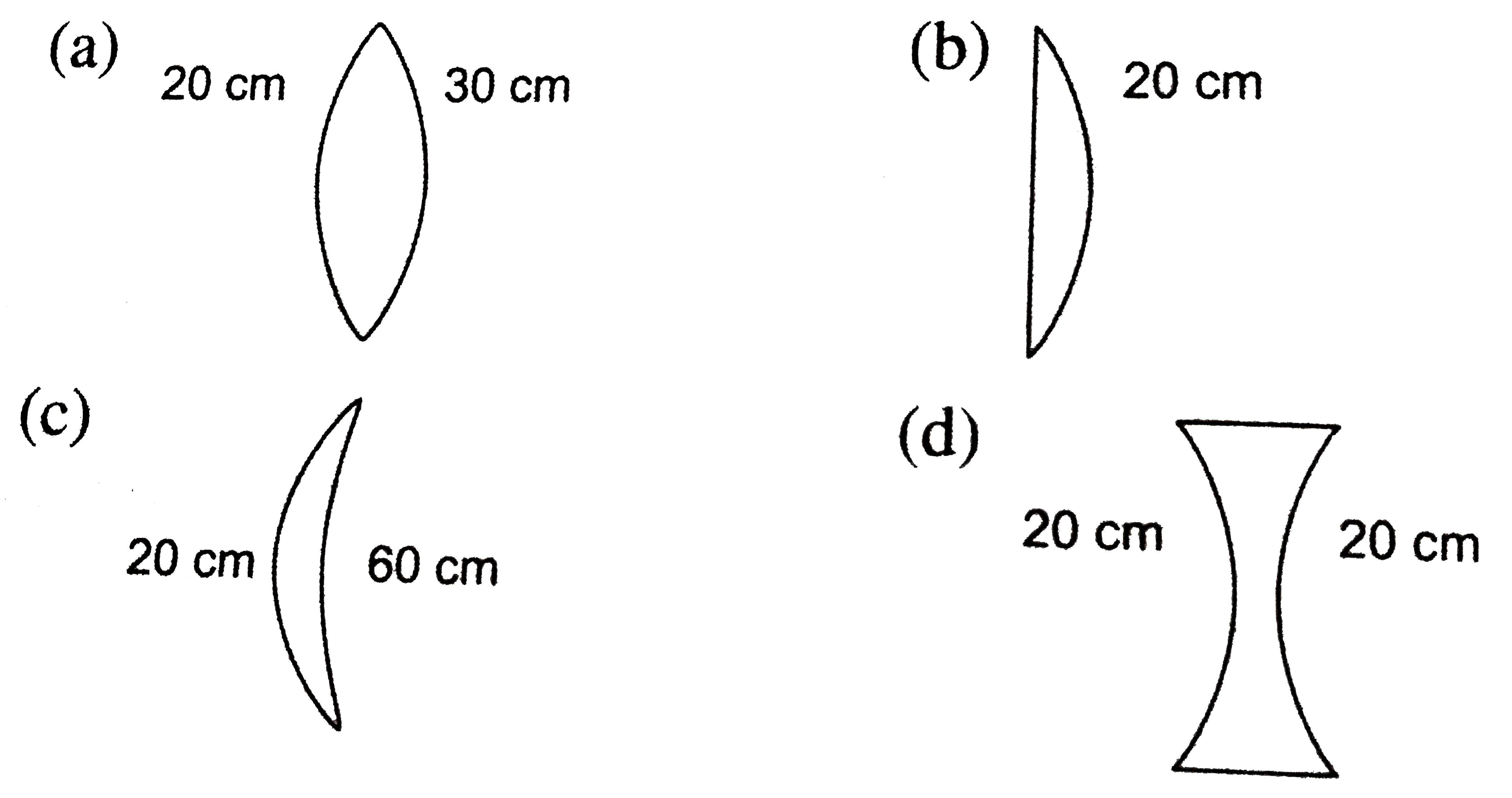
Find focal lengths of lenses made of glass (μ=3/2) and placed in air.
View SolutionA concave mirror of focal length f (in air) is immersed in water (μ=4/3). The focal length of the mirror in water will be
View SolutionA convex lens of focal length 12cm is made of glass of μ=32. What will be its focal length when immersed in liquid of μ=54 ?
View SolutionA thin lens made of glass of refractive index μ=1.5 has a focal length equal to 12 cm in air. It is now immersed in water (μ=43). Its new focal length is
View SolutionFocal length of convex lens in air is 16 cm (μglass=1.5). Now the lens is submerged in liquid of refractive index 1.42. Find the ratio of focal length in medium to focal length in air has closest value
View Solution
