Light of wavelength 5,000Å is used in a microscope of numerical aperture 0.10. Calculate the resovlving power of the microscope.
The correct Answer is:3.3×105m−1
To calculate the resolving power of the microscope, we can follow these steps:
Step 1: Understand the formula for resolving power
The resolving power R of a microscope is given by the formula:
R=2μsinθ1.22λ
where:
- μsinθ is the numerical aperture (NA) of the microscope,
- λ is the wavelength of light used.
Step 2: Identify the given values
From the problem, we have:
- Wavelength λ=5000 Å (angstroms),
- Numerical aperture μsinθ=0.10.
Step 3: Convert the wavelength to meters
Since the wavelength is given in angstroms, we need to convert it to meters:
λ=5000Å=5000×10−10m=5×10−7m.
Step 4: Substitute the values into the formula
Now, substituting the values into the resolving power formula:
R=2×0.101.22×5×10−7.
Step 5: Calculate the denominator
First, calculate the denominator:
1.22×5×10−7=6.1×10−7.
Step 6: Calculate the resolving power
Now substitute this back into the formula for R:
R=0.206.1×10−7.
Step 7: Perform the division
Calculating the division:
R=0.206.1×10−7=20×10−16.1×10−7=206.1×106≈3.2787×105m−1.
Step 8: Round the final answer
Rounding the answer gives:
R≈3.3×105m−1.
Final Answer
The resolving power of the microscope is approximately 3.3×105m−1.
---
The resolving power R of a microscope is given by the formula:
R=2μsinθ1.22λ
where:
- μsinθ is the numerical aperture (NA) of the microscope,
- λ is the wavelength of light used.
From the problem, we have:
- Wavelength λ=5000 Å (angstroms),
- Numerical aperture μsinθ=0.10.
Since the wavelength is given in angstroms, we need to convert it to meters:
λ=5000Å=5000×10−10m=5×10−7m.
Now, substituting the values into the resolving power formula:
R=2×0.101.22×5×10−7.
First, calculate the denominator:
1.22×5×10−7=6.1×10−7.
Now substitute this back into the formula for R:
R=0.206.1×10−7.
Calculating the division:
R=0.206.1×10−7=20×10−16.1×10−7=206.1×106≈3.2787×105m−1.
Rounding the answer gives:
R≈3.3×105m−1.
The resolving power of the microscope is approximately 3.3×105m−1.
Topper's Solved these Questions
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - PRACTICE PROBLEMS (4)
9 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - Conceptual Questions
23 Videos
- WAVE OPTICALBOOK - MODERN PUBLICATIONCHAPTER - WAVE OPTICALEXERCISE - PRACTICE PROBLEMS (2)
10 Videos
- SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS BOOK - MODERN PUBLICATIONCHAPTER - SEMICONDUCTOR ELECTRONICS METERIALS DEVICES AND SIMPLE CIRCUITS EXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION
12 Videos
Similar Questions
Light of wavelength 5,000Å is falling on a microscope objective lens with a cone angle of 60∘. Calculate the resolving power of the microscope.
View SolutionWhen an object is viewed with a light of wavelength 6000Å under a microscope, its resolving power is 104. The resolving power of the microscope when the same object is viewed with a light of wavelength 4000Å, is n×103. The vlaue of n is
View Solution
Knowledge Check
Resolving power of light microscope is
A0.2μmB0.1μmC2μmD100μmWhich colour should be used to increases the resolving power of a microscope
AvioletBredCyellowDgreenA telescope uses light having wavelength 5000 Å and aperture of the objective is 10 cm, then the resolving limit and magnifying power of the telescope is respectively
A6.1×10−6 rad and 12B5.0×10−6 rad and 12C6.1×10−6 rad and 8.3×10−2D5.0×10−6 rad and 8.3×10−2
When an object is viewed with a light of wavelength 6000Å under a microscope, its resolving power is 104. The resolving power of the microscope when the same object is viewed with a light of wavelength 4000Å, is n×103. The vlaue of n is
View SolutionThe numerical aperture of a microscope is 0.31. If the wavelength of light used in 600 nm, calculate the resolving power of the microscope.
View SolutionAn oil immersion microscope can just resolve two point objects separated by 0.6 m, when light of wavelength 485 nm is used for illumination. If the semi vertical angle is 20∘, calculate the refractive index of the oil used and resolving power of the microscope.
View SolutionA thin convex lens of focal length 5 cm is used as a simple microscope by a person with normal near point (25 cm). What is the magnifying power of the microscope ?
View SolutionIn a modified Young's double slit experiment a monochromatic uniform and parallel beam of light of wave length 6000Å and intensity (10π)Wm−2 is incident normally on two circular apertures A and B of radii 20009Å and refractive index 1.5 for the wavelength of 6000Å is placed in front of aperture. A. Calculate the power (in watt) received at the focal spot F of the lens. The lens is symmertrically placed with respect to the apertures. Assume that 10% of the power received by each aperture goes in the originally direction and is brought to the focal spot.
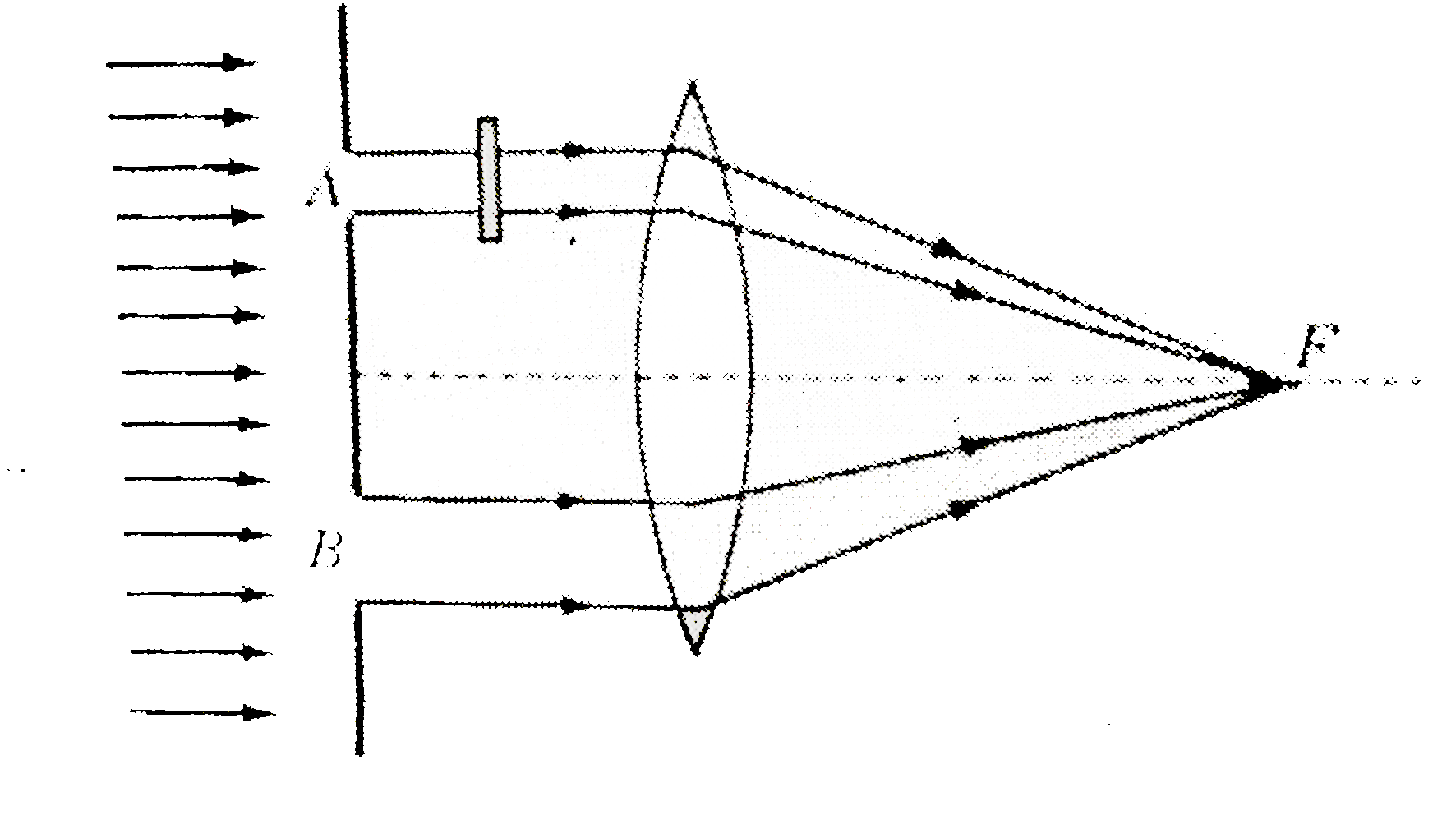
View Solution
