Light of wavelength λ falls on metal having work functions hc/λ0 . Photoelectric effect will take place only if :
λ≥(λ0)
λ≥2λ0
λ≤λ0
λ<λ02
The correct Answer is:C
To solve the question, we need to determine the condition under which the photoelectric effect occurs when light of wavelength λ falls on a metal with a work function given by hcλ0.
1. Understand the Work Function: The work function (φ₀) is the minimum energy required to eject an electron from the metal surface. In this case, it is given as:
\(
\phi_0 = \frac{hc}{\lambda_0}
\)
where h is Planck's constant, c is the speed of light, and λ₀ is a specific wavelength related to the work function.
2. Photon Energy Calculation: The energy (E) of a photon with wavelength λ is given by the formula:
\(
E = \frac{hc}{\lambda}
\)
3. Condition for Photoelectric Emission: For the photoelectric effect to occur, the energy of the incident photon must be greater than or equal to the work function:
\(
E \geq \phi_0
\)
Substituting the expressions for E and φ₀, we get:
\(
\frac{hc}{\lambda} \geq \frac{hc}{\lambda_0}
\)
4. Simplifying the Inequality: We can cancel hc from both sides (assuming hc is not zero):
\(
\frac{1}{\lambda} \geq \frac{1}{\lambda_0}
\)
5. Reciprocal of the Inequality: Taking the reciprocal of both sides reverses the inequality:
\(
\lambda \leq \lambda_0
\)
6. Conclusion: The condition for the photoelectric effect to take place is that the wavelength λ must be less than or equal to λ0.
Final Answer:
The photoelectric effect will take place only if:
\(
\lambda \leq \lambda_0
\)
\(
\phi_0 = \frac{hc}{\lambda_0}
\)
where h is Planck's constant, c is the speed of light, and λ₀ is a specific wavelength related to the work function.
\(
E = \frac{hc}{\lambda}
\)
\(
E \geq \phi_0
\)
Substituting the expressions for E and φ₀, we get:
\(
\frac{hc}{\lambda} \geq \frac{hc}{\lambda_0}
\)
\(
\frac{1}{\lambda} \geq \frac{1}{\lambda_0}
\)
\(
\lambda \leq \lambda_0
\)
The photoelectric effect will take place only if:
\(
\lambda \leq \lambda_0
\)
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective II
7 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - Exercise
35 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - work out
13 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
The work function of a metal is hv0. Light of frequency v falls on this metal. The photoelectric effect will take place only if
View SolutionA metal has a work function ϕ0 and its corresponding threshold wavelength is λ0. If the threshold wavelength for a metal whose work function is ϕ03 is nλ0, then what is the value of n ?
View SolutionThe graph between 1/λ and stopping potential (V) of three metals having work- functions Φ1, Φ2 and Φ3 in an experiment of photoelectric effect is plotted as shown in the figure. Which of the following statement(s) is/are correct? (Here, λ is the wavelength of the incident ray).
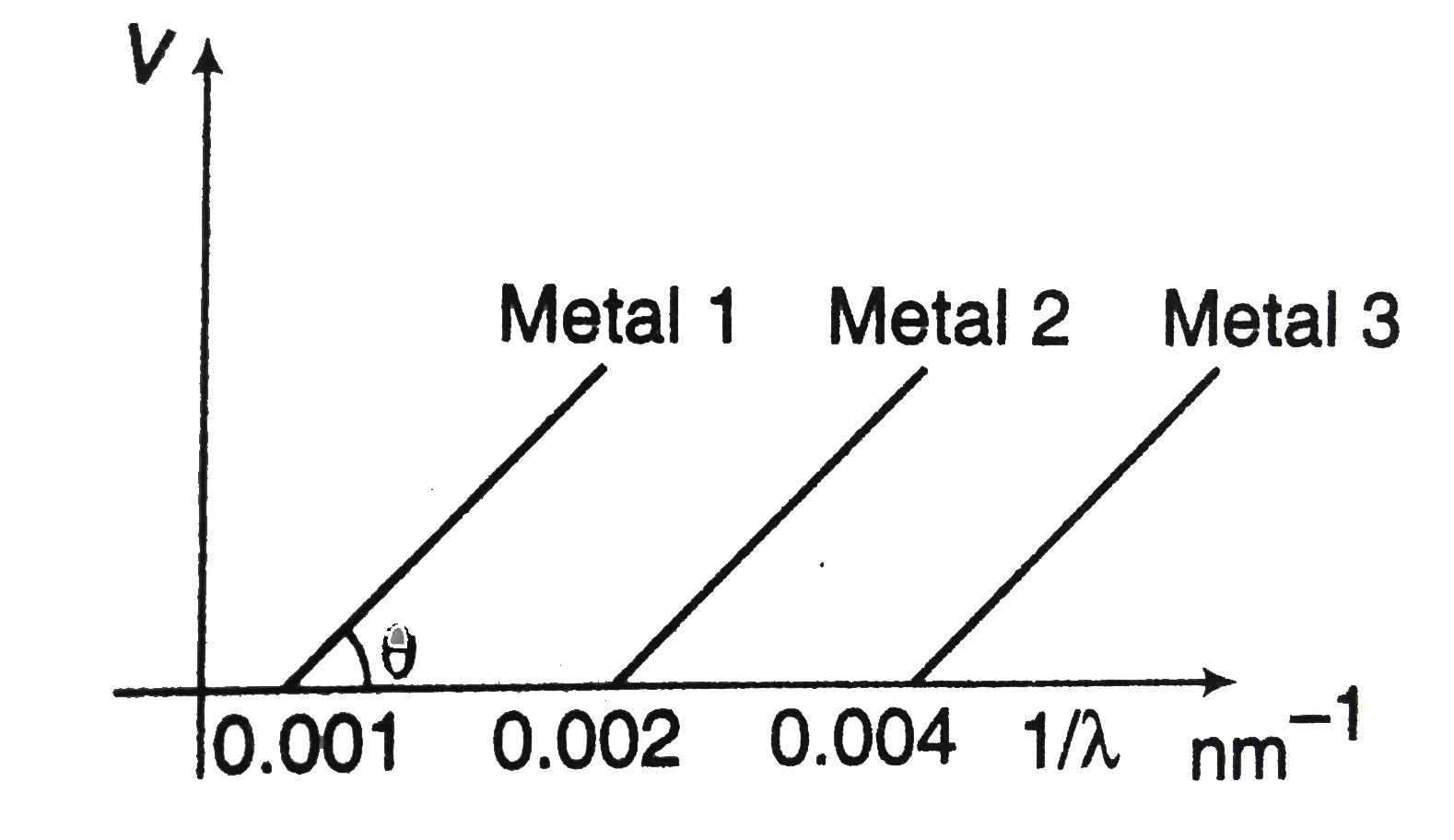
View SolutionLight of wavelength λ is incident on metal surface. Work function of metal is very small compare to kinetic energy of photon. If light of wave length λ' is incident on metal surface then linear momentum of electron becomes 1.5 of initial, find out λ'.
View SolutionLight of wavelength 2000 Å falls on a metallic surface whose work function is 4.21 eV. Calculate the stopping potential
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV . The stopping potential is
View SolutionIf light of wavelength λ1 is allowed to fall on a metal , then kinetic energy of photoelectrons emitted is E1. If wavelength of light changes to λ2 then kinetic energy of electrons changes to E2. Then work function of the metal is
View SolutionIf the threshold wavelength (λ0) for ejection of electron from metal is 330 nm, then work function for the photoelectric emission is:
View SolutionThe maximum velocity of an electron emitted by light of wavelength λ incident on the surface of a metal of work function ϕ, is
Where h = Planck's constant , m = mass of electron and c = speed of light.
View SolutionWhen light of wavelength λ is incident on a metal surface, stopping potential is found to be x. When light of wavelength nλ is incident on the same metal surface, stopping potential is found to be xn+1 . Find the threshold wavelength of the metal.
View Solution
