Light of wavelength from a small 0.5 mW He-Ne laser source, used in the school laboratory, shines from a spacecraft of mass 1000 kg. Estimate the time needed for the spacecraft to reach a velocity of from rest. The momentum p of a photon of wavelength is given by , where h is Planck's constant.
The correct Answer is:C
To solve the problem step by step, we can follow these calculations:
Step 1: Calculate the Energy Emitted by the Laser
The power of the laser is given as P=0.5mW=0.5×10−3W.
Step 2: Calculate the Number of Photons Emitted per Second
The energy of a single photon is given by the equation:
E=hcλ
where:
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength of the light.
The number of photons emitted per second, N, can be calculated using the formula:
N=PE=Pλhc
Step 3: Calculate the Momentum of a Photon
The momentum p of a photon is given by:
p=hλ
Step 4: Calculate the Rate of Change of Momentum
The total momentum imparted to the spacecraft per second (which is the force) is given by:
F=Np=N(hλ)
Substituting N from Step 2:
F=(Pλhc)(hλ)=Pc
Step 5: Relate Force to Acceleration
Using Newton's second law, we can relate the force to the acceleration a:
F=ma
where m=1000kg (mass of the spacecraft). Thus,
a=Fm=Pmc
Step 6: Calculate the Acceleration
Substituting the values:
a=0.5×10−31000×3×108=0.5×10−33×1011=0.53×10−14m/s2
a≈1.67×10−15m/s2
Step 7: Calculate the Time to Reach the Desired Velocity
Using the equation of motion:
v=u+at
Since the spacecraft starts from rest, u=0:
v=at⟹t=va
Substituting v=1km/s=1000m/s:
t=10001.67×10−15≈5.99×1017s
Final Answer
The time needed for the spacecraft to reach a velocity of 1.0km/s from rest is approximately 5.99×1017 seconds.
---
The power of the laser is given as P=0.5mW=0.5×10−3W.
The energy of a single photon is given by the equation:
E=hcλ
where:
- h is Planck's constant (6.626×10−34Js),
- c is the speed of light (3×108m/s),
- λ is the wavelength of the light.
N=PE=Pλhc
The momentum p of a photon is given by:
p=hλ
The total momentum imparted to the spacecraft per second (which is the force) is given by:
F=Np=N(hλ)
Substituting N from Step 2:
F=(Pλhc)(hλ)=Pc
Using Newton's second law, we can relate the force to the acceleration a:
F=ma
where m=1000kg (mass of the spacecraft). Thus,
a=Fm=Pmc
Substituting the values:
a=0.5×10−31000×3×108=0.5×10−33×1011=0.53×10−14m/s2
a≈1.67×10−15m/s2
Using the equation of motion:
v=u+at
Since the spacecraft starts from rest, u=0:
v=at⟹t=va
Substituting v=1km/s=1000m/s:
t=10001.67×10−15≈5.99×1017s
The time needed for the spacecraft to reach a velocity of 1.0km/s from rest is approximately 5.99×1017 seconds.
Topper's Solved these Questions
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Multiple Correct
10 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Linked Comprehension
44 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Subjective
16 Videos
- NUCLEAR PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.5
14 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
Similar Questions
A chemist was performing an experiment to study the effect of varying voltage and de-Broglie wavelength of the electron. In first experiment, the electron was accelerated through a potential difference of 1 kV from rest and in second experiment, it was accelerated through a potential difference of 2 kV from rest. The wavelength of de-Broglie waves associated with electron is given by
λ=h√2qVm
Where, V is the voltage through which one electron is accelerated
Putting the values of h, m and q, we get
λ=12.3√VÅ
Answer the following question
In order of get half velocity of electron than in second case , the applied potential difference from rest will be :
View SolutionA laser light of wavelength 660 nm is used to weld Retina detachment. If a laser pulse of width 60 ms and power 0.5 kW is used, the approximate number of photons in the pulse are (Take Planck's Constant, h=6.62×10−34Js)
View Solution
Knowledge Check
Light of wavelength 0.6μmfrom a sodium lamp falls on a photocell and causes the emission of photoelectrons for which the stopping potential is 0.5 V. With wavelength 0.4μm from a sodium lamp, the stopping potential is 1.5 V. With this data , the value of h/e is
A4×10−59VsB0.25×10−15VsC10×10−15VsD4×10−8Vs.A car starts from rest, attain a velocity of 36kmh−1 with an acceleration of 0.2ms−2, travels 9 km with this uniform velocity and then comes to halt with a uniform deaceleration of 0.1 ms−2. The total time of travel of the car is
A1050 sB1000 sC950 sD900 s
de Broglie (1924) predicted that small particles such as electrons should show wave -like properties along with paticle character. The wave length(λ) associated with particle of mass m and moving with velocity v is given as λ=hmv where 'h' is plank's constant. The wave nature was confirmed by Davisson and Germer's experiment and modified equation for calculation of λ can be given as:
λ=−h√2Em where E= kinetic energy of particle.
λ=h√2dVm, where d= change of particle accelerated potnetial of V volt.
The ratio of de-Broglie χ wavelength of molecules of H2 and He at 27∘C adn 127∘C respectively is
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght λ1=550nm is incident on it. The stopping potential for such electrons is λS1=0.19V. Suppose that radiation of wavelength λ2=190nm is incident of the surface.
Q. Calculate the stopping potential VS2.
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght λ1=550nm is incident on it. The stopping potential for such electrons is λS1=0.19V. Suppose that radiation of wavelength λ2=190nm is incident of the surface.
Q. Calulate the work function of the surface.
View SolutionA photon of wavelength 400nm strikes a metal surface. The electrons are ejected with a velocity 5.85×105ms−1. Calculate the minimum energy required to remove an electron from the metal surface. The mass of an electron is 9.109×10−31kg.
View SolutionGive the magnitude and direction of the force acting on a stone of mass 0.1 kg (a) just after it is dropped from the window of a stationary train
(b) just after it is dropped from the window of a train running at a constant velocity of 36km/hr
(c) just after it is dropped from the window of a train accelerating with 1ms−2
(d) lying on the floor of a train which is accelerating with 1ms−2 the stone being at rest relative to the train .
Neglect the resistance of air throughout .
View SolutionHydrogen is the simplest atom of nature. There is one proton in its nucleus and an electron moves around the nucleus in a circular orbit. According to Niels Bohr's, this electron moves in a stationary orbit, if emits no electromagnetic radiation. The angular momentum of the electron is quantized , i.e., mvr=(nh/2π), where m= mass of the electron , v=velocity of the electron in the orbit , r=radius of the orbit , and n=1,2,3.... When transition takes place from Kth orbit to Jth orbit, energy photon is emitted. If the wavelength of the emitted photon is λ.
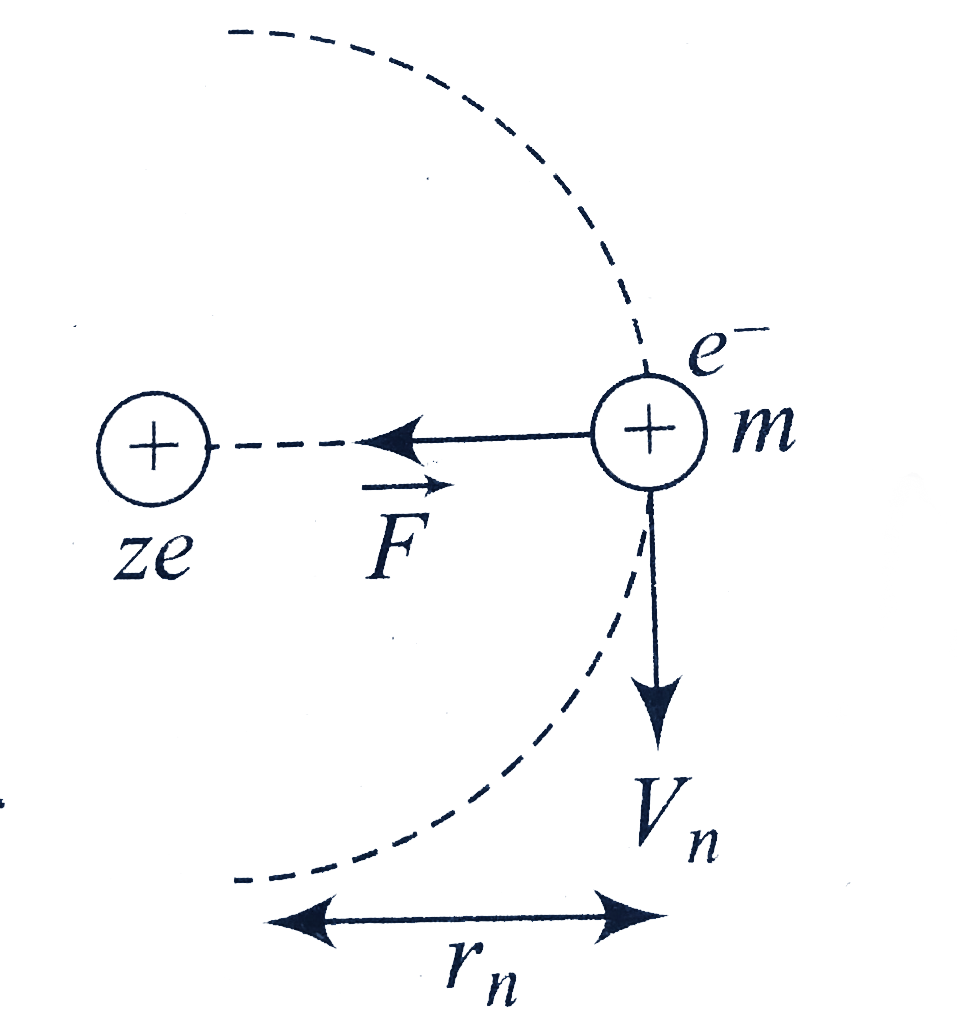
we find that 1λ=R[1J2−1K2], where R is
Rydberg's constant.
On a different planed, the hydrogen atom's structure was somewhat different from ours. The angular momentum of electron was P=2n(h/2π). i.e., an even multipal of (h/2π).
Answer the following questions regarding the other planet based on above passage:
In our world, the velocity of electron is v0 when the hydrogen atom is in the ground state on the other planet should be
View Solution
