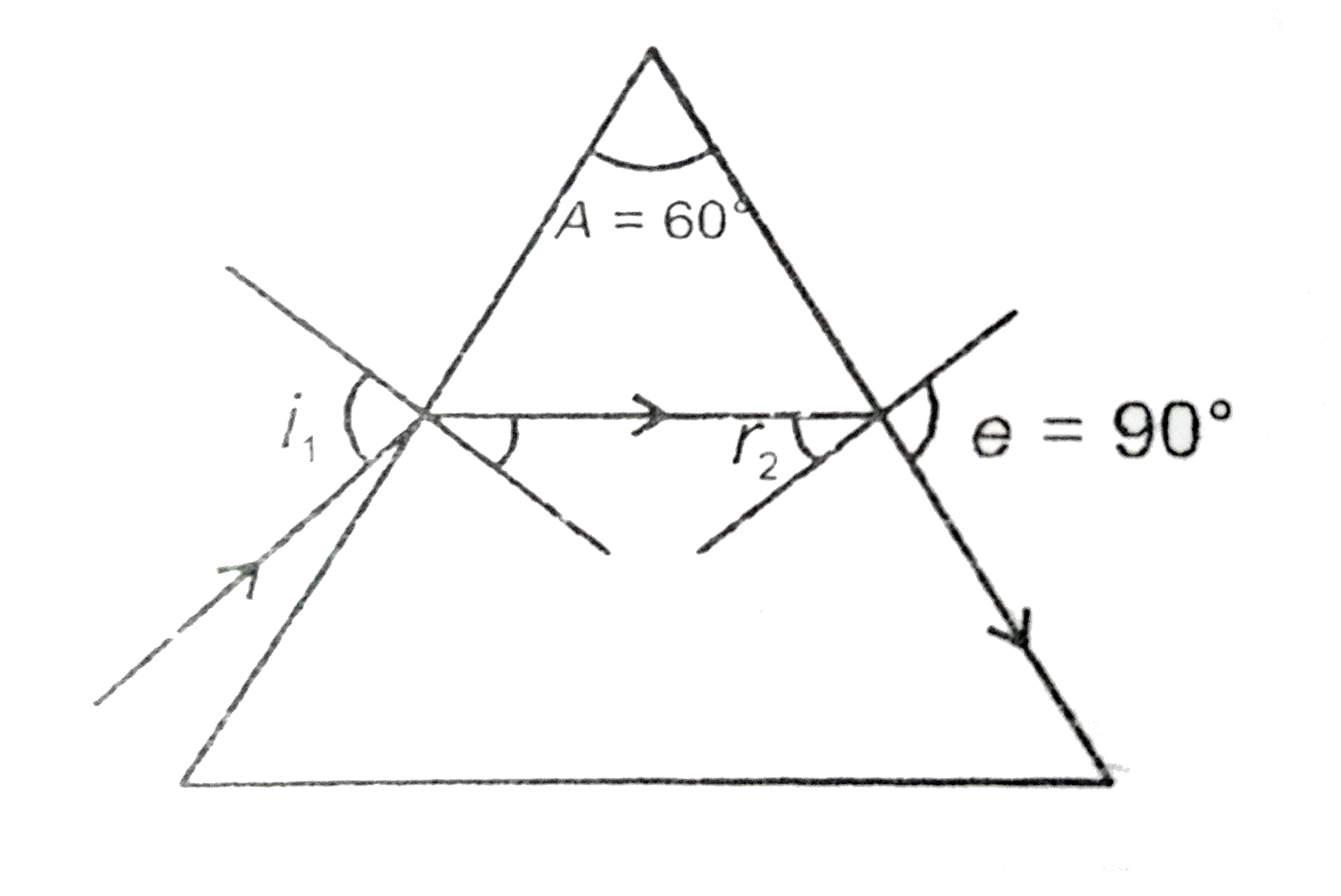
Light ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
sin−1(√3−12)
sin−1(√2−12)
sin−1(√32)
sin−1(23√3)
The correct Answer is:A
To solve the problem, we need to find the angle of incidence i for a light ray incident on a prism with an angle A=60∘ and a refractive index μ=√2, such that the emergent ray grazes the surface of the prism.
1. Understanding the Emergent Ray Condition:
Since the emergent ray grazes the surface, the angle of emergence E is 90∘.
2. Using Snell's Law at the Emergent Surface:
According to Snell's law at the second surface of the prism:
μ⋅sin(r2)=sin(E)
Here, E=90∘, so sin(90∘)=1. Therefore:
μ⋅sin(r2)=1
Substituting μ=√2:
√2⋅sin(r2)=1
This gives:
sin(r2)=1√2⟹r2=45∘
3. Relating Angles in the Prism:
In a prism, the angles are related by:
r1+r2=A
Substituting A=60∘ and r2=45∘:
r1+45∘=60∘
Therefore:
r1=60∘−45∘=15∘
4. Applying Snell's Law at the First Surface:
Now, we apply Snell's law at the first surface:
sin(i)=μ⋅sin(r1)
Substituting μ=√2 and r1=15∘:
sin(i)=√2⋅sin(15∘)
5. Calculating sin(15∘):
We can use the sine subtraction formula:
sin(15∘)=sin(45∘−30∘)=sin(45∘)cos(30∘)−cos(45∘)sin(30∘)
Knowing sin(45∘)=√22, cos(30∘)=√32, cos(45∘)=√22, and sin(30∘)=12:
sin(15∘)=√22⋅√32−√22⋅12=√64−√24=√6−√24
6. Substituting Back:
Now substituting sin(15∘) back into the equation for sin(i):
sin(i)=√2⋅√6−√24=√2(√6−√2)4
7. Finding the Angle of Incidence:
Finally, we find i:
i=sin−1(√2(√6−√2)4)
Final Answer:
The angle of incidence i is given by:
i=sin−1(√2(√6−√2)4)
Since the emergent ray grazes the surface, the angle of emergence E is 90∘.
According to Snell's law at the second surface of the prism:
μ⋅sin(r2)=sin(E)
Here, E=90∘, so sin(90∘)=1. Therefore:
μ⋅sin(r2)=1
Substituting μ=√2:
√2⋅sin(r2)=1
This gives:
sin(r2)=1√2⟹r2=45∘
In a prism, the angles are related by:
r1+r2=A
Substituting A=60∘ and r2=45∘:
r1+45∘=60∘
Therefore:
r1=60∘−45∘=15∘
Now, we apply Snell's law at the first surface:
sin(i)=μ⋅sin(r1)
Substituting μ=√2 and r1=15∘:
sin(i)=√2⋅sin(15∘)
We can use the sine subtraction formula:
sin(15∘)=sin(45∘−30∘)=sin(45∘)cos(30∘)−cos(45∘)sin(30∘)
Knowing sin(45∘)=√22, cos(30∘)=√32, cos(45∘)=√22, and sin(30∘)=12:
sin(15∘)=√22⋅√32−√22⋅12=√64−√24=√6−√24
Now substituting sin(15∘) back into the equation for sin(i):
sin(i)=√2⋅√6−√24=√2(√6−√2)4
Finally, we find i:
i=sin−1(√2(√6−√2)4)
The angle of incidence i is given by:
i=sin−1(√2(√6−√2)4)
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - A. Only one option is correct (JEE Advance)73videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct20videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer8videos
PROPERTIES OF MATTER
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
Similar Questions
A prism of apex angle A=60∘ has the refractive index μ=√2. The angle of incidence for minimum deviation is
View SolutionCalculate the angle of incidence on the face of a prism of refracting angle 60∘ and of refractive index 1.5, for which the emergent ray just grazes the other face.
 View Solution
View SolutionA light ray is incident on a transparent slab of refractive index μ=√2 at an angle of incidence π/4. Find the ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered.
View SolutionA ray of light is incident normally normallyh on one of the faces of a prism of apex angle 30∘ and refractive index √2. The angle of deviation of the ray is ________________ degrees.
View SolutionA ray of light is incident normally on one of the faces of a prism of apex angle 30 degree and refractive index √2. The angle of deviation of the ray in degrees is
View SolutionThe angle of a prism is 60∘ When light is incident at an angle of 60∘ on the prism, the angle of emerge is 40∘. The angle of incidence i for which the light ray will deviate the least is such that
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionAray of light falls on one side of a prism whose refracting angle is 75∘. Find the angle of incidence in order that the emergent ray may just graze the other side, (μ=√2)
View SolutionA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
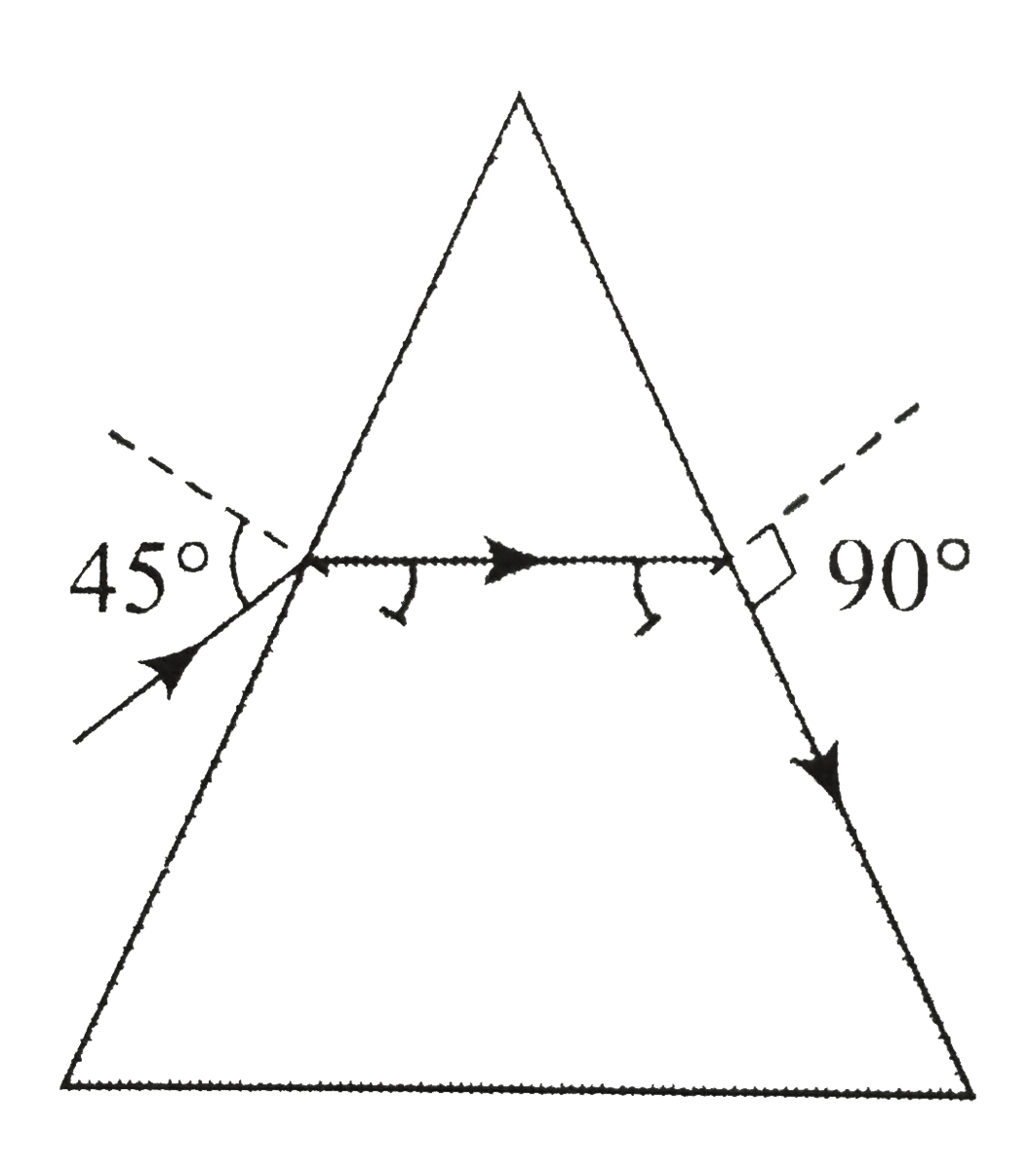
View SolutionIn an isosceles prism of angle 45∘, it is found that when the angle of incidence is same as the prism angle, the emergen ray grazes the emergent surface.
Find the refractive index of the material of the prism. For what angle of incidenc, the angle of deviation will be minimum?
 View Solution
View Solution

