A ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
tθ(n−1)n
tθn
tθnn−1
tθ(n+1)n
The correct Answer is:A
To find the lateral displacement of a ray of light passing through a parallel slab of thickness t and refractive index n when the angle of incidence θ is small, we can follow these steps:
1. Understanding the Geometry:
- Consider a parallel slab of thickness t and refractive index n.
- A ray of light strikes the slab at an angle θ (the angle of incidence).
2. Refraction at the Slab:
- When the ray enters the slab, it bends towards the normal due to the higher refractive index of the slab compared to air.
- Let R be the angle of refraction in the slab.
3. Using Snell's Law:
- According to Snell's Law:
n1sinθ=n2sinR
- Here, n1=1 (refractive index of air) and n2=n (refractive index of the slab).
- Thus, we have:
sinθ=nsinR
- For small angles, we can approximate sinθ≈θ and sinR≈R.
4. Finding R:
- From the equation sinθ=nsinR, we can express sinR:
sinR=sinθn≈θn
5. Calculating Lateral Displacement:
- The lateral displacement D can be calculated using the formula:
D=tcosR(sinθ−sinR)
- For small angles, cosR≈1 and sinR≈θn:
D≈t(θ−θn)
- Simplifying this gives:
D≈tθ(1−1n)
6. Final Expression for Lateral Displacement:
- Therefore, the lateral displacement D is:
D=tθ(n−1)n
Conclusion:
The lateral displacement of the incident and emergent ray is given by:
D=tθ(n−1)n
- Consider a parallel slab of thickness t and refractive index n.
- A ray of light strikes the slab at an angle θ (the angle of incidence).
- When the ray enters the slab, it bends towards the normal due to the higher refractive index of the slab compared to air.
- Let R be the angle of refraction in the slab.
- According to Snell's Law:
n1sinθ=n2sinR
- Here, n1=1 (refractive index of air) and n2=n (refractive index of the slab).
- Thus, we have:
sinθ=nsinR
- For small angles, we can approximate sinθ≈θ and sinR≈R.
- From the equation sinθ=nsinR, we can express sinR:
sinR=sinθn≈θn
- The lateral displacement D can be calculated using the formula:
D=tcosR(sinθ−sinR)
- For small angles, cosR≈1 and sinR≈θn:
D≈t(θ−θn)
- Simplifying this gives:
D≈tθ(1−1n)
- Therefore, the lateral displacement D is:
D=tθ(n−1)n
The lateral displacement of the incident and emergent ray is given by:
D=tθ(n−1)n
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - B. More than one option is correct
20 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - C. comprehension type question
14 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
Similar Questions
A ray of light is incident on one face of a transparent slab of thickness 15 cm. The angle of incidence is 60∘. If the lateral displacement of the ray on emerging from the parallel plane is 5√3 cm, the refractive index of the material of the slab is
View SolutionA ray of light is incident on one face of a transparent glass slab of thickness 9cm at an angle of incidence 60∘. Lateral displacement of the ray on emerging from the opposite parallel face is 3√3cm. Refractive index of the material of slab is:
View SolutionA light ray is incident on a transparent slab of refractive index μ=√2 at an angle of incidence π/4. Find the ratio of the lateral displacement suffered by the light ray to the maximum value which it could have suffered.
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA ray of light is incident on a transparent glass slab of refractive index √3. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence?
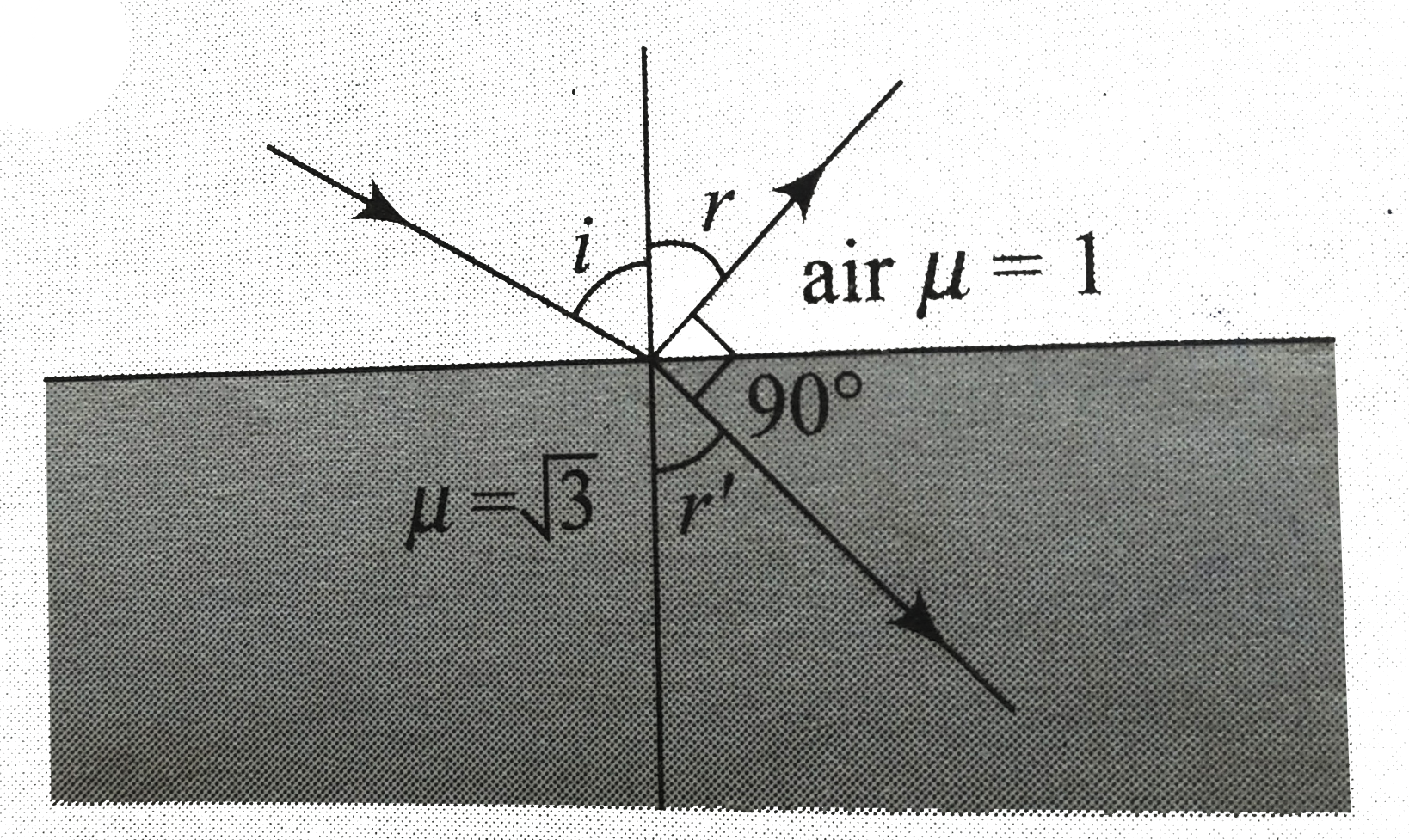
View SolutionLight ray is incident on a prism of angle A=60∘ are refractive index μ=√2. The angle of incidence which the emergent rays grazes the surface is given
View SolutionA ray of light is incident normally on a plane glass slab. What will be (i) the angle of refraction, and (ii) the angle of deviation for the ray ?
View SolutionA ray of light is incident on the surface of a glass plate of refractive index √3 at the polarising angle . The angle of incidence and angle of refraction of the ray is
View SolutionA ray of light is incident on a prism whose refractive index is 1.52 at an angle of 40∘. If the angle of emergence is 60∘, calculate the angle of the prism.
View SolutionUnpolarized light is incident on a plane glass surface having refractive index . The angle of incidence at which reflected and refracted rays would become perpendicular to each other is :
View Solution
