Linear mss density (mass/length) of a rod depends on the distanec from one end (say A) as λx=(αx+β) here α and β are constants, find the moment of inertia of this rod about an axis passing through A and perpendicular to the rod. Length of the rod is l.
I=∫I0dI=∫l0(dm)x2
=∫l0(λXdx)x2
=∫l0(αx+β)x2dx
=αl44+βl33
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2 Single Correct
Explore 26 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 2 Multiple Correct
Explore 36 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Level 1 Objective
Explore 30 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
A 1m long rod has a mass of 0.12 kg. The moment of inertia about an axis passin through the centre and perpendicular to the length of rod will be
View SolutionTwo identical rods each of mass M and length L are kept according to figure. Find the moment of inertia of rods about an axis passing through O and perpendicular to the plane of rods.
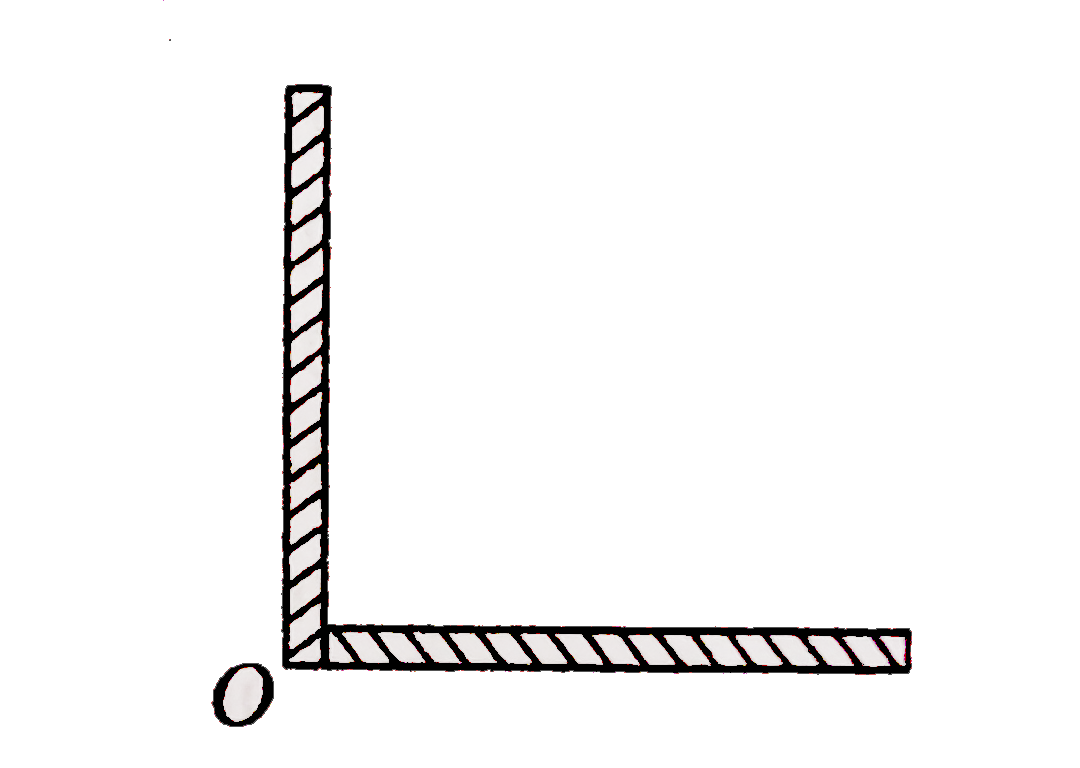
View Solution
Knowledge Check
A rod of length 2 m, has a mass of 0.12 kg. Its moment of inertia about an axis passing through its one end and perpendicular to the length of the rod is
A0.16 kg - m2B0.12 kg - m2C0.32 kg - m2D0.08 kg - m2A thin rod of length l and mass m is turned at mid-point O at angle of 60°. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
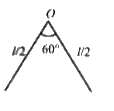 Aml2/3Bml26Cml28Dml212
Aml2/3Bml26Cml28Dml212A thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be
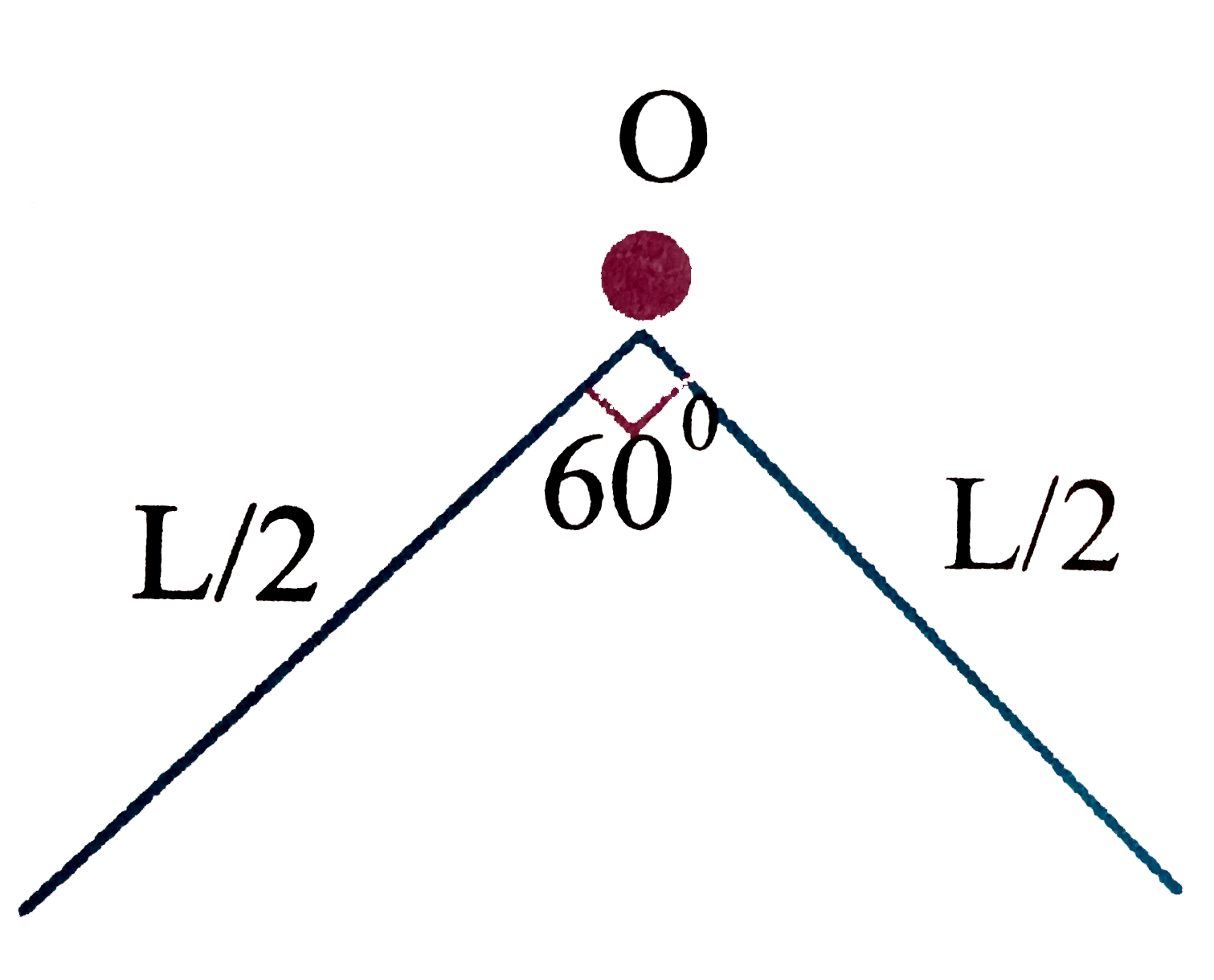 AML26BML212CML224DML23
AML26BML212CML224DML23

Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionThe moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is
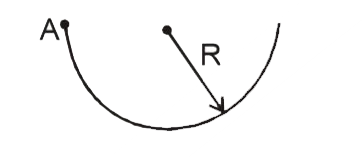
View SolutionThe moment of inertia of thin rod of linear density λ and length l about an axis passing through one end and perpendicular to its length is
View SolutionA thin rod of length L of mass M is bent at the middle point O at an angle of 60∘. The moment of inertia of the rod about an axis passing through O and perpendicular to the plane of the rod will be

View Solution