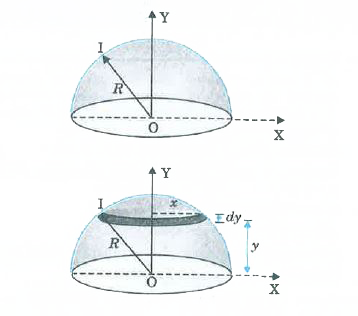
Locate the position of the centre of mass of a hemisphere of radius R as shown in the following figure:
Video Solution
Text Solution
Let the density of hemisphere be ρ. The hemisphere is constructed with a large number of co-axial discs. One such elementary disc of radius and thickness dy is at a distance y from the origin as shown above. Here the radius of the elemental disc is, x=√R2−y2
Mass of the elementary disc=Volume × density
=(πx2dy)=π(R2−y2)dyρ
The Y-coordinate of centre of mass are given by
Ycm=1m∫dmy
Here, m=23πR3ρ
Ycm=1m∫ydm=1m∫R0yπ(R2−y2)ρdy
=πρm∫R0(R2y−y3)dy
=πρm[R2y22−y44]R0
=πρm[R42−R44]=πρm(R44)
=πρ23πR3ρ(R44)=38R
Also, Zcm=∫zdm=0andXcm=∫xdm=0
∴ The coordinates of centre of mass are (0,38R,0)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - PRACTICE PROBLEMS26videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Conceptual Questions24videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
- BOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST15videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3 - Question 2 - Select One
Find distance of centre of mass of solid hemisphere of radius 8cm from centre
A3 cmB3/8 cmC4 cmD2 cm - Question 3 - Select One
What will be the position of centre of mass of a half disc shown ?
 .A2aπB4a3πCaπD2a3π
.A2aπB4a3πCaπD2a3π
Locate the position of centre of mass of a uniform plate of Mass m as shown in fig 4E 34
 View Solution
View SolutionThe centre of gravity of a solid hemisphere of radius a is
View SolutionThe centre of gravity of a solid hemisphere of radius a is : (A)
View SolutionFind out the position of centre of mass of the uniform lamina as shown in figure.
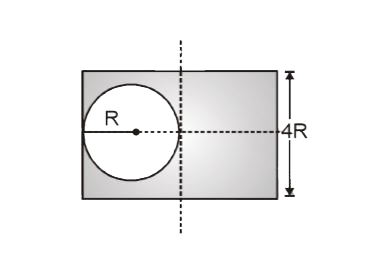 View Solution
View SolutionFind the position of centre of mass of the uniform lamina shown in figure.
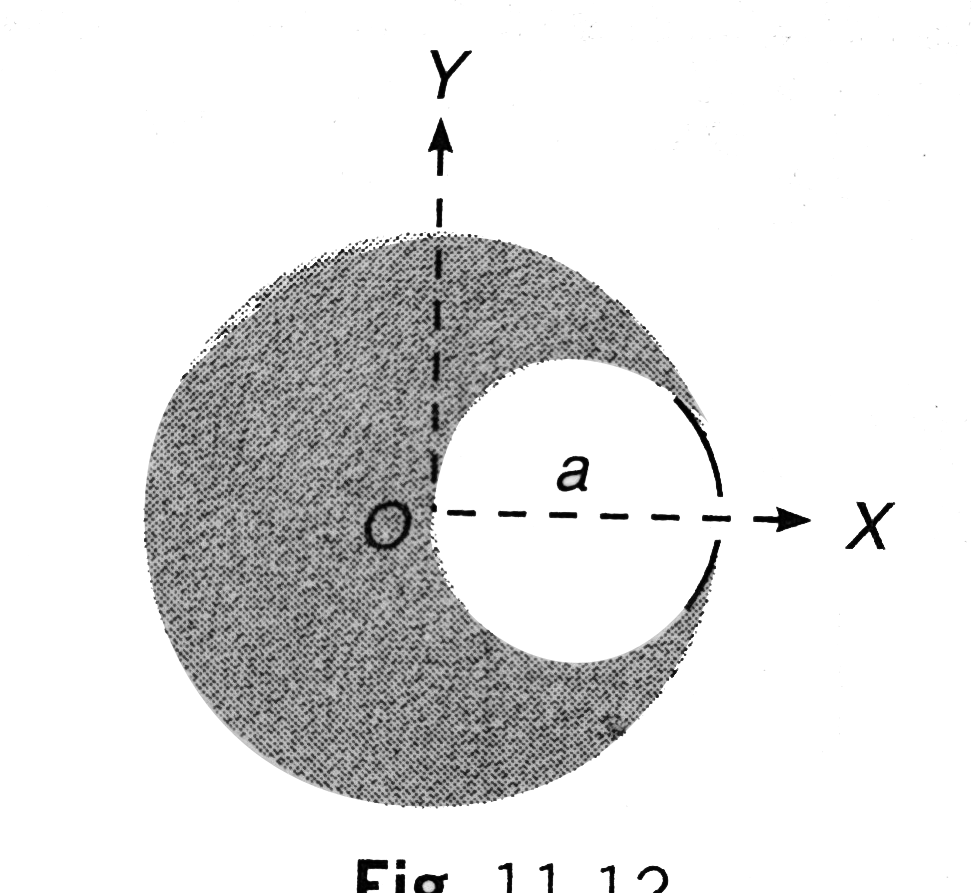 View Solution
View Solution

