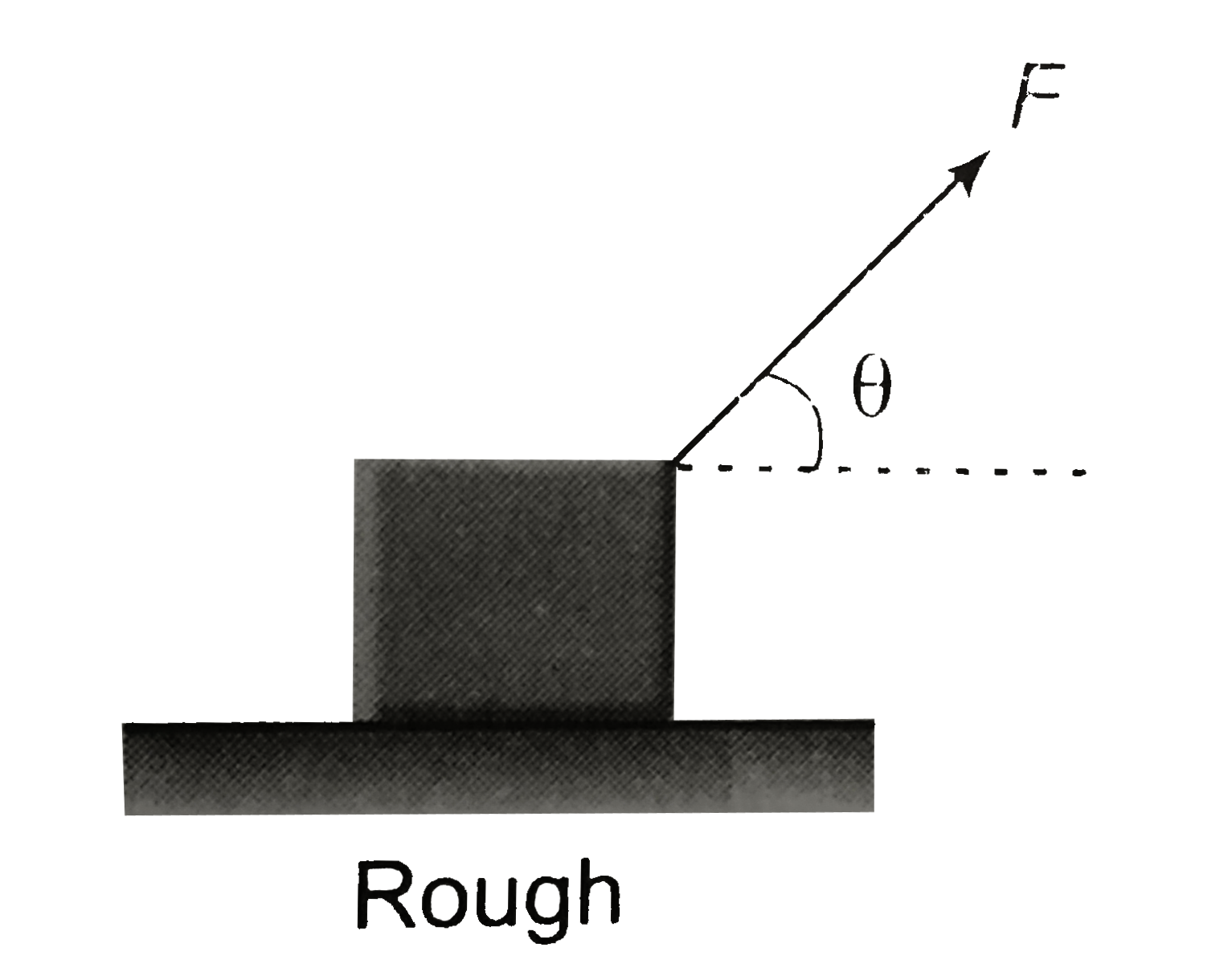
Minimum force is needed to move a block on rought surface, if θ= angle of friction.
Angle of friction and angle of repose are numerically same.
If both Accertion and Reason are true and the reason is correct explanation of the Assertion.
If both Assertion and Reason are true but reason is not the correct explanation of Assertion.
If Assertion is true, but the Reason is false.
If Assertion is false but the Reason is true.
The correct Answer is:B
N=mg−Fsinθ

Fcosθ=μN=μ(mg−Fsinθ)
∴F=μmgcosθ+μsinθ=f(θ) …(i)
For F to be minimum, denominator should be maximum.
or ddθ(cosθ+μsinθ)=0
From here we get θ=tan−1(μ)=angle of friction. with this value of θ we can also find that minimum value of force required from Eq. (i).
Similar Questions
Knowledge Check
The coefficent of friction μ and the angle of friction λ are related as
Asinλ=μBcosλ=μCtanλ=μDNone of these
Define angle of friction and angle of repose. Show that both are numerically equal.
View SolutionWhat is the relation between coefficient of friction and angle of repose ?
View SolutionStatic and Kinetic Friction|| Angle OF Friction|| Angle OF Repose
View SolutionStatic and Kinetic Friction || Angle OF Friction
View SolutionA force of 98N is just able to move a body of weight 45kg on a rough horizontal surface What are the coefficient of friction and angle of friction ? .
View SolutionA force of 98N is just able to move a body of weight 45kg on a rough horizontal surface What are the coefficient of friction and angle of friction ? .
View SolutionThe minimum force required just to move a block on a rough horizontal surface is 10 N An applied force of 5 N fails to move the block. What are the values of static friction and dynamic friction ?
View Solution
