n identical bulbs are connected in series and illuminated by a power supply . One of the bulbs gets fused. The fused bulb is removed , and the remaining bulbs are again illuminated by the same power supply. Find the fractional change in the illuminated of (a) all the bulbs and (b) one bulb.
To solve the problem step by step, we will analyze the situation before and after one bulb gets fused and is removed from the series circuit.
Step 1: Define the parameters
Let:
- n = number of identical bulbs
- V = voltage of the power supply
- R = resistance of each bulb
Step 2: Calculate the total resistance before the bulb fuses
When all n bulbs are connected in series, the total resistance Req is given by:
Req=nR
Step 3: Calculate the power consumed by all bulbs before one fuses
The power P1 consumed by the entire circuit when all bulbs are functioning is given by:
P1=V2Req=V2nR
Step 4: Calculate the power consumed by one bulb before the fuse
The power P2 consumed by each bulb when all are functioning is:
P2=P1n=V2n2R
Step 5: Calculate the total resistance after one bulb fuses
When one bulb fuses and is removed, the remaining number of bulbs is n−1. The new total resistance R′eq is:
R′eq=(n−1)R
Step 6: Calculate the power consumed by the remaining bulbs after one fuses
The new power P′1 consumed by the remaining bulbs is:
P′1=V2R′eq=V2(n−1)R
Step 7: Calculate the power consumed by one bulb after the fuse
The power P′2 consumed by each of the remaining bulbs is:
P′2=P′1n−1=V2(n−1)2R
Step 8: Calculate the fractional change in power for all bulbs
The fractional change in power for all bulbs is given by:
Fractional Change for all bulbs=P′1−P1P1=V2(n−1)R−V2nRV2nR
Simplifying this:
=n−(n−1)n−1=1n−1
Step 9: Calculate the fractional change in power for one bulb
The fractional change in power for one bulb is given by:
Fractional Change for one bulb=P′2−P2P2=V2(n−1)2R−V2n2RV2n2R
Simplifying this:
=n2−(n−1)2(n−1)2=n2−(n2−2n+1)(n−1)2=2n−1(n−1)2
Final Answers:
- (a) The fractional change in illumination of all the bulbs is 1n−1.
- (b) The fractional change in illumination of one bulb is 2n−1(n−1)2.
Let:
- n = number of identical bulbs
- V = voltage of the power supply
- R = resistance of each bulb
When all n bulbs are connected in series, the total resistance Req is given by:
Req=nR
The power P1 consumed by the entire circuit when all bulbs are functioning is given by:
P1=V2Req=V2nR
The power P2 consumed by each bulb when all are functioning is:
P2=P1n=V2n2R
When one bulb fuses and is removed, the remaining number of bulbs is n−1. The new total resistance R′eq is:
R′eq=(n−1)R
The new power P′1 consumed by the remaining bulbs is:
P′1=V2R′eq=V2(n−1)R
The power P′2 consumed by each of the remaining bulbs is:
P′2=P′1n−1=V2(n−1)2R
The fractional change in power for all bulbs is given by:
Fractional Change for all bulbs=P′1−P1P1=V2(n−1)R−V2nRV2nR
Simplifying this:
=n−(n−1)n−1=1n−1
The fractional change in power for one bulb is given by:
Fractional Change for one bulb=P′2−P2P2=V2(n−1)2R−V2n2RV2n2R
Simplifying this:
=n2−(n−1)2(n−1)2=n2−(n2−2n+1)(n−1)2=2n−1(n−1)2
- (a) The fractional change in illumination of all the bulbs is 1n−1.
- (b) The fractional change in illumination of one bulb is 2n−1(n−1)2.
Topper's Solved these Questions
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Subjective
8 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Single Correct
60 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Solved Examples
13 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Integer Type
4 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Concept Based
8 Videos
Similar Questions
3 identical bulbs are connected in series and these together dissipate a power P . If now the bulbs are connected in parallel, then the power dissipated will be
View SolutionSome electric bulbs are connected in series across a 220 V supply in a room. If one bulb is fused then remaining bulbs are connected again in series across the same supply. The illumination in the room will
View SolutionTen 60 W, 220 V bulbs are connected in series to 220 V supply . Power consumed in the circuit is
View Solution40 electric bulb are connected in series across a 220V supply. After one bulb is fused the remaining 39 are connected again in series across the same supply. The illumination will be
View SolutionWhen three identical bulbs are connected in series. The consumed power is 10W. If they are now connected in pa rallel then the consumed power will be:-
View Solution60W-220V and 100W-220V bulbs are connected in series to 220V mains. The power consumption is more in the bulb of :
View SolutionThree identical bulbs are connected in parallel across an ideal sources of emf E .The ammeter A and voltmeter V are ideal . If bulb B3 gets fused, then
_PHY_E05_094_Q01.png)
View SolutionTwo identical bulbs are conneted in parallel across an ideal source of emf E . The ammeter A voltmeter V are ideal . If bulb B2 gets fused , then
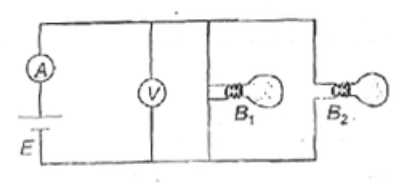 .
.
View SolutionTwo electic bulbs marked 25W−220V and 100W−220V are connected in series to a 440 V supply. Which of the bulbs will fuse?
View SolutionFigure shows three idenetical bulbs A,B and C connected to a battery of supply voltage V. When the switch S is closed, discuss the change is .
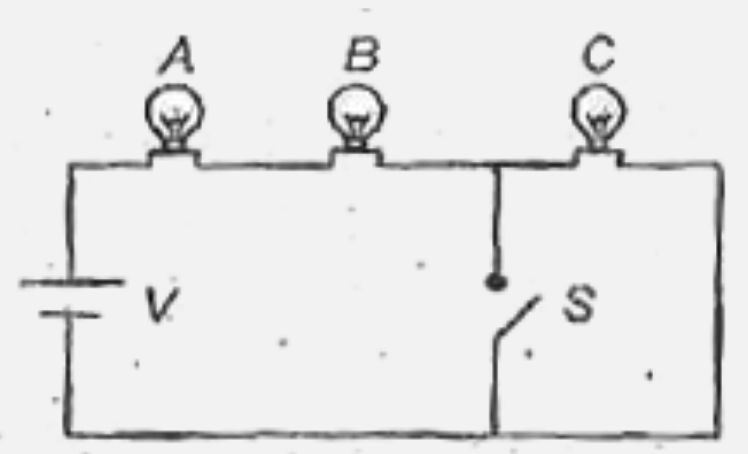
(a) The illumination of the three bulbs
(b) The power dissipated in the circuit .
View Solution
