n resistors each of resistance R first combine to give maximum effective resistgance and then combine to give minimum. The ratio of the maximum resistance is
n
n2
n2−1
n3
The correct Answer is:B
To get maximum equivalent resistance all resistances must be connected in series
∴(Req)max=R+R+R...ntimes=nR
To get minimum equivalent resistance all resistances myst be connected in parallel.
∴1(Req)min=1R+1R+....ntime,1(Req)min=nR
(Req)min=Rn∴(Req)max(Req)min=nRR/n=n2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Cells, Emf, Internal Resistance
6 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Cell In Series And In Parallel
3 Videos
- CURRENT ELECTRICITYBOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Electrical Energy, Power
7 Videos
- COMMUNITCATION SYSTEMSBOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Given n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View SolutionGiven n resistors each of resistane R, how will you combine them to get the (i) maximum, (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View Solution
Knowledge Check
n resistors, each of resistances R are first connected in series so as to give an effective resistance Rs Subsequently these resistors are connected in parallel so as to give an effective resistance Rp. Then the ratio RsRp will be
An:1Bn2:1C1:n2D1:nWe have n resistors each of resistance R. The ratio of the combination for maximum and minimum values is
AnBn2Cn3D1n
(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
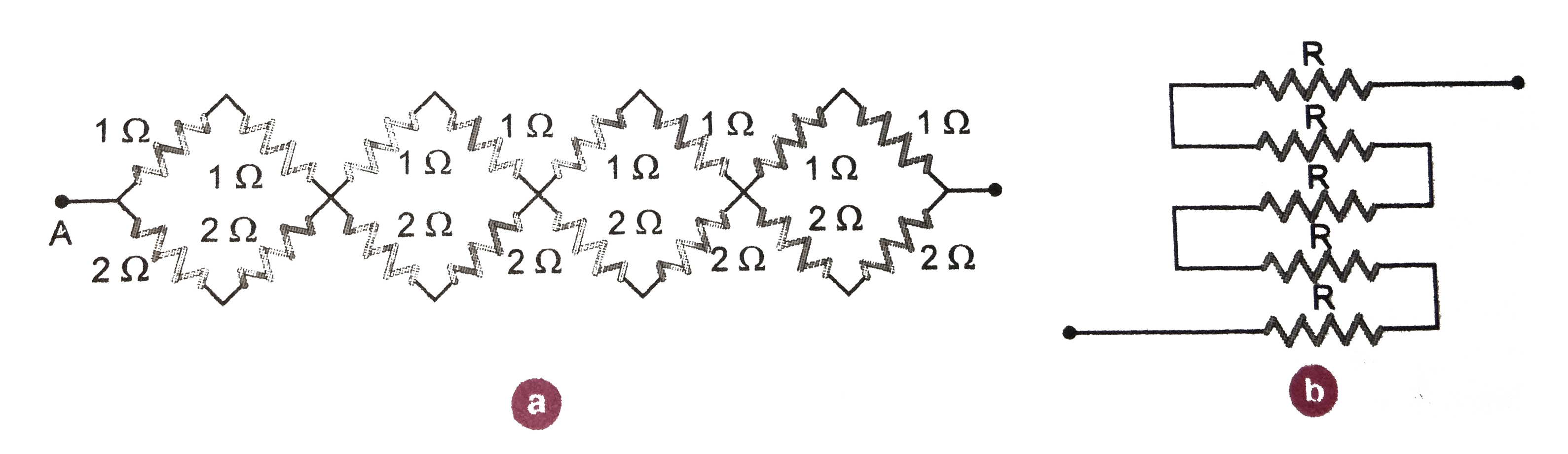
View SolutionGiven n resistors each of resistance R, how will you combine them to get the (i) maximum, and (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
View SolutionYou are given n resistors each of resistance r .These are first connected to get minimum resistance .In the secoind case these are again connected differently to get maximum possible resistance. Compute the ratio between the minimum and maximum value of resistance so obtained.
View SolutionIf n resistors each of resistance r are connected to get (i) maximum possible resistance (ii) minimum possible resistance. Compute the ratio between values of resistances obtained in (i) and (ii).
View SolutionThirteen resistors each of resistance R are connected in the circuit as shown . The effective resistance between A and B is
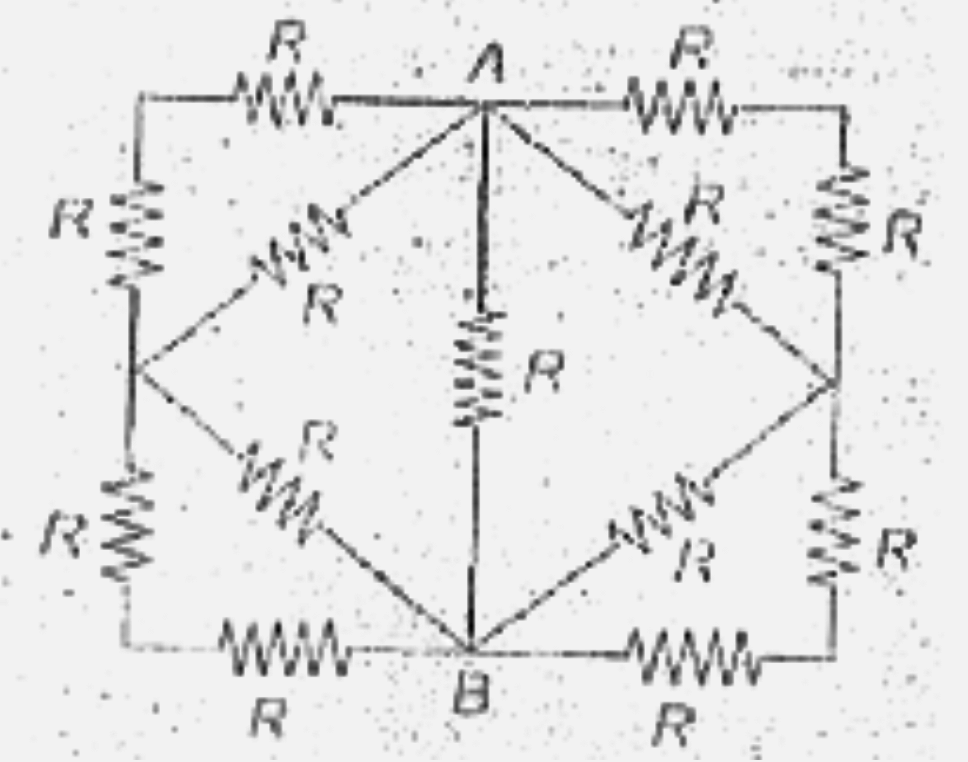
View SolutionYou are given 10 resistors each of resistance 2Ω. First they are connected to obtain possible minimum resistance. Then they are connected to obtain possible maximum resistance. The ratio of maximum and minimum resistance is ________________ .
View Solution
