Natural monochromatic light falls on a system of two crossed Nicol prisms between to its optical axis is insered. Find the minimum thickness of the plate at which this system will transmit η=0.30 of luuminous flux if the specific rotation constant of quartz is equal to α=17angdeg/mm.
If I0= intensity of natural light then
12I0= intensity of light emerging from the polarizer nicol.
Suppose the quartz plate rotates this light by φ, then the analyser will transmit
12I0cos2(90−φ)
=12I0sin2φ
of this intensity. Hence ηI0=12I0sin2φ
or φ=sin−1√2η
But φ=αd so
dmin=1αsin−1√2η
for minimum d we must take the principle value of inverse sine. Thus using α=17angdeg/nm.
dmin=2.99mm

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Optics Of Moving Sources
22 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Light passes through a system of two crossed Nicol prisms between which a quartz plate cut at right angles to its optical axis is placed. Determine the minimum thickness of the plate which allows light of wavelength 436nm to be complately cut off by the system and transmits half the light of wavelength 497nm. The specific rotation constant of quartz for these wavelength is equal to 41.5 and 31.1 angualr degress per mm respectively.
View SolutionA beam of natural light of intensity I0 falls on a system of two crossed Nicol prisms between which a tube filled with certain solution is placed in a longitudinal magnetic field of strength H. The length of the tube is l, the coefficient of linear absorption of solution is x, and the verder constant is V. Find the intensity of light transmitted through that system.
View SolutionWhite natural light falls on a system of two crossed Nicol prisms having between them a quartz plate 1.50mm thick, cut parallel to the optical axis. The axis of the plate froms an angle of 45∘ with the principle directions of the Nicol prism. The light transmitted through that system was split into the spectrum. How many dark fringes will be observed in the wavelength interval from 0.55 to 0.66μm? The difference of refractve indices for ordinary and extraordianry rays in that wavelength interval is assumed to be equal to 0.0090.
View SolutionNatural monochromatic light of intensity I0 falls on a system of two Polaroids between which a crystalline plate is inserted,cut parallel to its optical axis. The plate introduces a phase difference δ between the ordinary and extraodianry rays. demonstrate that the intensity of light transmitted through that sysytem is equal to
I=12I0[cos2(φ−φ')−sin2φ.sin2φ'sin2(δ/2)],
where φ and φ' are the angles between the optical axis of the crystal and the principle directions of the Polaroids. In particular, consider the cases of crossed and parallel Polaroids.
View SolutionA quartz plate cur parallel to the optical axis placed between two crossed Nicol prisms. The angle between the principal directions of the Nicol prism and the plate is equal to 45∘. The thckness of the plate is d=0.50mm. At what wavelengths in the interval from 0.50 to 0.60μm is the intensity of light which passed through that system independent of rotation of the rear prism? The difference of refractive indices for ordinary and extraordinary rays in that wavelength interval is assumed to be Δn=0.0090.
View SolutionA quartz plate cut parallel to its optical axis is placed between two corssed Nicol prisms so that principle directions form an angle of 45∘ with the optical axis of the plate. What is the minimum thickness of that plate transmitting light of wavelength λ=643nm with maximum intensity while greatly reducing the intensity of transmitting light of wavelength λ2=564nm? The difference of refractive indieces indices for extroardianry and ordinary rays is assumed to be equal to ne−n0=0.0090 for both wavelengths.
View SolutionPlane-polarized light of wavelength 0.59μm falls on a trihedral quartz prism P (Fig.) with refracting angle Θ=30∘. Inside the prism light propagates along the optical axis whose direction is shwon by hatching. Behind the Polaroid Pol an interference pattern of bright and dark fringes of width Δx=15.0mm is pbserved. Find the specific rotation constant of quartz and the distribution of intensity of light behind the Polaroid.
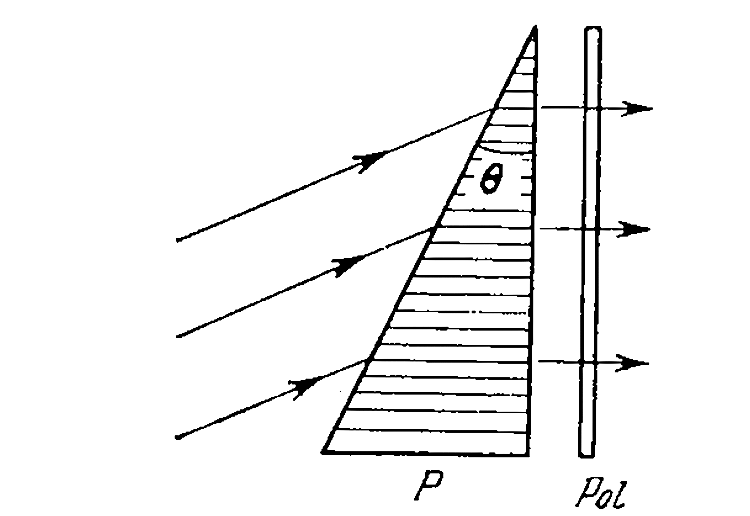
View SolutionOne has to manufacture a quartz plate cur parallel to its optical axis and not exceeding 0.50mm is thickness. Find the maximum thickness of the plate allowing plane-polarized light with wavelength λ=589nm
(a) to experience only rotation of polarization plane,
(b) to acquire circular polarization after passing through that plane.
View SolutionLight with wavelength λ falls on a system of crossed polarizer P and analyzer A between which a Babinet compesator C is inserted (Fig.). The compensator consists of two q2uartz wedges with the optical axis of one of them being parallel to the edge, and of the other, perpendicular to it. The principal directions of the polarizer and the analyser from an angle of 45∘ with the optical axes of the compensator. The refracting angle of the wedges is equal to Θ(Θ<<1) qand the difference of refractive indices of quartz is ne−n0. The insertion of investigated birefringent sample S, with the optical axis oriented as shown in the figure, results in displacement of the fringe upward by δxmm. Find:
the width of the fringe Δx,
(b) the magnitude and the sign of the optical path difference of ordinary and extraordianry rays, which appears due to the sample S.

View SolutionMonochromatic light with circular polarization falls normally on a crystalline plate cut parallel to the optical axis. Behind the plate there is a Nicol prism whose principle direction froms an angle φ with the optical axis of the plate. Demonsrate that the intensity of light transmitted through that system is equal to
I=I0(1+sin2φ.sinδ),
where δ is the phase difference between the ordianry and extraordinary rays which is introduced by the plate.
View Solution
