Obtain a relation for the distance travelled by an object moving with a unifrom acceleration in the interval between 4th and 5th seconds.
To find the relation for the distance travelled by an object moving with uniform acceleration between the 4th and 5th seconds, we can use the equations of motion.
1. Understand the Problem:
We need to find the distance travelled by an object in the interval between the 4th second and the 5th second.
2. Use the Equation of Motion:
The equation for distance travelled under uniform acceleration is given by:
s=ut+12at2
where s is the distance, u is the initial velocity, a is the acceleration, and t is the time.
3. Calculate Distance at t=5 seconds:
Substitute t=5 into the equation:
s5=u(5)+12a(52)
Simplifying this gives:
s5=5u+12a(25)=5u+252a
4. Calculate Distance at t=4 seconds:
Now substitute t=4 into the equation:
s4=u(4)+12a(42)
Simplifying this gives:
s4=4u+12a(16)=4u+8a
5. Find the Distance Travelled Between 4th and 5th Seconds:
The distance travelled between the 4th and 5th seconds is given by:
s4 to 5=s5−s4
Substituting the expressions we found:
s4 to 5=(5u+252a)−(4u+8a)
6. Simplify the Expression:
s4 to 5=5u+252a−4u−8a
Combine like terms:
s4 to 5=(5u−4u)+(252a−8a)
s4 to 5=u+(252a−162a)
s4 to 5=u+92a
Final Relation:
Thus, the distance travelled by the object between the 4th and 5th seconds is:
s4 to 5=u+92a
---
We need to find the distance travelled by an object in the interval between the 4th second and the 5th second.
The equation for distance travelled under uniform acceleration is given by:
s=ut+12at2
where s is the distance, u is the initial velocity, a is the acceleration, and t is the time.
Substitute t=5 into the equation:
s5=u(5)+12a(52)
Simplifying this gives:
s5=5u+12a(25)=5u+252a
Now substitute t=4 into the equation:
s4=u(4)+12a(42)
Simplifying this gives:
s4=4u+12a(16)=4u+8a
The distance travelled between the 4th and 5th seconds is given by:
s4 to 5=s5−s4
Substituting the expressions we found:
s4 to 5=(5u+252a)−(4u+8a)
s4 to 5=5u+252a−4u−8a
Combine like terms:
s4 to 5=(5u−4u)+(252a−8a)
s4 to 5=u+(252a−162a)
s4 to 5=u+92a
Thus, the distance travelled by the object between the 4th and 5th seconds is:
s4 to 5=u+92a
Topper's Solved these Questions
- MOTIONBOOK - PRADEEPCHAPTER - MOTIONEXERCISE - very short answer queation
25 Videos
- MOTIONBOOK - PRADEEPCHAPTER - MOTIONEXERCISE - Short answer questions
15 Videos
- MOTIONBOOK - PRADEEPCHAPTER - MOTIONEXERCISE - NCERT short answer question
7 Videos
- GRAVITATIONBOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Model Test paper (1)
36 Videos
- SOUNDBOOK - PRADEEPCHAPTER - SOUNDEXERCISE - Model Test (sec - B)
12 Videos
Similar Questions
The distance travelled by a particle starting from rest and moving with an acceleration 4/3m/s2 ,in the third-second is
View SolutionShow that area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in the interval.
View Solution
Knowledge Check
The distance travelled by a particle starting from rest and moving with an acceleration 43ms−2, in the third second is.
A6 mB4 mC103mD193mA body starting from rest is moving with a uniform acceleration of 8ms2. Then the distance travelled by it in 5th second will be
A40mB36mC100mDzeroA particle starts moving with acceleration 2m/s2. Distance travelled by it in 5th half second is
A1.25 mB2.25 mC6.25 mD30.25 m
Show that the area under the velocity-time graph of an object moving with constant acceleration in a straight line in certain time interval is equal to the distance covered by the object in that interval.
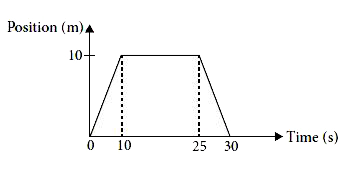
View SolutionThe given figure shows the position-time graph of an object. Find the ratio of the velocities at 5th and 27th second
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f. If the sum of the distances travelled in tthand(t+1)th seconds is 100cm, then its velocity after t seconds, in cm/s, is.
View SolutionA body starting from rest and has uniform acceleration
8m/s2 . The distance travelled by it in5th second will be
View SolutionA body starting from rest and has uniform acceleration
8m/s2 . The distance travelled by it in5th second will be
View Solution
