Obtain the maximum kinetic energy of β-particles, and the radiation frequencies of γ decays in the decay scheme shown in Fig. 14.6. You are given that m(.198Au)=197.968233u,m(.198Hg)=197.966760u
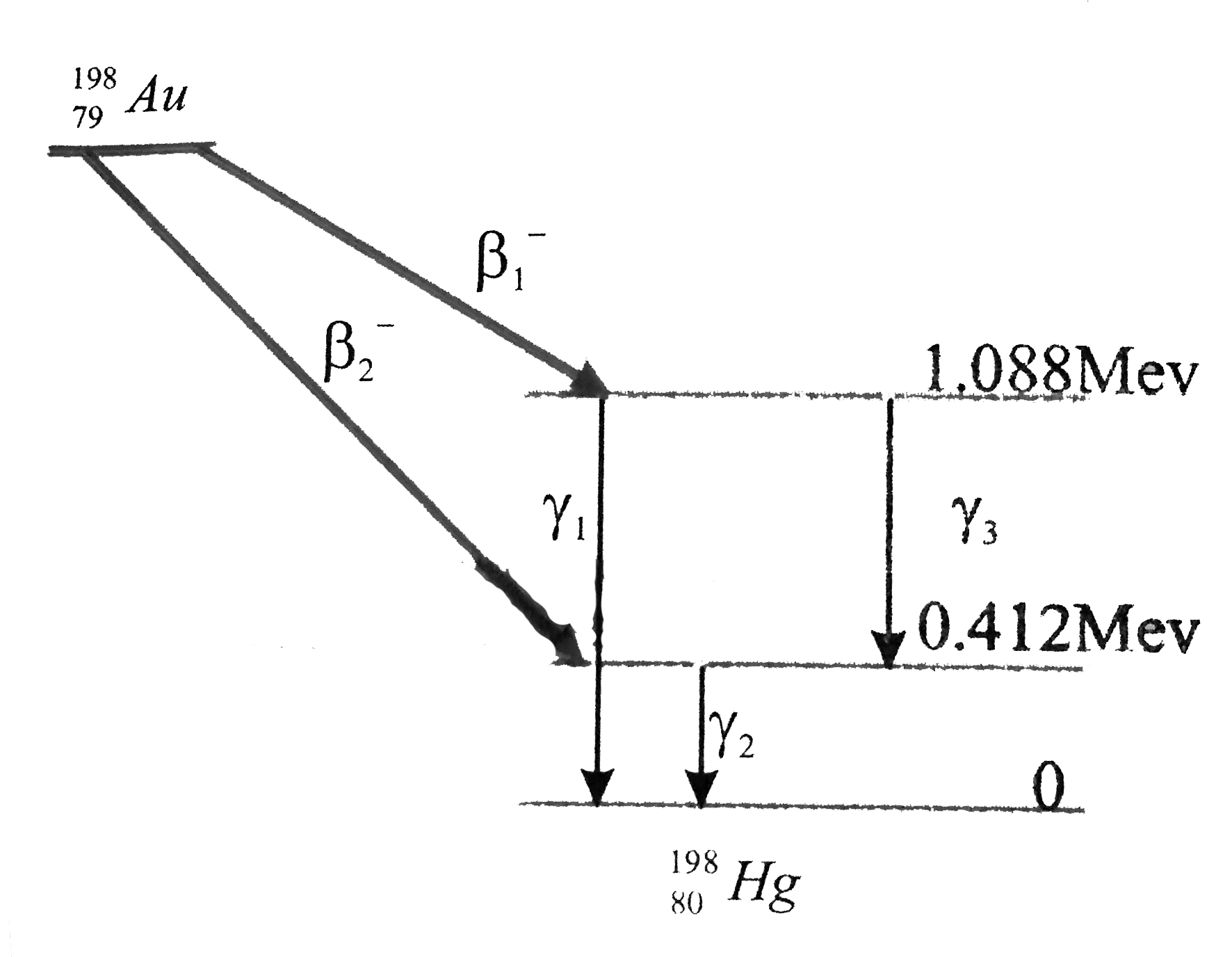
It can be observed from the given Y-decy diagram that y1 decays from the 1.088 MeV energy level to the 0 MeV energy level.
Hence, the energy corresponding to y1-decay is given as :
E1=1.088-0=1.088 MeV
hv1=1.088×1.6×10−19×106J
Where, h=Planck's constant =6.6×10−34Js
v1= Frequency of radiation radiated by y1-decay
∴v1=E1h
=1.088×1.6×10−19×1066.6×10−34=2.637×1020Hz
It can be observed form the given y-decay diagram that y2 decays from the 0.412 MeV energy level to the 0MeV energy level.
Hence, the energy corresponding to y2-decay is given as:
E2=0.412−0=0.412MeV
hv2=0.412×1.6×10−19×106J
Where,
v2= Frequency of radation radiated by y2- decay
∴v2=E2h
=0.412×1.6×140−19×1066.6×10−34=9.988×1019Hz
It can be observed form the given y-decay diagram that y3 decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to y3-decay is given as :
E3=1.088−0.412=0.676MeV
hv3=0.676×10−19×106J
Where,
v3=Fequency of radiation radiated by y3-decay
∴v3=E3h
=0.676×1.6×10−19×1066.6×10−34=1.639×1020Hz
Mass of m(19878Au)=197.968233u
Mass of m(19880Hg)=197.966760ub
1u=931.5MeV/c2
Energy of the highest level is given as :
E=[m(19878Au)−m(19080Hg)]
=197.968233−197.966760=0.001473u
=0.001473×931.5=1.372099MeV
β1 decays from the 1.3720995 MeV level to the 1.088 MeV level
∴ Maximum kinetic energy of the β1 particle =1.3720995-1.088 =0.2840995 MeV
β2 decays from the 1.3720995 MeV level to the 0.412 MeV level
∴ Maximum kinetic energy of the β2 particle=1.3720995-0.412=0.9600995 MeV
Topper's Solved these Questions
Similar Questions
Calculate the kinetic energy of β-particles and the radiation frequencies corresponding to the γ-decays shown in figure.
Given, mass of .12Mg27 atom =26.991425 amu and mass of .13Al27 atom = 26.990080 amu

View SolutionCalculate the maximum kinetic energy of the bera particle emitted in the following decay scheme:
^12N rarr 12C∗+e++v
^12C rarr ^12C+γ(4.43MeV).
The atomic mass of 12Nis12.018612u.
View Solution
Knowledge Check
Gold .19879Au undergoes β− decay to an excited state of .19880Hg. If the excited state decays by emission of a γ-photon with energy 0.412MeV, the maximum kinetic energy of the electron emitted in the decay is (This maximum occurs when the antineutrino has negligible energy. The recoil energy of the .19880Hg nucleus can be ignored. The masses of the neutral atoms in their ground states are 197.968255u for .19879Hg).
A0.412MeVB1.371MeVC0.959MeVD1.473MeVGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
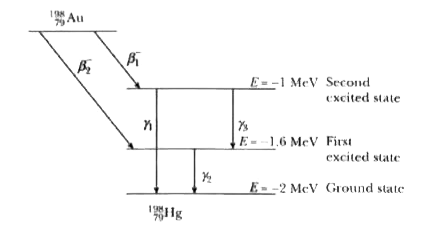
Whatis the maximum kinetic energy of emitted β2 particle?A1.44 MeVB0.59 MeVC1.86 MeVD1.46 MeVGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
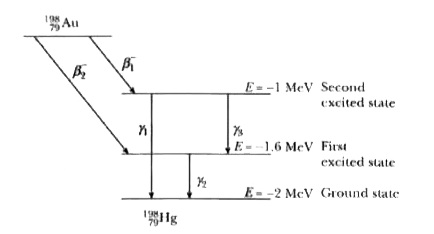
What is the maximum kinetic energy of emitted β1 parricle ?A1.28 MeVB0.77 MeVC1.86 MeVD0.86 MeV
Calculate the maximum energy that a β particle can have in the following decay:
.8O19→.9F19+.−1e0+¯¯¯V
Given, m(.8O19)=19.003576u,m(.9F19)=18.998403u,m(.−1e0)=0.000549u
View SolutionA nucleus 10Ne23 undergoes β- decay and becomes 11Na23 . Calculate the maximum kinetic energy of electrons emitted assuming that the daughter nucleus and antineutrino carry negligible kinetic energy. Given mass of 10Ne23 = 22.994466 u and mass of 11Na23 = 22.989770 m
View SolutionConsider one of the fission reactions of U235 by thernmal neutrons :
.92U235+n→.38Sr94+.54Ce140+2n
The fission fragments are, however, not stable. They unaergo successive β−decays unit .38Sr94 becomes .40Zr94 and .54Xe140 becomes .58Ce140. Estimate the total energy released in the process. Is all that energy available as kinetic energy of the fission products (Zr and Ce)? You are given that
m(U235)=255.0439amu, mn=1.00866amu m(Zr94)=93.9065amu, m(Ce140)=139.9055amu
View SolutionConsider the beta decay
^198Au→198Hg∗+Bη−1+→v.
where ^198Hg∗ represents a mercury nucleus in an excited state at energy 1.088MeV above the ground state. What can be the maximum kinetic energy of the electron emitted? The atomic mass of ^198Au is 197.968233u and that of ^198Hg is 197.966760u.
View SolutionGold nucleus (19879Au) can decay into mercuyr nucleus (19880Hg8) by two decay schemes shown in figure below (i) it can emit a β -particle (β1) and come to ground state by either emiting one γ- ray (γ1) or emitting two γ- rays (γ3 and γ4) (ii) It can emit one β- particle (β2) and come to ground state by emitting γ2 ray. Atomic masses: 198Au=197.9652 amu and 198Hg=197.9662 amu. Given that 1 amu= 930MeV/c2. The energy levels of the nucleus are shown in figure below
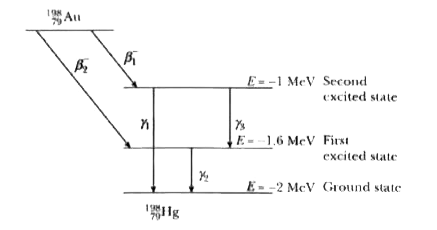
The wavelength of emitted γ - rays is the order
View Solution
