On a frictionless horizontal surface , assumed to be the x−y plane , a small trolley A is moving along a straight line parallel to the y−aξs( see figure) with a constant velocity of (√3−1)m/s . At a particular instant , when the line OA makes an angle of 45(∘) with the x−aξs , a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x−aξsandithitsthetrol≤y.<br>(a)Themotionoftheballisobservedomtheameofthetrol≤y.Calca––tethe∠thetamadebythevelocity→−−→roftheballwiththe x-axis in this frame .
(b) Find the speed of the ball with respect to the surface , if ϕ=(4θ)/(4).
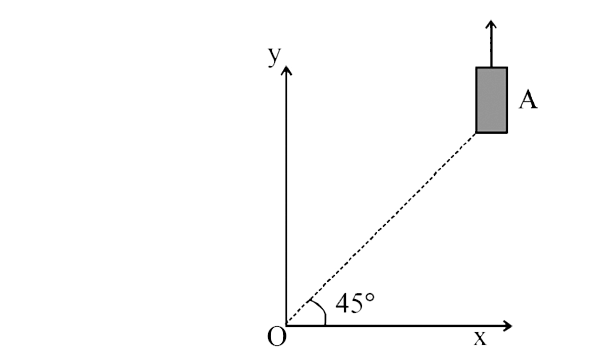
Method 1 : (a) Since the ball hits the trolley, relative to trolley, the velocity of ball should be directed towards the trolley. Hence, in the frame of trolley, the ball will appear to be moving towards OA, or in the frame of trolley, ball's velocity will make an angle of 45∘.
(b) ϕ=4θ3=4×45∘3=60∘
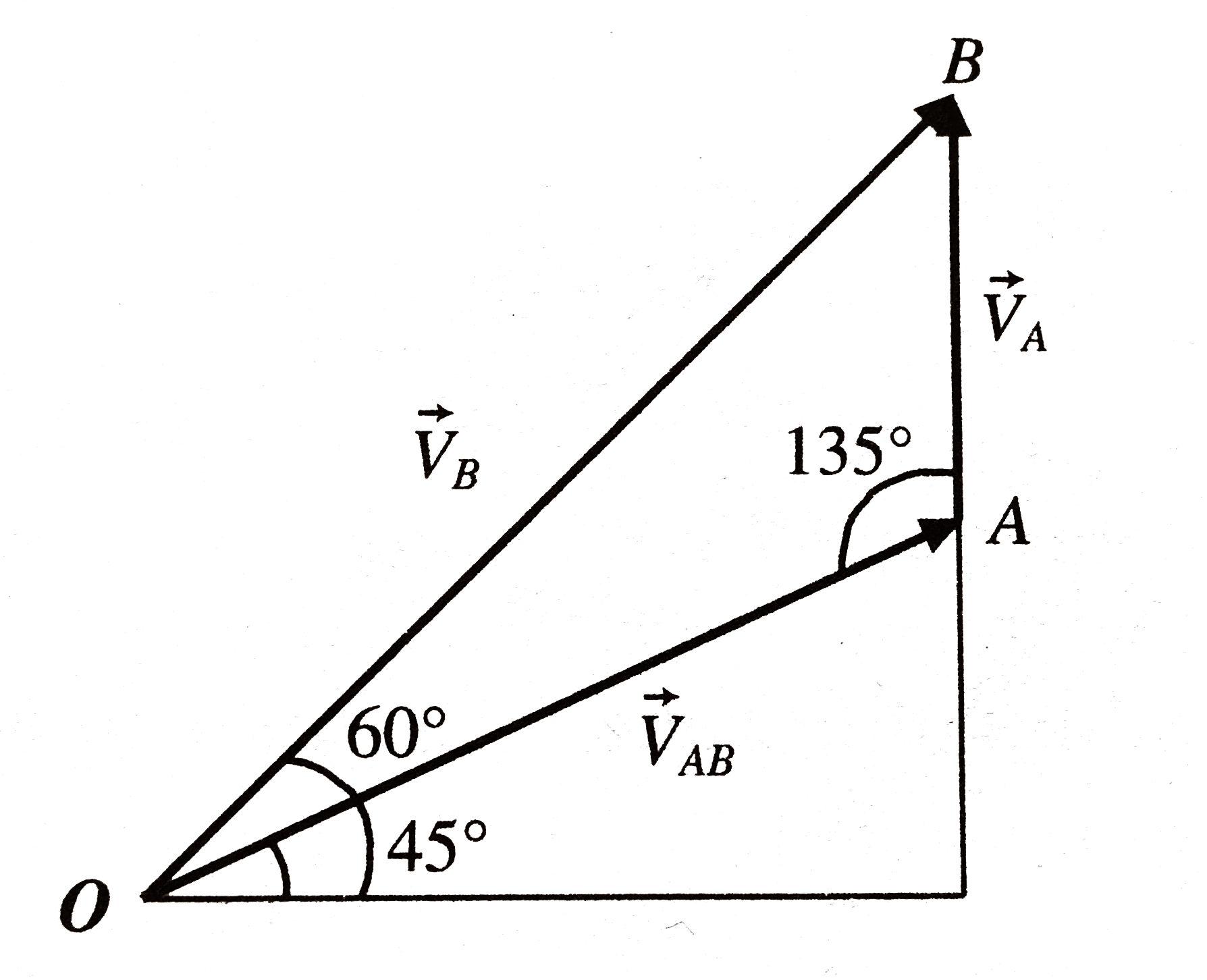
Using sine rule VBsin135∘=VAsin15∘
⇒VB=2ms−1
Method 2 : (a) Let A stands for trolley and B for ball.
Relative velocity of B will respect to A(→vBA) should be along OA for the ball to hit the trolley.
Hence, →vBA will make an angle of 45∘ with positive x - axis.
(b) tanθ=vBAyvBAx=tan45∘orvBAy=vBAx...(i)
Further vBAy=vBy−vAyorvBAx=vBx−0 ...(ii)
vBy−(√3−1)
tanθ=vByvBxorvBy=vBxtanϕ
From (i),(ii),(iii), and (iv), we get
vBx=(√3−1)tanϕ−1andvBy=(√3−1)tanθ−1tanϕ
ϕ=4θ3=43(45∘)
Speed of ball w.r.t. surface,
vB=√v2Bx+v2By=√3−1tanϕ−1secϕ
Substituting ϕ=60∘, we get vB=2ms−1.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.2
25 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise Integer
9 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
Knowledge Check
A particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
Adecreases with timeBincreases with timeCremains constantDis zeroA straight line makes an angle of 135∘ with the X-axis and cuts Y-axis at a distance -5 from the origin. The equation of the line is
A2x+y+5=0Bx+2y+3=0Cx+y+5=0Dx+y+3=0A straight line which makes an angle of 60∘ with each of Y and Z-axis, the angle this lines makes with X-axis is
A30∘B60∘C75∘D45∘
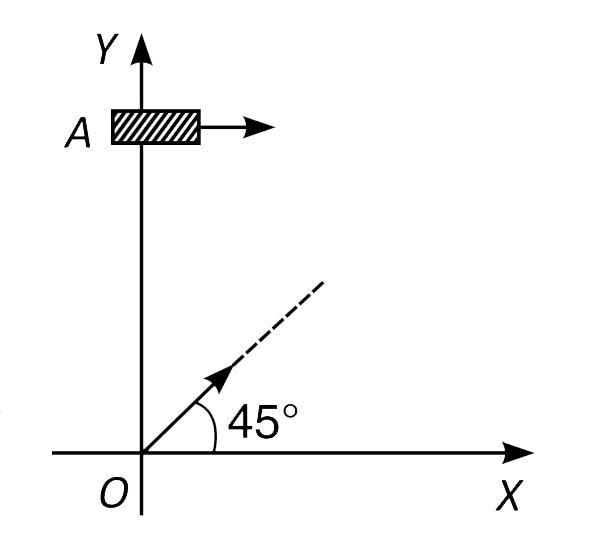
A small cart A starts moving on a horizontal surface, assumed to be x-y plane along a straight line parallel to x-axis (see figure) with a constant acceleration of 4m/s2. Initially it is located on the positive y-axis at a distance 9 m from origin. At the instant the cart starts moving, a ball is rolled along the surface from the origin in a direction making an angle 45° with the x-axis. The ball moves without friction at a constant velocity and hits the cart.
(a) Describe the path of the ball in a reference frame attached to the cart.
(b) Find the speed of the ball.
View SolutionEquations of Lines Parallel to the X-axis and Y-axis
View SolutionThe equation of a straight line which makes an angle 45° with the x-axis with y-intercept 101 units is
View SolutionThe equation of a straight line which makes an angle 45∘ with the x-axis with y-intercept 101 units is :
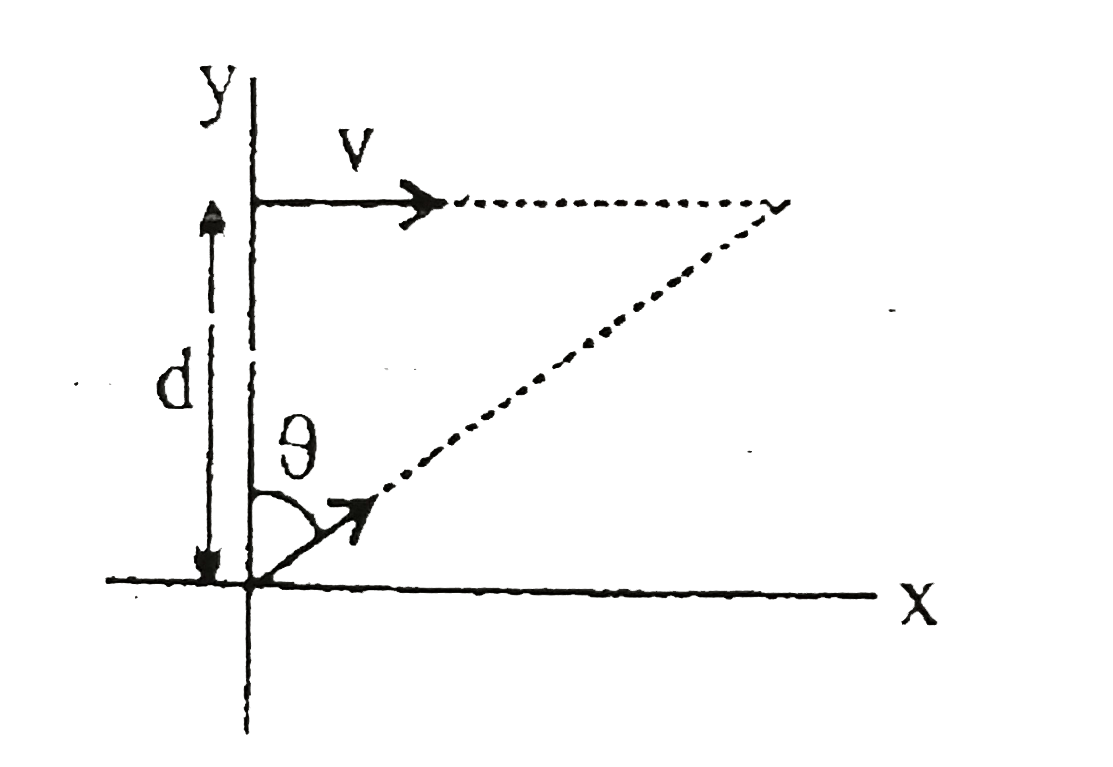
View SolutionA particle moves along a straight line parallel to x-axis at a distancce d=3m from it, with constant speed of v=3m/s. Another particle stats from the origin with constant acceleration a=4m/s2 at an angle θ with y-axis along a straight line at the instant the first particle crosses y-axis. Find 'theta' such that the two particle collide.
View Solution

