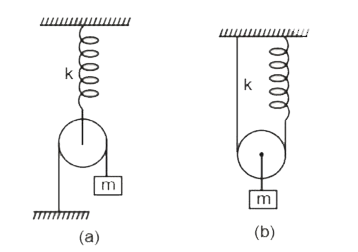
On applying a force F, point P is displaced vertically down by y from equilibrium positionl. Find force F in terms of the force constant k of the spring and displacement y, for the cases (a) and (b), as shown in fig.

case (a) At point P:F=T

And for the equilibrium of pulley
2T=Fs …(ii)
But as due to the shift of point P by y, the spring stretches by (y/2). So,
Fs=k(y/2) …(iii)
So substituting Fs from (iii) in (ii) and then T from (ii) in (i) we get
F=(k/4)y ..(A)
Case (b) As the tension in massless string and spring will be same,
T=F's ...(i)
For pulley: F=2F's...(ii)
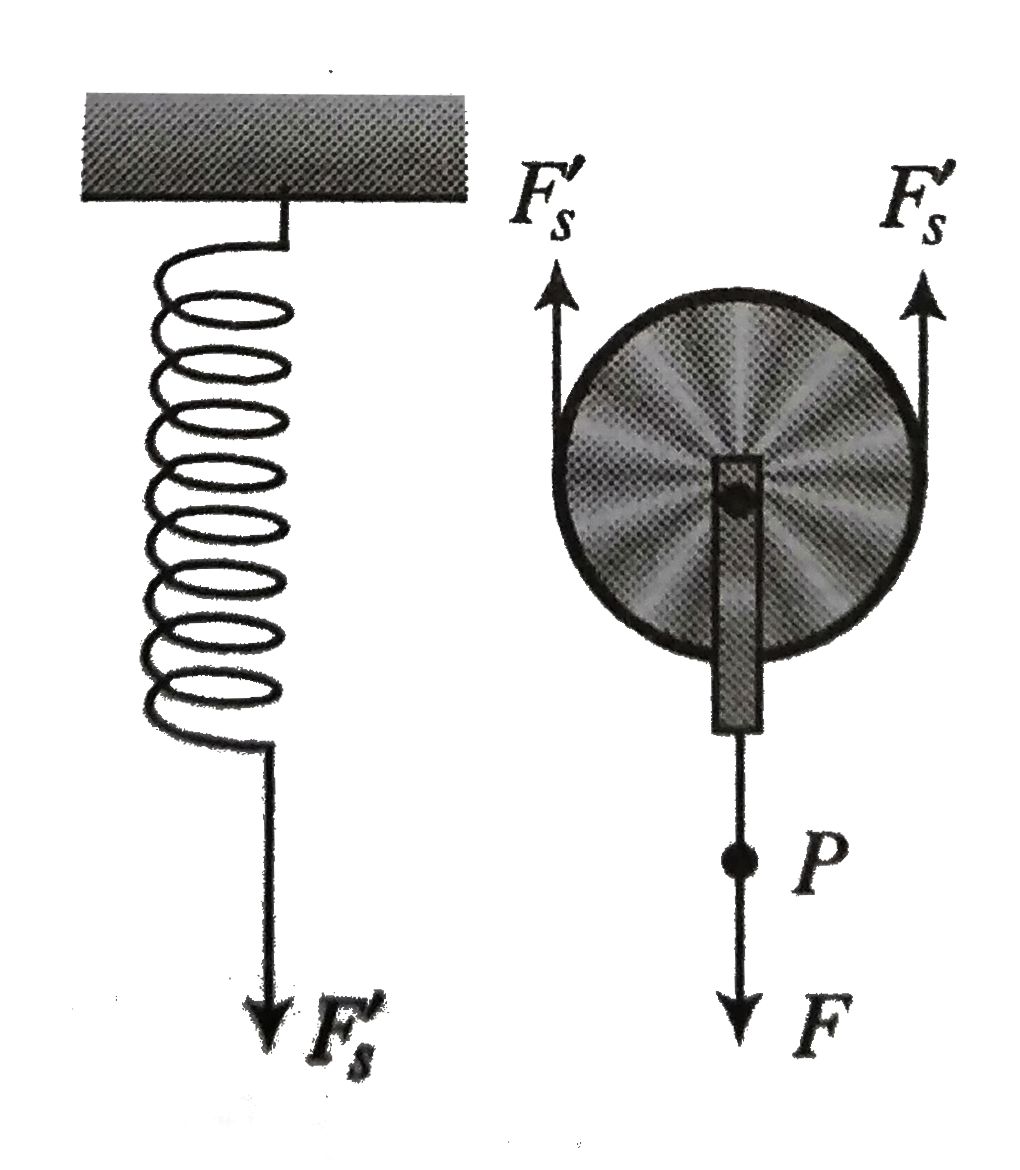
Now if the mass M shifts by y, the spring will stretch by 2y (as string is inextensible)
F's=k(2y) ...(iii)
So substituting F' from eq, (ii) in (iii)
F=(4k)y ..(B)
Force of spring does not change instantaneously.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Solved Examples
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Exercise 6.1
11 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
On applying a force F the mass M is displaced vertically down by from equilibrium position, Find the force F in terms of the force constant k of the spring and displacement y for the cases (A) and (B) as shown in
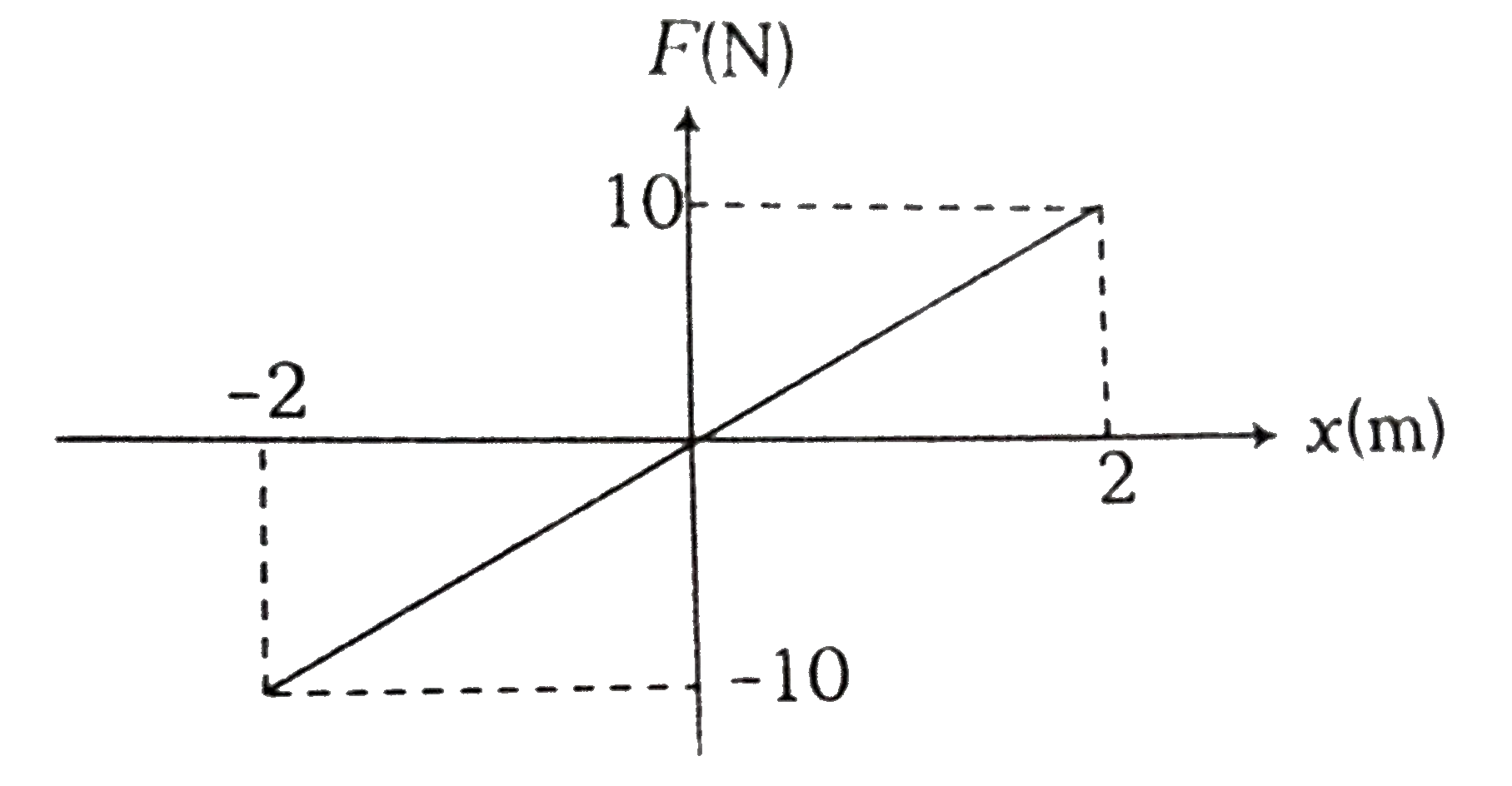
View SolutionThe force constant between the restoring force F and displacement x of a spring accoring to the graph shown will be
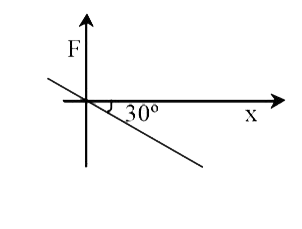
View Solution
Knowledge Check
The value of force constant between the applied elastic force F and displacement will be
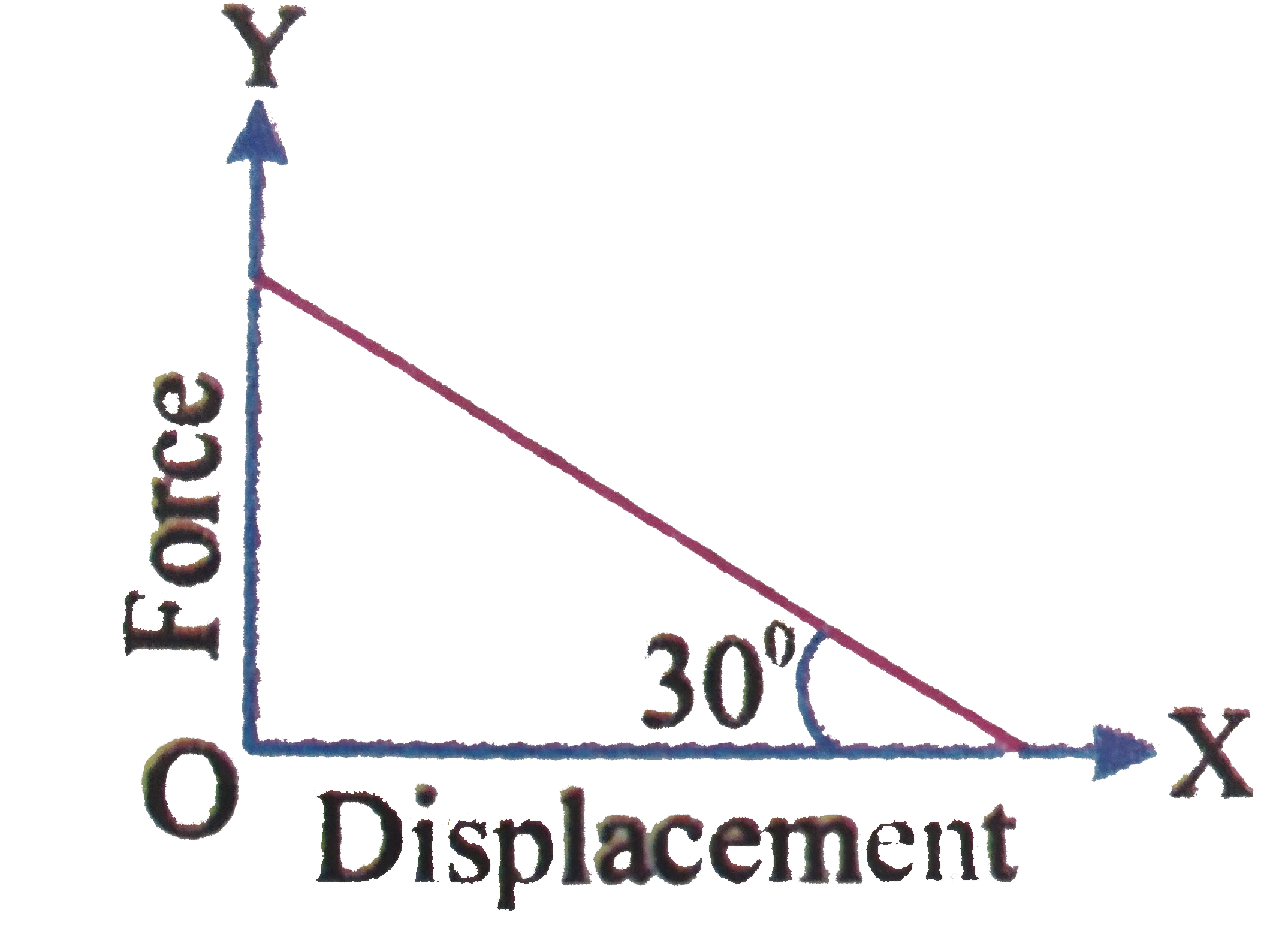 A√3B1√3C12D√32
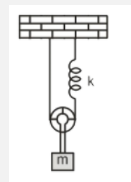
A√3B1√3C12D√32A mass M is suspended as shown in fig. The system is in equilibrium. Assume pulleys to be massless. K is the force constant of the spring.
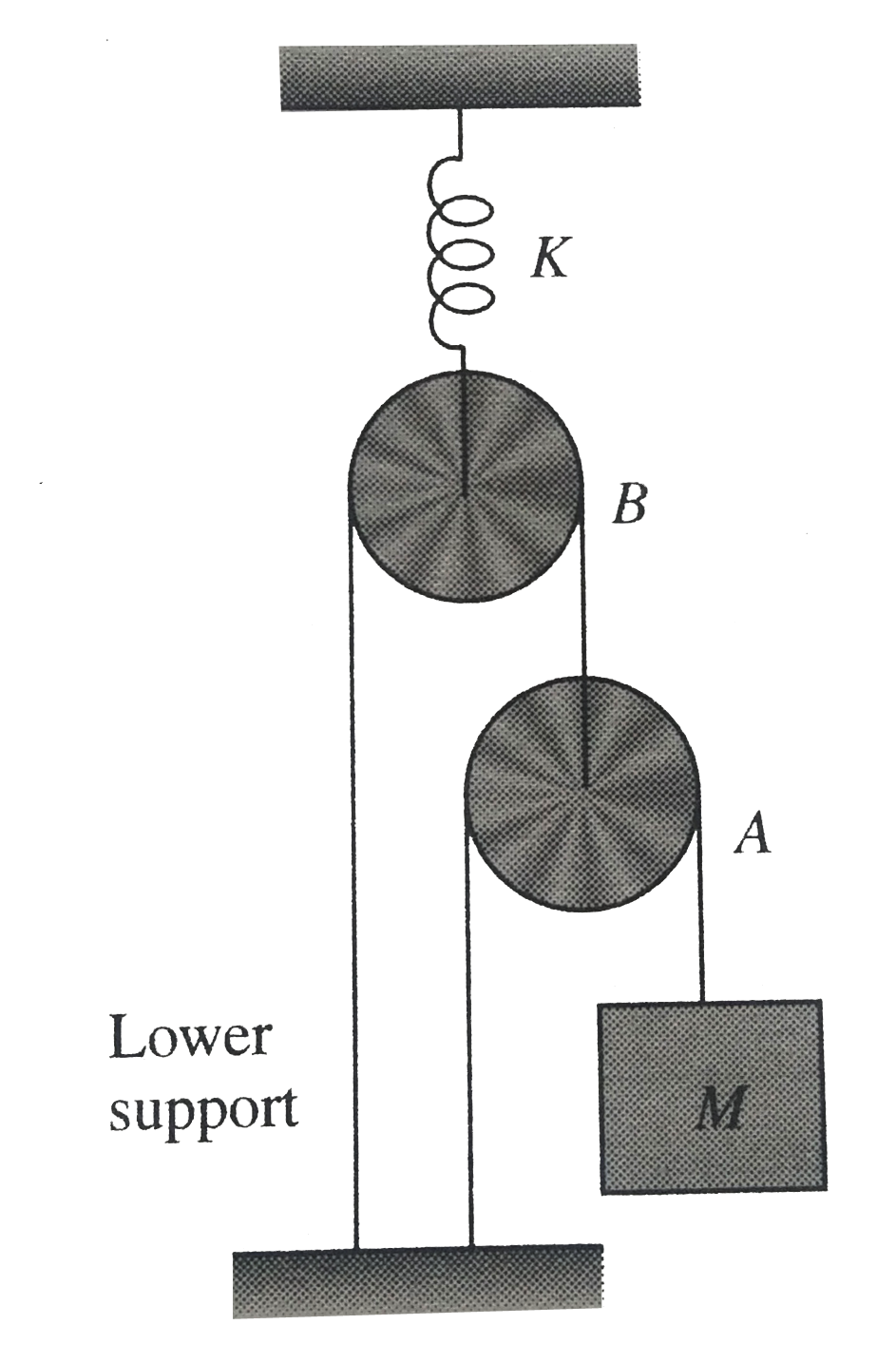
Find the net tension force acting on the lower support.AMgB2MgC3MgD4MgThe force F is given in terms of time t and displacement x by the equation F=AcosBx+CsinDt. The dimensions of DB are
AM∘L∘T∘BM∘L∘T−1CM∘L−1T∘DM∘L1T−1
Figure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
View SolutionFigure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

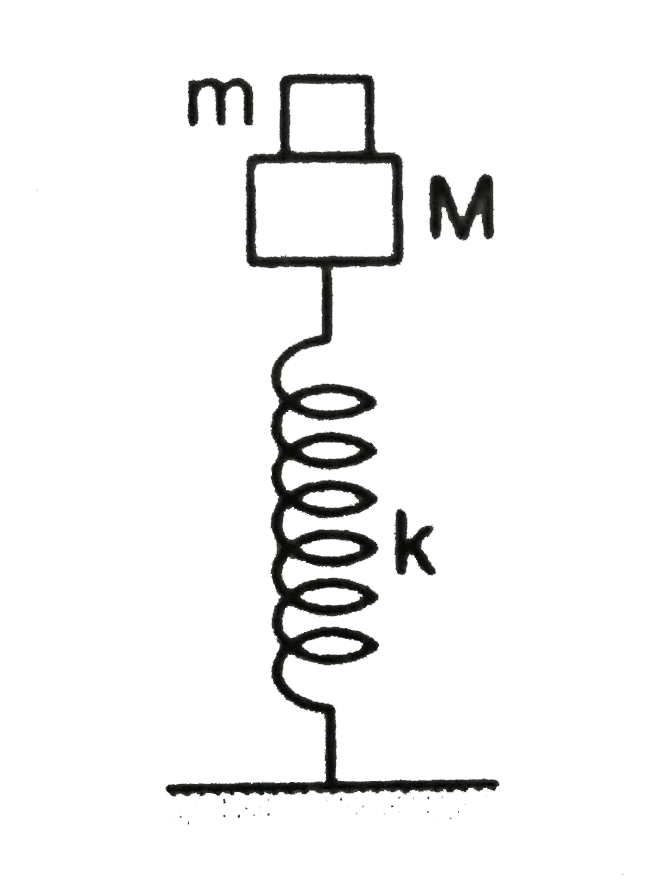
View SolutionA small block of mass m is kept on a bigger block of mass M which is attached to a vertical spring of spring constant k as shown in the figure. The system oscilates verticaly. a.Find the resultant force on the smaller block when it is displaced through a distance x above its equilibrium position. b. find the normal force on the smaller blok at this position. When is this force smallest smaller block at this position. When is this force smallest in magnitude? c. What can be the maximum amplitude with which the two blocks may oscillate together?
View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is
View Solution
