On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross sectiona area a. The height dference between them is equal to h. Find the resultant force of reaction of water flowing out of vessel.
Let A and B be two opening each off area a the velocity of water coming out of opening are VA and VB respectively. Volume of water emerging per second through A is aVA. Volume of water emerging per second through B is aVB
force of reaction due to water coming out at A is given by
FA= Rate of change of momentum per second at A
(aVAρ)VA=aρgVA
Similarly force of reaction at B is given by FB=aρV2B

Therefore net force on vessel is
F=FB−FA=aρ(V2B−V2A)..........i
Now, applying bernoulli's theorem at A and B, we get
pa+12ρV2A+(h2+h)ρg=p0+12ρV2B+ρgh........ii
where pa is atmospheric pressure
∴V2B−V2A=2gh
Substituting this value in eqn i we get F=aρ2gh
or F=2ρgah
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
On the opposite sides of a wide vertical vessel filled with water two identical holes are opened each having the cross-sectional area S=0.50cm2 the height difference between them is equal to Δh=51cm find the resultant force of reaction of the water flowing out of the vessel.
View SolutionOn the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View Solution
Knowledge Check
There are two holes one each along the opposite sides of a wide rectangular tak. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tak is filled with water. The net force on the tak in newton when water flows out of the holes is (density of water 1000kg/m3)
A100B200C300D400A cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
AH/4BH/2C3H/4DHA hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2
A flat wide and a high narrow box float in two identical vessels filled with water. The boxes do not sink when two identical heavy bodies of mass m each are placed into them.
In which vessel will the level of water be higher?
View SolutionA fixed container of height H with large cross-sectional area A is completely filled with water. Two small orifice of cross-sectional area a are made, one at the bottom and the other on the vertical side of the container at a distance H/2 from the top of the container find the time taken by the water level to reach a height of H/2 from the bottom of the container.
View SolutionThe side wall of a wide vertical vessel of height h=75cm a narrow slit (vertical) running all the way down to the bottom of the vessel.
The length of the slit is l=50cm and the width is b=1mm. With the slit closed, water is filled to the top. Find the resultant reaction force of water coming out as the slit is opened. brgt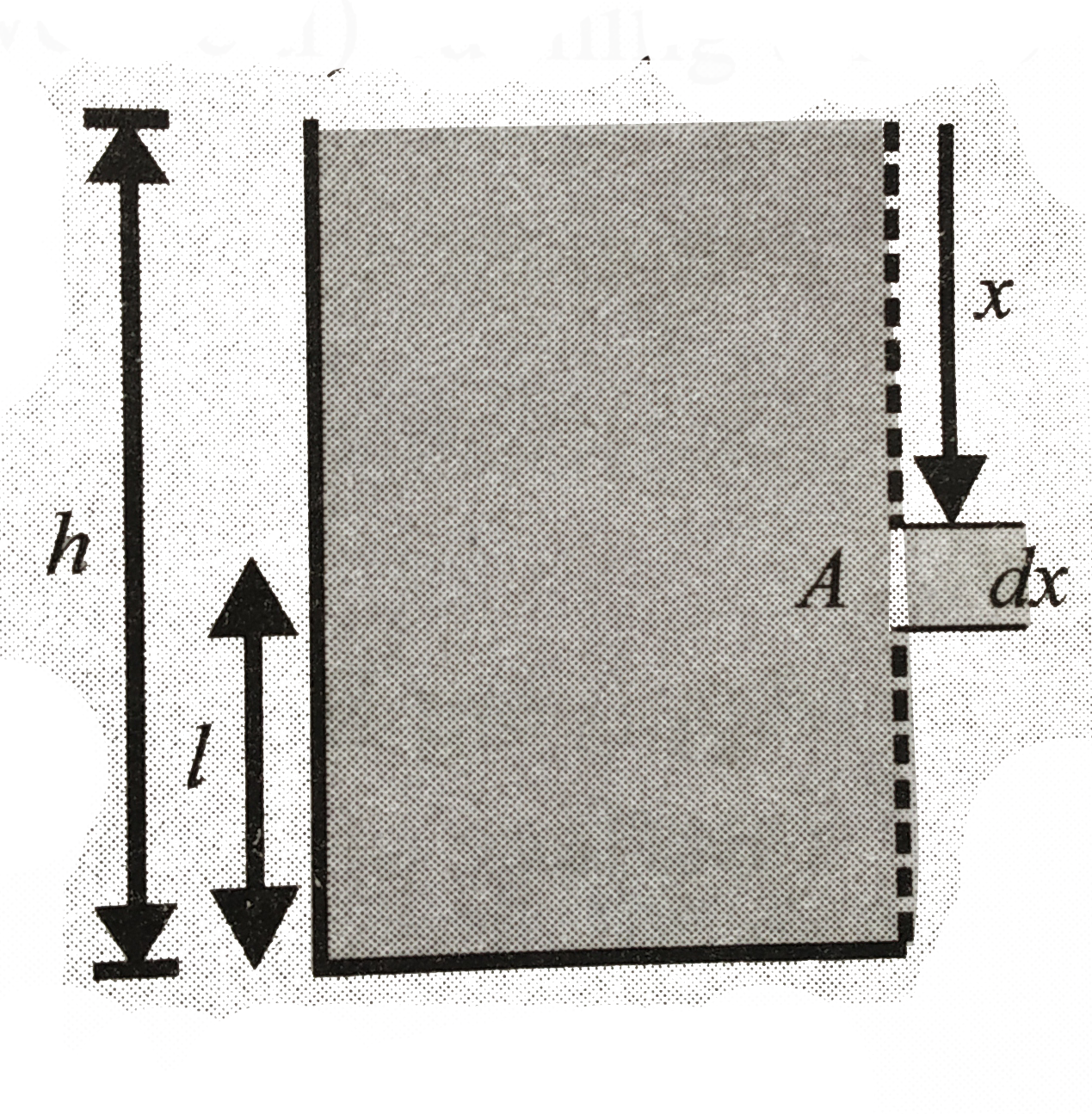
View SolutionWater drains out of a vessel filled with water upto height h through a hole of area A in t seconds.If the height of the water is 4 h then how much time will be required for the water to drain out ?[Assume A<<A0 (area of tank ) ]
View SolutionA tank of height H and base area A is half filled with water and there is a small orifice at the bottom and there is a heavy solid cylinder having base area A3 and height of the cylinder is same as that of the tak. The water is flowing out of the orifice. Here cylinder is put into the tank to increase the speed of water flowing out.
After long time, when the height of water inside the tank again becomes equal to H2, the solid cylinder is taken out. then the velocity of liquid flowing out of the orifice (just after removing the cylinder) will be
View Solution
