On the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
aρgh/2
3aρgh
aρgh
2aρgh
To solve the problem of finding the force on a vertical vessel filled with water with two identical holes on opposite sides, we can follow these steps:
1. Identify the Variables:
- Let the area of cross-section of each hole be a.
- The height difference between the two holes is h.
- The density of water is ρ.
2. Understanding the Flow:
- Water will flow out of both holes due to the difference in height, creating a pressure difference.
- We need to determine the velocities of water flowing out of each hole using Bernoulli's principle.
3. Apply Bernoulli's Equation:
- For the hole at the higher position (let's call it Hole A), the Bernoulli equation can be written as:
P0+ρgh+12ρv2A=P0+12ρv2B
- Here, P0 is the atmospheric pressure, g is the acceleration due to gravity, and vA and vB are the velocities of water exiting holes A and B respectively.
4. Relate the Velocities:
- Rearranging the Bernoulli equation gives:
ρgh=12ρv2B−12ρv2A
- This simplifies to:
gh=12(v2B−v2A)
5. Calculate the Force on Each Hole:
- The force exerted by the water flowing out of each hole can be expressed as:
FA=ρav2AandFB=ρav2B
- The net force on the vessel due to the water exiting both holes is:
Fnet=FB−FA=ρa(v2B−v2A)
6. Substituting the Velocity Difference:
- From the earlier relation, we know:
v2B−v2A=2gh
- Therefore, substituting this into the force equation gives:
Fnet=ρa(2gh)
7. Final Result:
- The resultant force on the vessel is:
F=2ρagh
Final Answer:
The force on the vessel is F=2ρagh.
---
- Let the area of cross-section of each hole be a.
- The height difference between the two holes is h.
- The density of water is ρ.
- Water will flow out of both holes due to the difference in height, creating a pressure difference.
- We need to determine the velocities of water flowing out of each hole using Bernoulli's principle.
- For the hole at the higher position (let's call it Hole A), the Bernoulli equation can be written as:
P0+ρgh+12ρv2A=P0+12ρv2B
- Here, P0 is the atmospheric pressure, g is the acceleration due to gravity, and vA and vB are the velocities of water exiting holes A and B respectively.
- Rearranging the Bernoulli equation gives:
ρgh=12ρv2B−12ρv2A
- This simplifies to:
gh=12(v2B−v2A)
- The force exerted by the water flowing out of each hole can be expressed as:
FA=ρav2AandFB=ρav2B
- The net force on the vessel due to the water exiting both holes is:
Fnet=FB−FA=ρa(v2B−v2A)
- From the earlier relation, we know:
v2B−v2A=2gh
- Therefore, substituting this into the force equation gives:
Fnet=ρa(2gh)
- The resultant force on the vessel is:
F=2ρagh
The force on the vessel is F=2ρagh.
Topper's Solved these Questions
Similar Questions
On the opposite sides of a wide vertical vessel filled with water, two identical holes are opened, each having cross sectiona area a. The height dference between them is equal to h. Find the resultant force of reaction of water flowing out of vessel.
View SolutionOn the opposite sides of a wide vertical vessel filled with water two identical holes are opened each having the cross-sectional area S=0.50cm2 the height difference between them is equal to Δh=51cm find the resultant force of reaction of the water flowing out of the vessel.
View Solution
Knowledge Check
A cylinderical vessel is filled with water up to height H. A hole is bored in the wall at a depth h from the free surface of water. For maximum range h is equal to
AH/4BH/2C3H/4DH
The vessel shown in the figure has two sections. The lower part is a rectangular vessel with area of cross-section A and height h. The upper part is a conical vessel of height h with base area A and top area a and the wals of the vessel are inclined at an angle 30∘ witht he vertical.A liquid of density ρ fills both the sections upto a height 2h. Neglect atmospheric pressure.AThe force F exerted by the liquid on the base of the vessel is 2hρg.(A+a)2BThe pressure P at the base of the vessel is 2hρg.AaCThe weight of the liquid W is greater than the force exerted by the liquid on the baseDthe walls of the vessel exert a downward force on the liquid.There are two holes one each along the opposite sides of a wide rectangular tak. The cross section of each hole is 0.01m2 and the vertical distance between the holes is one meter. The tak is filled with water. The net force on the tak in newton when water flows out of the holes is (density of water 1000kg/m3)
A100B200C300D400
The water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionTwo holes, each of area A=0.2cm2 are drilled in the wall of a vessel filled with water. The distances of the holes from the level of water are h and h+H. Find the point where the streams flowing out of the holes intersect. The level of water is maintained in the vessel by regulated supply.
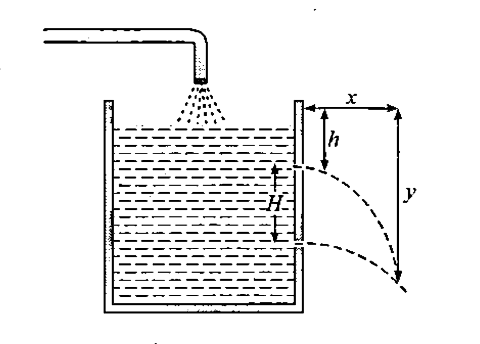
View SolutionAt the mount of the tap area of cross-section is 2.0cm2 and the speed of water is 3m/s. The area of cross-section of the water column 80 cm below the tap is (use g=10m/s2)
View SolutionA cylindrical tank having cross-sectional area A is filled with water to a height of 2.0 m. A circular hole of corss-section area is opened at a height of 75 cm from the bottom. If a/A=√0.2, then velocity with which waer emerges from the hole is
(g=9.8ms−2)
View SolutionAn open pan P filled with water (density ρm) is placed on one side of the pan as shown. If water depth is more then height of the block, then choose the correct statement.
View Solution
