On the surface of the moon , a cricket ball is hit at some angle with the horizontal . As the ball traveles through vecuume , determine which of the quantities will not change? (a) speed , (b) acceleration , (c) horizontal and vertical components of velocity and (d) resultant velocity .
To determine which of the quantities will not change when a cricket ball is hit at an angle on the surface of the moon, we need to analyze the motion of the ball in a vacuum. Let's break down the problem step by step:
Step 1: Understand the Environment
- The ball is projected on the moon, where there is no atmosphere. This means there are no resistive forces acting on the ball, such as air resistance.
Hint: Consider how the absence of air affects the motion of the ball.
Step 2: Identify the Forces Acting on the Ball
- The only force acting on the ball during its flight is the gravitational force of the moon. The gravitational acceleration on the moon is approximately g/6, where g is the acceleration due to gravity on Earth.
Hint: Think about how gravity influences the motion of the ball.
Step 3: Analyze the Components of Motion
- The motion of the ball can be broken down into horizontal and vertical components:
- Horizontal Component (ux): Since there is no acceleration in the horizontal direction, the horizontal component of velocity (ux) will remain constant.
- Vertical Component (uy): The vertical component of velocity (uy) will change due to the gravitational acceleration acting downward.
Hint: Remember that constant velocity means no change in speed or direction.
Step 4: Evaluate Each Quantity
1. Speed: The speed of the ball will change because the vertical component of velocity changes while the horizontal component remains constant.
2. Acceleration: The acceleration of the ball is constant at g/6 throughout its flight.
3. Horizontal and Vertical Components of Velocity:
- The horizontal component (ux) remains constant.
- The vertical component (uy) changes due to gravitational acceleration.
4. Resultant Velocity: The resultant velocity, which is the vector sum of the horizontal and vertical components, will change because the vertical component is changing.
Hint: Consider how changes in velocity components affect the overall velocity.
Conclusion
From the analysis:
- The quantity that does not change is acceleration. The horizontal component of velocity remains constant, but the vertical component changes, leading to a change in resultant velocity.
Final Answer
The quantity that will not change is (b) acceleration.
- The ball is projected on the moon, where there is no atmosphere. This means there are no resistive forces acting on the ball, such as air resistance.
- The only force acting on the ball during its flight is the gravitational force of the moon. The gravitational acceleration on the moon is approximately g/6, where g is the acceleration due to gravity on Earth.
- The motion of the ball can be broken down into horizontal and vertical components:
- Horizontal Component (ux): Since there is no acceleration in the horizontal direction, the horizontal component of velocity (ux) will remain constant.
- Vertical Component (uy): The vertical component of velocity (uy) will change due to the gravitational acceleration acting downward.
1. Speed: The speed of the ball will change because the vertical component of velocity changes while the horizontal component remains constant.
2. Acceleration: The acceleration of the ball is constant at g/6 throughout its flight.
3. Horizontal and Vertical Components of Velocity:
- The horizontal component (ux) remains constant.
- The vertical component (uy) changes due to gravitational acceleration.
4. Resultant Velocity: The resultant velocity, which is the vector sum of the horizontal and vertical components, will change because the vertical component is changing.
From the analysis:
- The quantity that does not change is acceleration. The horizontal component of velocity remains constant, but the vertical component changes, leading to a change in resultant velocity.
The quantity that will not change is (b) acceleration.
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - TOUGH & TRICKY PROBLEMS
14 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - NCERT FILE (Solved) NCERT (Textbook Exercises)
25 Videos
- MOTION IN A PLANE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A PLANE EXERCISE - PRACTICE PROBLEMS
2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - MODERN PUBLICATIONCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Chapter Practise Test
16 Videos
- MOTION IN A STRAIGHT LINE BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST
16 Videos
Similar Questions
In the above example , another cricket ball is hit with same speed and angle of projection on the earth . The horizontal range of this projectile as compared to that of the moon is (a) same , (b) less or (c) more .
View SolutionYou throw a ball toward a wall at speed 25.0 m/s and at angle θ0=40.0∘ above the horizontal. The wall is distance d = 22.0 m from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and ( c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory?

View Solution
Knowledge Check
The angle in which a cricket ball should be hit to travel maximum horizontal distance is
A60∘ with horizontalB45∘ with horizontalC30∘ horizontalD15∘ with horizontalA ball is thrown horizontally from top of a tower with velocity 30m/s. During its motion, at a particular point horizontal and vertical components of velocity are equal. The time to reach to the instant will be :
A3 secB4 secC5 secD6 secWe know how by neglecting the air resistance, the problems of projectile motion can be easily solved and analysed. Now we consider the case of the collision of a ball with a wall. In this case the problem of collision can be simplified by considering the case of elastic collision only. when a ball collides with a wass we divide its velocity into two components, one perpendiclar to the wall and other parallel to the wall. If the collision is elastic then the perpendicular component of velocity of the ball gets reversed with the same magnitude.

The other parallel component of velocity will remain constant if wall is given smooth.
Now, let us take a problem. Three balls A,B, and C are projected from ground with same speed at same angle with the horizontal. The ball A,B and C collide with the wall during their flight in air and all three collide perpendicularly with the wall as shown in figure.

The vertical component of velocity of balls wiht which they are projected isA20m/sB10m/sC10√3m/sDUndeterminable
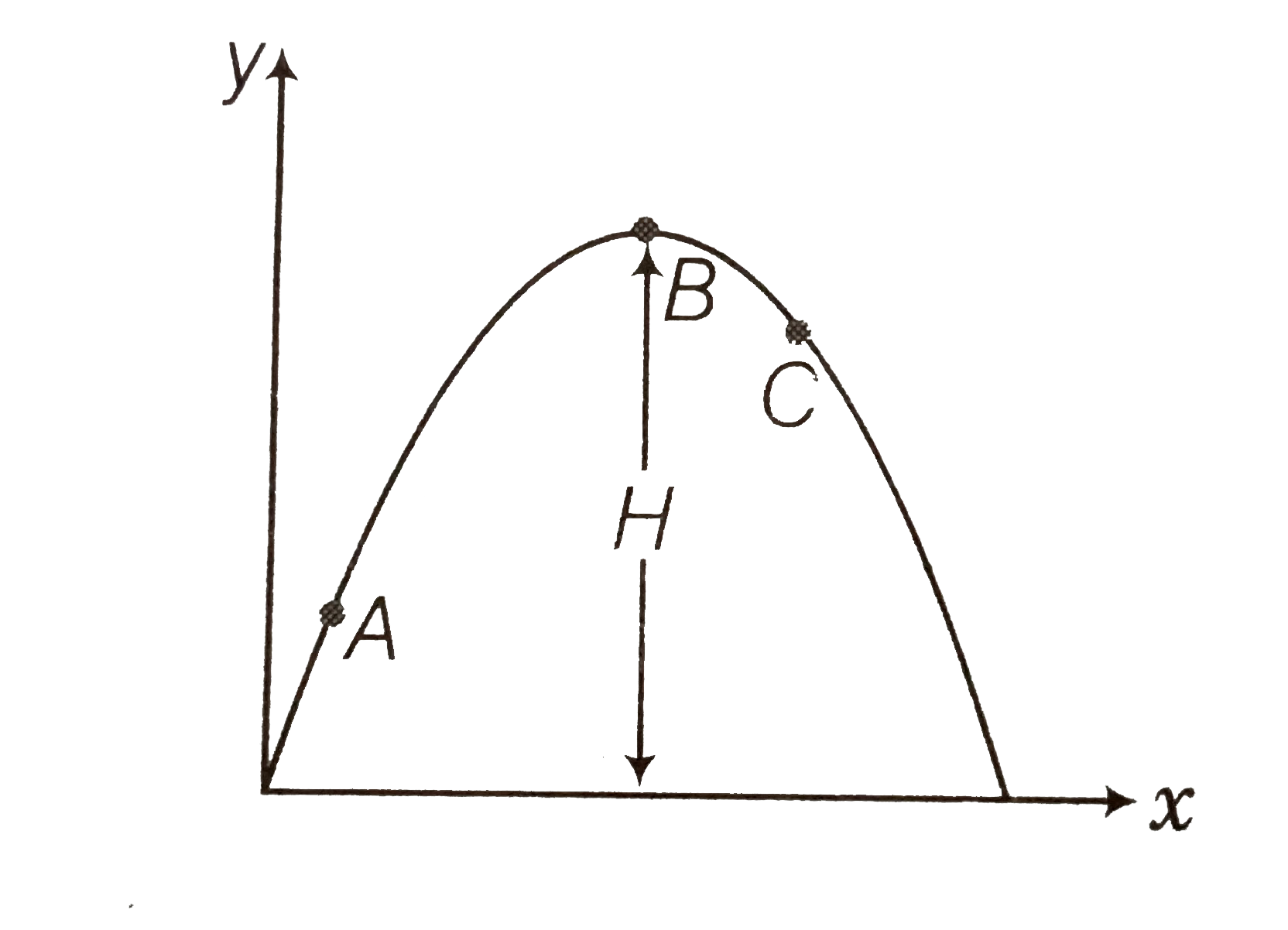
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure where x and y indicate horizontal and vertical directions, respectively . Shown in the diagram, direction of velocity and acceleration at points A, B and C.
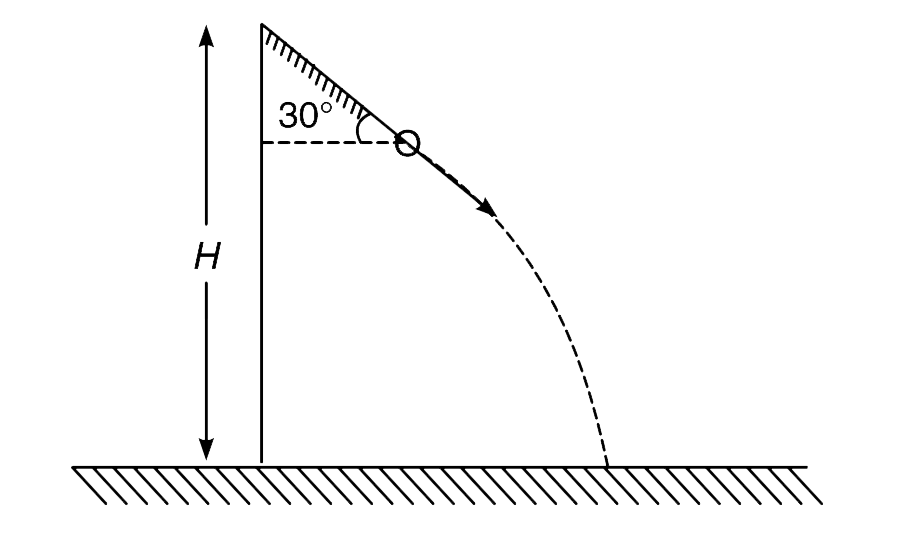
View SolutionStarting from a height H, a ball slips without friction, down a plane inclined at an angle of 30∘ to the horizontal (fig.). After leaving the inclined plane it fall under gravity on a parabolic path and hits the horizontal ground surface. The impact is perfectly elastic (It means that there is no change in horizontal component of ball’s velocity and its vertical velocity component gets inverted. There is no change in speed due to collision). Will the ball rise to a height equal to H or less than H after the impact ?
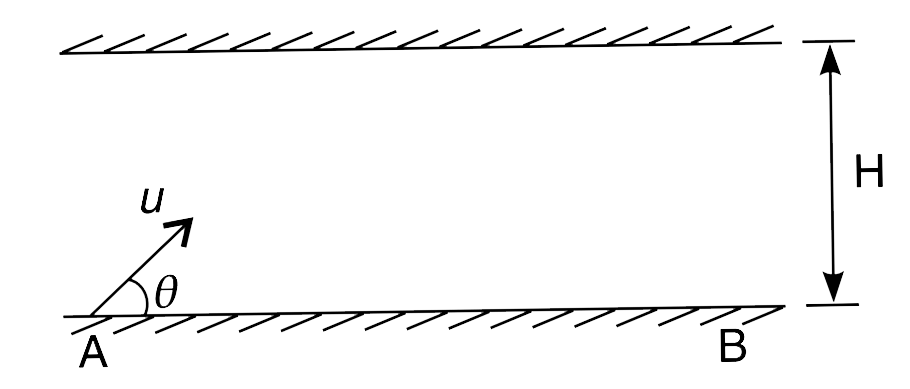
View SolutionA ball is projected from the floor of a long hall having a roof height of H=10m. The ball is projected with a velocity of u=25ms–1 making an angle of θ=37∘ to the horizontal. On hitting the roof the ball loses its entire vertical component of velocity but there is no change in the horizontal component of its velocity. The ball was projected from point A and its hits the floor at B. Find distance AB.
View SolutionA ball is projected with initial speed u at an angle θ above the horizontal . Calculate the time after which ball will be moving at right angle to its initial velocity.
View SolutionAssume that a ball is kicked at an angle of 60∘ with the horizontal, so if the horizontal component of its velocity is 19.6ms−1, determine its maximum height.
View Solution
