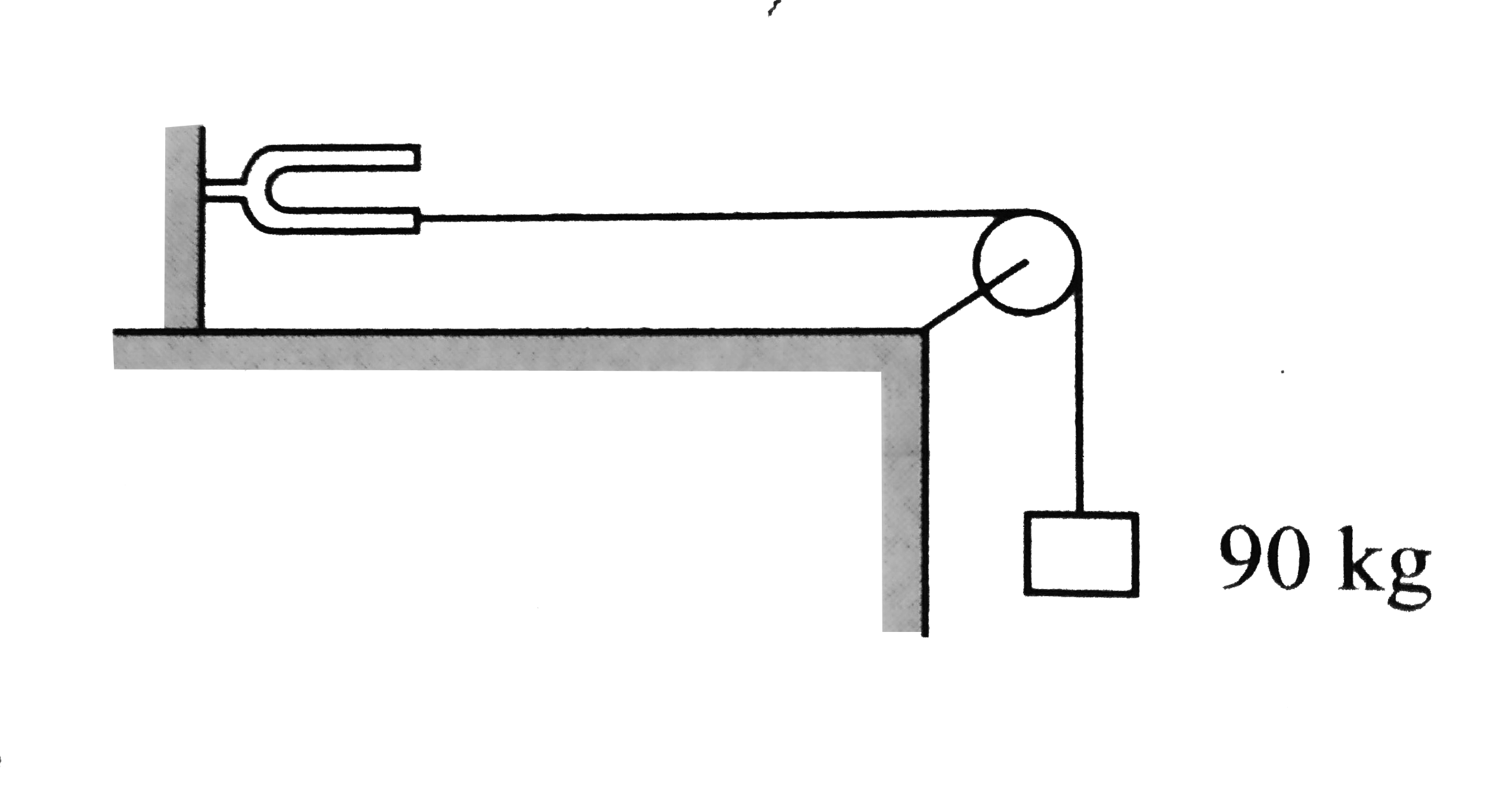
One end of a long string of linear mass density 10−2kgm−1 is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
θ=π/6
v=√T/μ=√9000.01=300m/s
frequency =150Hz
∴λ=vf=300150=2m
Then equation will be
y=Asin{2π(tT−xλ)+θ}
=5sin{2π(150t−x2)+π6}
=5sin{π(300t−x)+π6}
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct
62 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise 5.2
23 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
The speed of a wave in a medium is 960ms−1. If 3600 waves are passing through a point in the medium in one minute then calculate the wavelength.
View SolutionThe figure shows three progressive waves A, B and c. wahat canbe concluded from the figure that with respect to wave A?
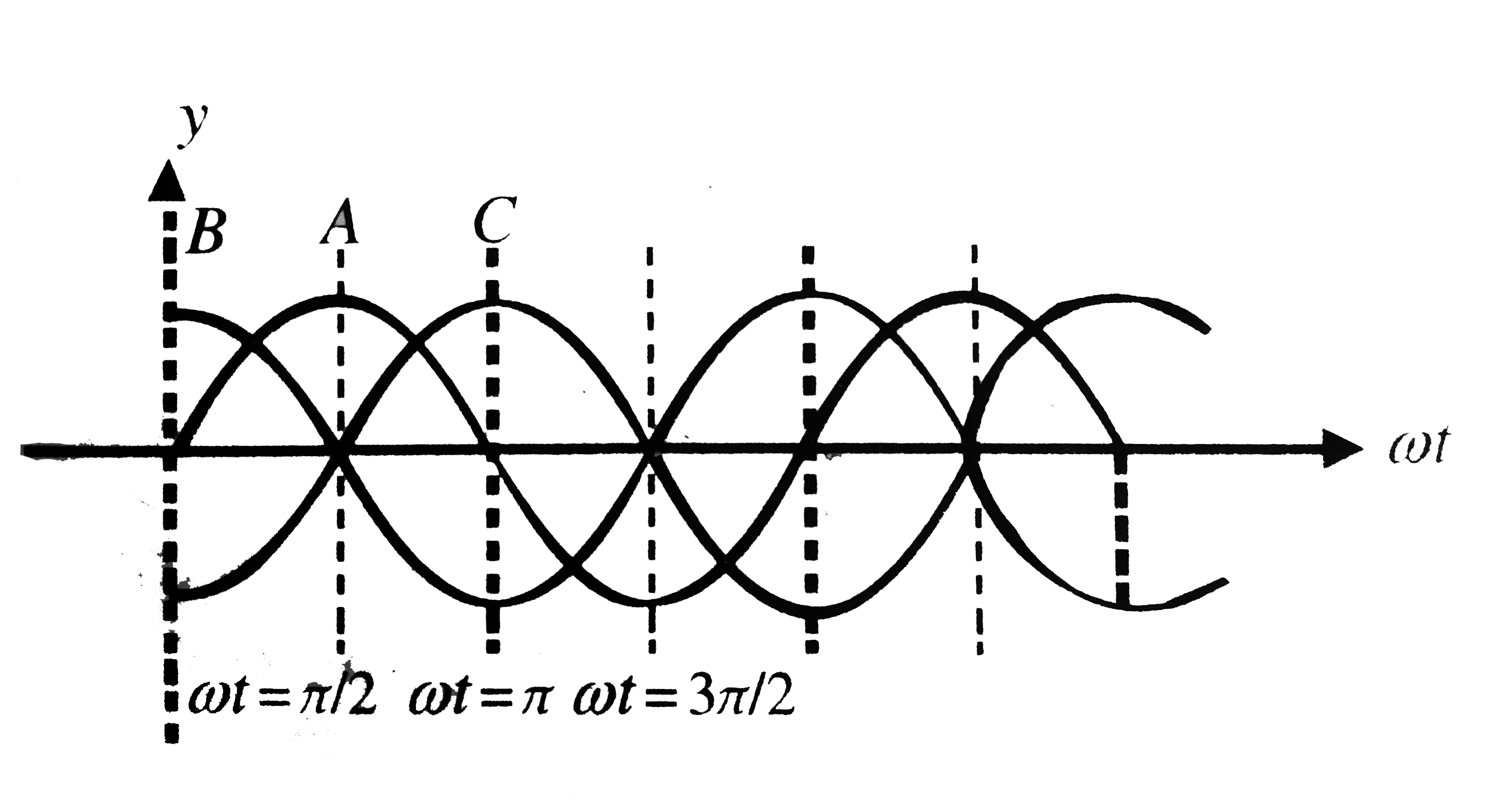
View SolutionA transverse wave is travelling along a string in the positive x-axis. The
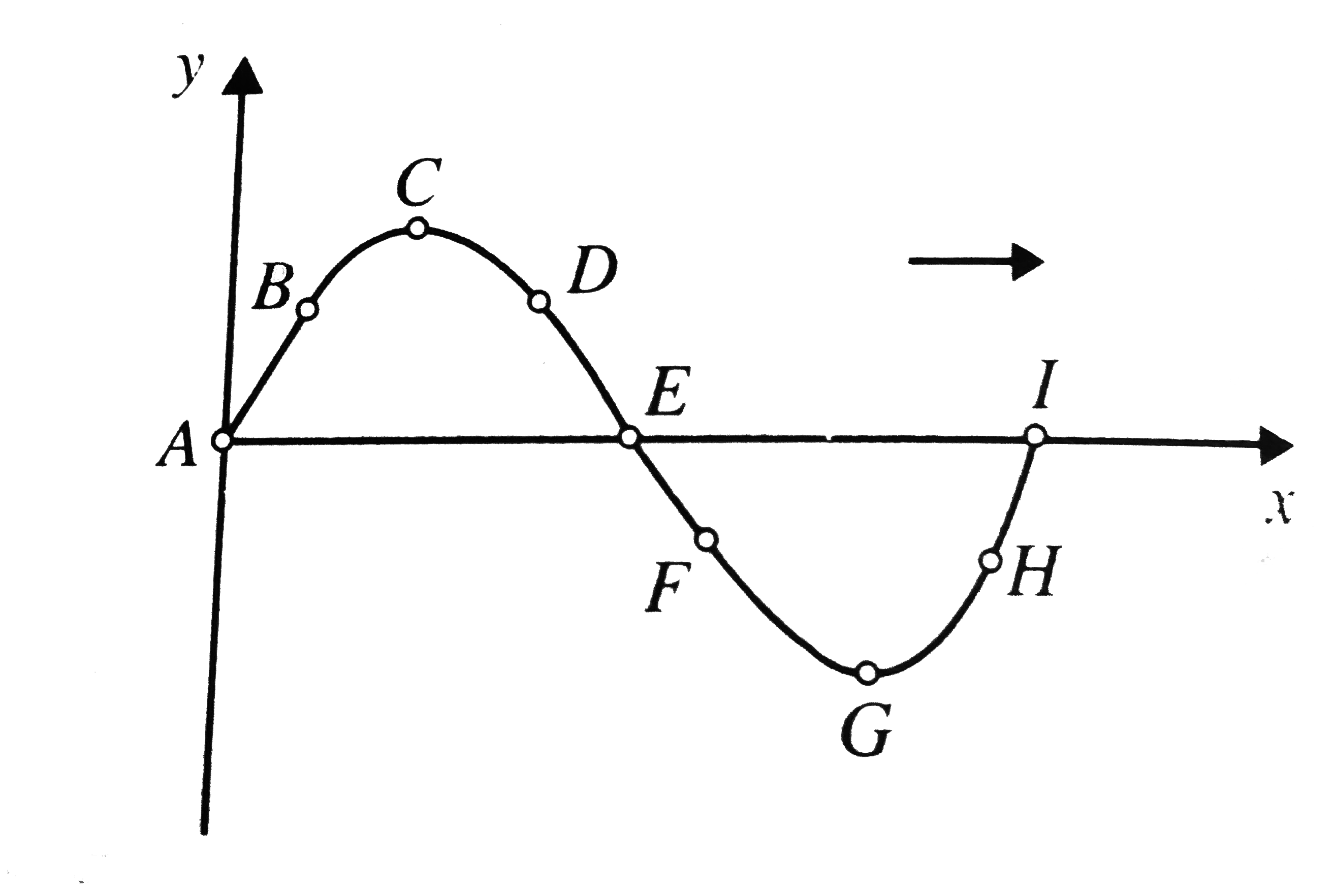
shows the photograph of the wave at an instant. Find
(a) the points moving upwards
(b) the points moving downwards
(c ) the points which have zero velocity
(d) the points which have maximum velocity
View SolutionConsider two hot bodies B1 and B2 which have temperature 100∘C and 80∘C respectively at t = 0. The temperature of surroundings is 40∘ C. The ratio of the respective rates of cooling R1 and R2 of these two bodies att=0 will be
View SolutionWhich of the following statements is/ are correct(Figure)
View SolutionOne end of a long string of linear mass density 10^(-2) kg m^(-1) is connected to an electrically driven tuning fork of frequency 150 Hz. The other end passes over a pulley and is tied to a pan containig a mass of 90 kg. the pulley end absorbs all the incoming energy so that reflected waves from this end have neglidible amplitude , At t =0, the left end (fork end ) of the string is at x=0 has a transverse displacement of 2.5 cm and is moving along positive y-direction. the amplitude of the wave is 5 cm. write down the transverse displacement y (in cetimetres) as function of x(in metres) and t (in seconds ) that describes the wave on the string.
View SolutionOne end of a long string of linear mass dnesity 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0 the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.
View SolutionThe linear mass density of the string shown in the figure is mu = 1 g//m . One end (A) of the string is tied to a prong of a tuning fork and the other end carries a block of mass M. The length of the string between the tuning fork and the pulley is L = 2.0 m . When the tuning fork vibrates, the string resonates with it when mass M is either 16 kg or 25 kg. However, standing waves are not observed for any other value of M lying between 16 kg and 25 kg. Assume that end A of the string is practically at rest and calculate the frequency of the fork.
View SolutionTwo masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionA light string passes over a frictionless pulley. To one of its ends a mass of 6 kg is attached. To its other end a mass of 10 kg is attached. The tension in the thread will be
View Solution8.0×10−3 kg m 1 रैखिक द्रव्यमान घनत्व की किसी लंबी डोरी का एक सिरा ( 256 Hz आवृत्ति के विद्युत चालित स्वरित्र द्विभुज से जुड़ा है । डोरी का दूसरा सिरा किसी स्थिर घिरनी के ऊपर गुजरता हुआ किसी तुला के पलड़े से बंधा है जिस पर 90 kg के बाट लटके है । घिरनी वाला सिरा सारी आवक ऊर्जा को अवशोषित कर लेता है जिसके कारण इस सिरे से परावर्तित तरंगो का आयाम नगण्य होता है । t=0 पर डोरी के बाएं सिरे (द्विभुज वाले सिरे ) x=0 पर अनुप्रस्थ विस्थापन शून्य है y=0 तथा वह y की धनात्मक दिशा के अनुदिश गतिशील है । तरंग का आयाम 5.0 cm है । डोरी पर इस तरंग का वर्णन करने वाले अनुप्रस्थ विस्थापन y को x तथा t के फलन के रूप में लिखिए ।
View SolutionOne end of a long string of linear mass density 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the leftend ( fork end )of the string x=0 has zero transverse displacement ( y = 0 ) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm.Write down the transverse displacement y as function of x and t that describes the wave on the string.
View SolutionOne end of a long string of linear mass density 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256 Hz. The other passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude . At t=0, the left end ( fork end) of the string x = 0 has zero transverse displacement ( y = 0 ) and is moving along positive y - direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as a function of x and t that describe the wave on the string.
View SolutionOne end of string which passes through pulley and connected to 10 kg mass at other end is pulled by 100 N force. Find out the acceleration of 10 kg mass. (g=9.8m/s2)
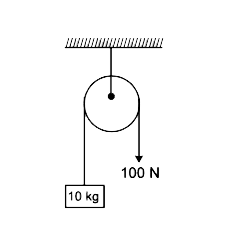
View SolutionTwo masses 2 kg and 4 kg are tied at the ends of a massless string and which is passing over a frictionless pulley. The tension in the string is
View SolutionOne end of a long string of linear mass density 8.0×10−3kgm−1 is connected to an electrically driven tuning fork of frequency 256Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At t=0, the left end (fork end) of the string x=0 has zero transverse displacement (y=0) and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describes the wave on the string.
View Solution
