One end of a spring is rigidly fixed. A block attached to the free end of the spring is pulled through a distance x0. On releasing the block, its amplitude of motion cannot exceed ±x0. Why?
When the spring is stretched by x0 its P.E.
=12kx20
where k is spring constant. At x>x0. PE will be greater than 12kx20. Therefore , its KE=(12kx20−12kx2) would be negative, which is not possible. Therefore, amplitude of motino cannot exceed ±x0.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.54videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Short Answer Question52videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - solved examples73videos
WORK, ENERGY AND POWER
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
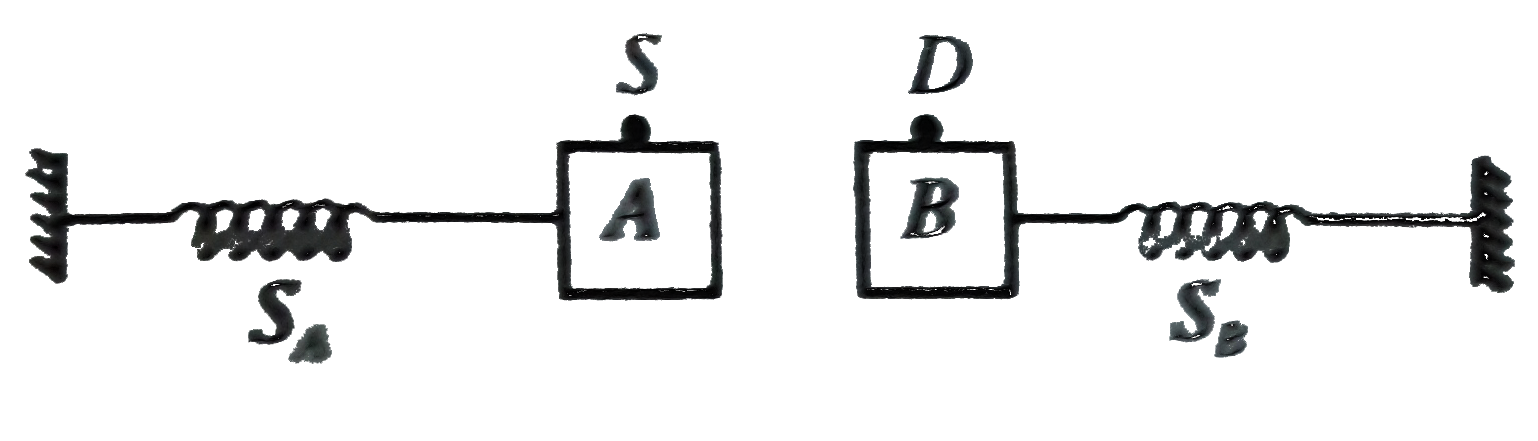
A source S emitting sound of 300 Hz is fixed of block A which is attached to free end of a spring SA as shown in the figure. The detector D fixed on block B attached to the free end of spring SB detects this sound.
The blocks A and B are simultaneously displaced towards each other through of 1.0 m and then left to vibrate. Find the maximum and minimum frequencies of sound detected by D if the vibrational frequency of each block is 2 Hz (velocity of sound is 340 m/s).View Solution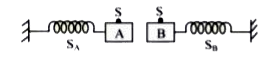
A source s emitting sound of 400 Hz is fixed on block A which is attached to free end of a spring SA. The detector D fixed on block B attached to the free end of spring SB detects this sound. The blocks A and B are simultaneously displaced towards each other through a distance of 1. Om and then left to vibrate. If vibrational frequency of each block is 3 Hz, the maximum frequencies of sound detected by Dis n hz. Then, what is the value of n10? (υsound = 340m/s)View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to
 A4π3√mkBπ√2√mkC2π3√mkDNone of these
A4π3√mkBπ√2√mkC2π3√mkDNone of these - Question 2 - Select One or More
A spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
Athe block will perform SHM of amplitude 5cmBthe block will have maximum velocity 30√5cm/sCthe block will have maximum acceleration 15m/s2Dthe minimum elastic potential energy of the spring will be zero - Question 3 - Select One
A source S emitting sound of frequency 300Hz is fixed on block A which is attached to the free end of a spring SA as shown in figure. The detector D fixed on block B attached to free end of spring SB detects this sound. The blocks A and B are simultaneously displaced towards each other through a distance of 1.0m and then left to vibrate. The maximum and minimum frequencies of sound detected by D, if the vibrational frequency of each block is 2Hz are (Velocity of sound v=340m/s)
 A378.6Hz, 223HzB323Hz, 278.6HzC178Hz, 276HzD420Hz, 220Hz
A378.6Hz, 223HzB323Hz, 278.6HzC178Hz, 276HzD420Hz, 220Hz
One end of a fixed spring is pulled by an average force of 10N through a distance of 5cm, find the work done by the spring.
View SolutionOne end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m=1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x=10+3sin(10t). Here, t is in second and x in cm. Another block of mass M=3kg, moving towards the origin with velocity 30cm/s collides with the block performing SHM at t=0 and gets stuck to it. Calculate

(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.View SolutionOne end of a spring is fixed to the ceiling and other end is attached to a block. The block is released when spring is relaxed. The product of time period and amplitude is 8 S.I. units. If spring is cat in two equal parts and the two springs are attached to the block as shown in figure. The block is released when both springs are relaxed. Now find the product of time period and amplitude in S.I. units.
'(##CEN_KSR_PHY_JEE_C16_E01_028_Q12##)'View SolutionA block of mass 1 kg is attached to one end of a spring of force constant k = 20 N/m. The other end of the spring is attached to a fixed rigid support. This spring block system is made to oscillate on a rough horizontal surface (μ=0.04). The initial displacement of the block from the equilibrium position is a = 30 cm. How many times the block passes from the mean position before coming to rest ? (g=10m/s2)
View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
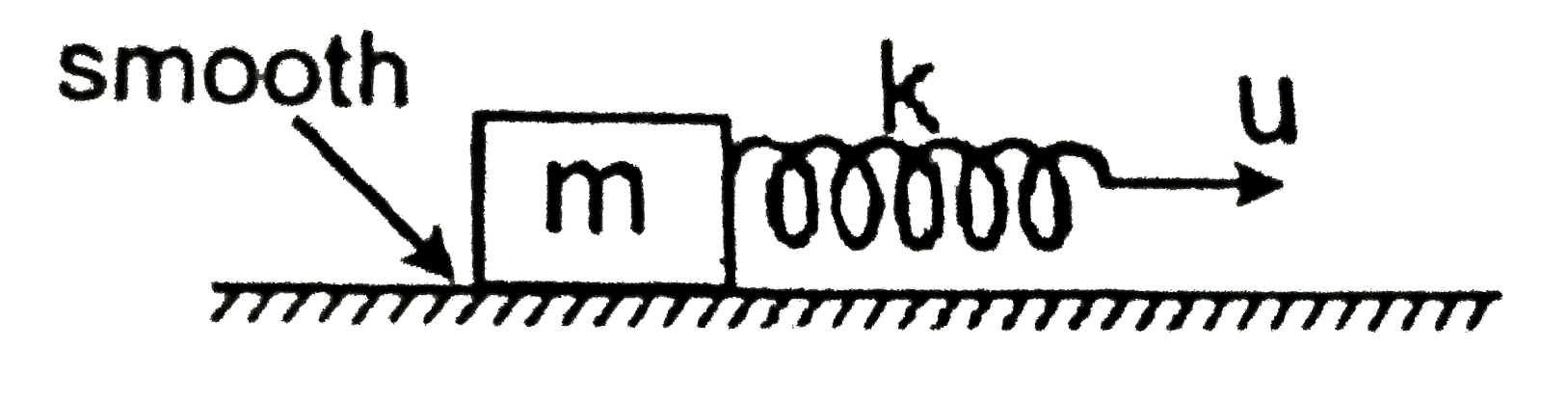 View Solution
View Solution

