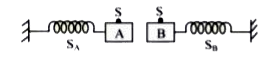
A source s emitting sound of 400 Hz is fixed on block A which is attached to free end of a spring SA. The detector D fixed on block B attached to the free end of spring SB detects this sound. The blocks A and B are simultaneously displaced towards each other through a distance of 1. Om and then left to vibrate. If vibrational frequency of each block is 3 Hz, the maximum frequencies of sound detected by Dis n hz. Then, what is the value of n10? (υsound = 340m/s)
The correct Answer is:44.80
ω=2πυ=2π(3)=6π
∴ω=18.85rades−1
Maximum speed of motion of ∣∣ɛA∣∣and∣∣ɛB∣∣=Aω
fmax=(v+vBV−VA)f=(340+Aω340−Aω)f
(340+18.85340−18.85)400
=(358.58321.15)×400
1.12×400
fmax=448Hz
Topper's Solved these Questions
Similar Questions
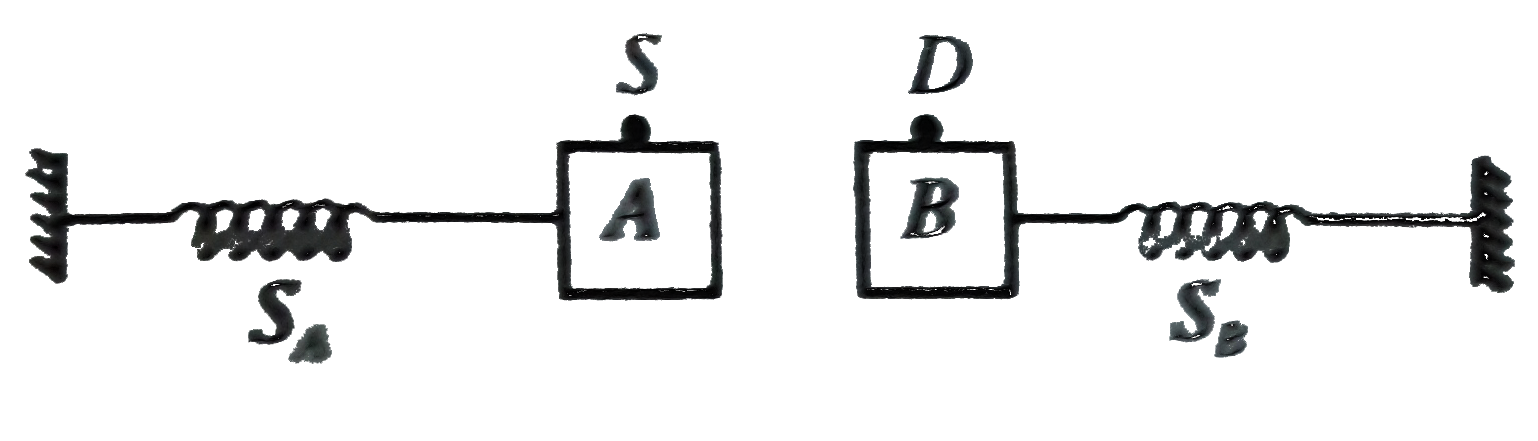
A source S emitting sound of 300 Hz is fixed of block A which is attached to free end of a spring SA as shown in the figure. The detector D fixed on block B attached to the free end of spring SB detects this sound.
The blocks A and B are simultaneously displaced towards each other through of 1.0 m and then left to vibrate. Find the maximum and minimum frequencies of sound detected by D if the vibrational frequency of each block is 2 Hz (velocity of sound is 340 m/s).View Solution-
A source S emitting sound of 300 Hz is fixed of block A which is attached to free end of a spring SA as shown in the figure. The detector D fixed on block B attached to the free end of spring SB detects this sound.
The blocks A and B are simultaneously displaced towards each other through of 1.0 m and then left to vibrate. Find the maximum and minimum frequencies of sound detected by D if the vibrational frequency of each block is 2 Hz (velocity of sound is 340 m/s).View Solution
Knowledge Check
- Question 1 - Select One
A source S emitting sound of frequency 300Hz is fixed on block A which is attached to the free end of a spring SA as shown in figure. The detector D fixed on block B attached to free end of spring SB detects this sound. The blocks A and B are simultaneously displaced towards each other through a distance of 1.0m and then left to vibrate. The maximum and minimum frequencies of sound detected by D, if the vibrational frequency of each block is 2Hz are (Velocity of sound v=340m/s)
A378.6Hz, 223HzB323Hz, 278.6HzC178Hz, 276HzD420Hz, 220Hz - Question 2 - Select One
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2km - Question 3 - Select One
A block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
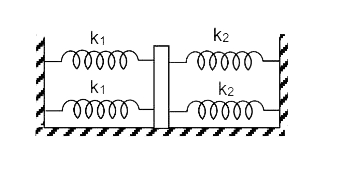A√2(k1+k2)xmB√3(k1+k2)x22mC√(k1k2)3(k1+k2)mD√(k1+k2)x(k1+k2)m
A source S emitting sound of 300Hz is fixed on block A which is attache to free end of a spring SA as shown in figure. The detector D fixed on block B attached to free end of spring SB detects this sound. The blocks A and B simultaneously displaced towards each other thrugh a distance of 2.0m and then left to vibrate. If the product of maximum and minimum freuquencies of sound detected by D is K+104sec−2. Find K. Given the vibrational frequencies of each block is 5/πHz. speed of sound in air =300m/s
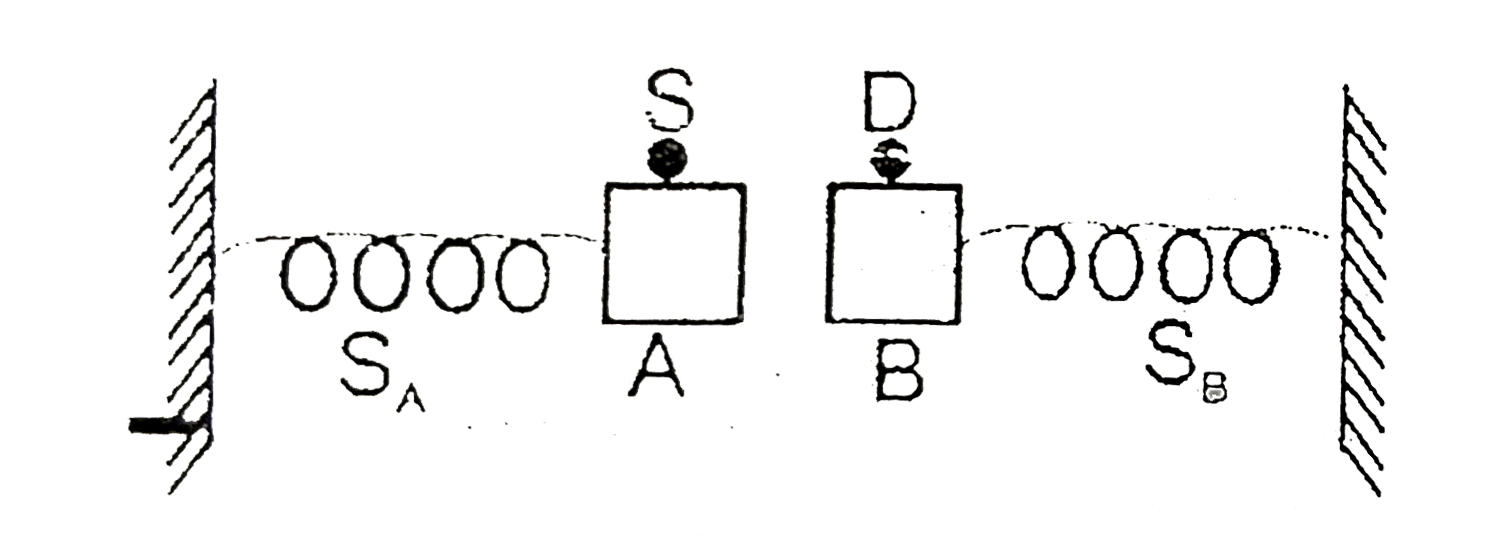
View SolutionA source S emitting sound of 300Hz is fixed on block A which is attache to free end of a spring SA as shown in figure. The detector D fixed on block B attached to free end of spring SB detects this sound. The blocks A and B simultaneously displaced towards each other thrugh a distance of 2.0m and then left to vibrate. If the product of maximum and minimum freuquencies of sound detected by D is K+104sec−2. Find K. Given the vibrational frequencies of each block is 5/πHz. speed of sound in air =300m/s
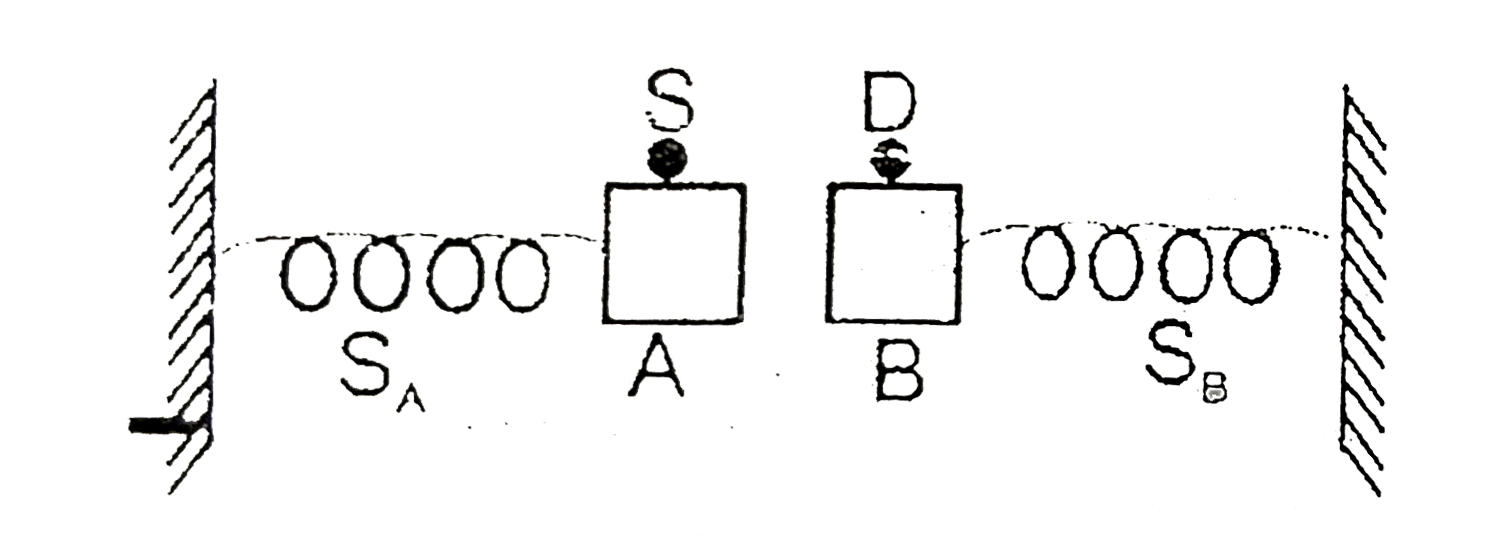
View Solution-
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beView Solution One end of a spring is rigidly fixed. A block attached to the free end of the spring is pulled through a distance x0. On releasing the block, its amplitude of motion cannot exceed ±x0. Why?
View SolutionA block of mass m is attached to four unstretched massless springs of spring constant k1andk2 as shown in figure. The block is displaced towards right through distance x and is released. Speed of block when displacement of block is x/2 from mean position is :
View Solution