One end of conducting rod is maintained at temperature and at the other end ice is melting at . The rate of melting of ice is doubled if:
The temperature is made and the area of cross-section of the rod is doubled
The temperature is made and length of the rod is made of four times
Area of cross section of rod is halved and length is doubled
The temperature is made and area of cross-section of rod and length both are doubled
The correct Answer is:D
In steady state of a rod the rate of heat conduction is given as so to double the rate option (D) iscorrect.
Topper's Solved these Questions
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Numerical MCQs Single Options Correct
94 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Advance MCQs with One or More Option Correct
20 Videos
- HEAT TRANSFER BOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT TRANSFER EXERCISE - Discussion Question
26 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
- Kinetic Theory of Gases and Gas LawsBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - Kinetic Theory of Gases and Gas LawsEXERCISE - Unsolved Numerical Problems for Preparation of NSEP, INPhO & IPhO
64 Videos
Similar Questions
One end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
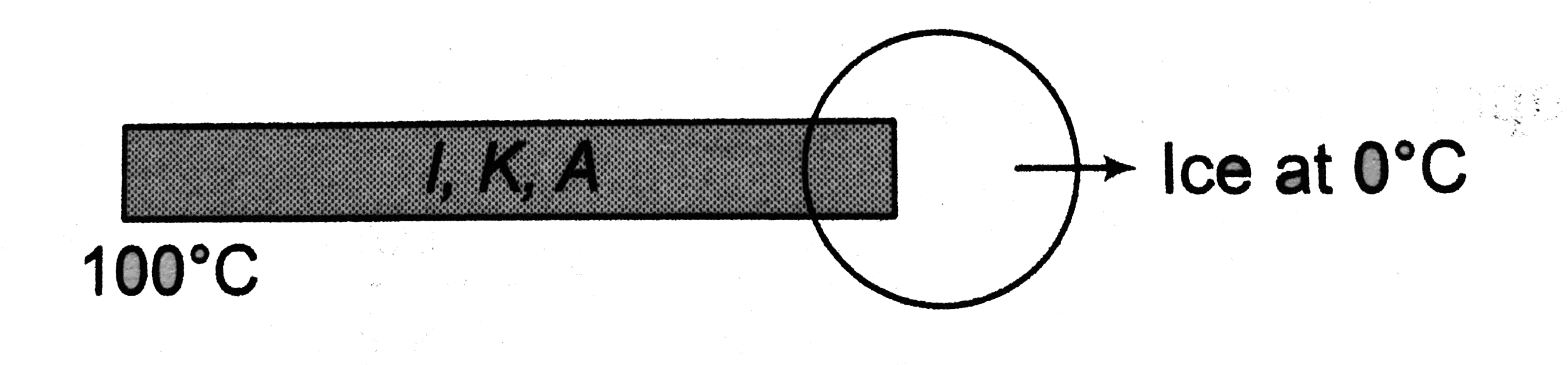 .
.
View SolutionThe container A contains ice at O∘C. A conducting uniform rod PQ of length 4R is used to transfer heat to the ice in the container. The end P of the rod is maintained at 100∘C and the other end Q is kept inside container A. The complete ice melts in 23 minutes. In another experiment, two conductors in shape of quarter circle of radii 2R and R are welded to the conductor PQ at M and N respectively and their other ends are inserted inside the container A. All conductors are made of same material and have same cross sectional area. Once again the end P is maintained at 100∘C and this time the com- plete ice melts in t min- ute. Find t. Assume no heat loss from the curved surface of the rods. [Take π≅3.0]
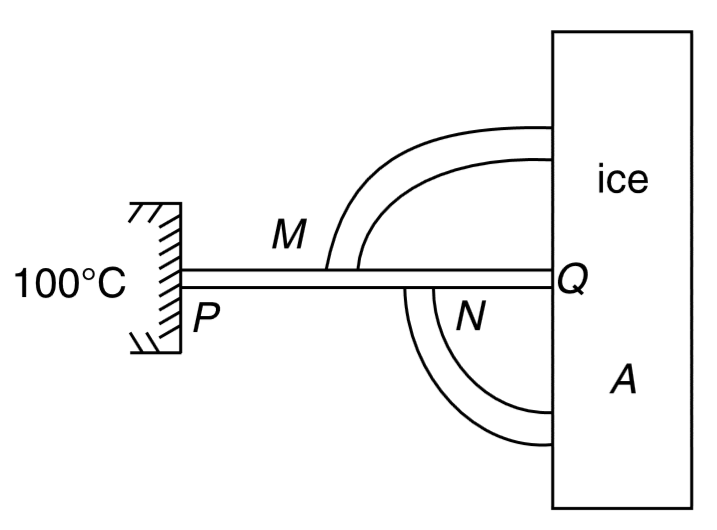
View Solution
Knowledge Check
The ΔG in the process of melting of Ice at −15∘C is
AΔG<0BΔG>0CΔG=0Dnone of theseWhen 1 g of ice melts at 0∘C
A80 cal of heat is liberatedB80 cal of heat is absorbedCno heat is requiredDnone of theseWhen ice melts at 1∘C :
Aan increase in entropyBa decrease in enthalpyCa decrease in free energyDprocess is spontaneous
One end of 0.5 m long metal rod is in steam at 100∘C and the other end is put in ice at 0∘C. If ice melts at the rate of 10 g/min, calculate the thermal conductivity of the metal. Take, cross sectional area of rod=2πcm2 . Latent ice of heat = 80 cal/g
View SolutionOne end of a steel rod (K=46Js−1m−1^(@)C^(-1)of≤n>h1.0m is kept in ice at 0∘C and the other end is kept in boiling water at 100^(@)C.Theareaofcrosssectionoftherodis0.04cm^(2).As∑∈gnoheatloss→theatmosphere,f∈dthemassoftheiceme<∈gpersecond.Latentheatoffusionofice=3.36xx10^(5)Jkg^(-1) .
View SolutionTwo identical rods are connected in parallel. One end of the rods is maintained at 100∘C and other end is kept in 0∘C ice . The rate at which the ice melts is Q1 gm/sec . Now the rods are connected in series . The ends are again maintained at 100∘C and kept in 0∘C ice . Now the rate at which ice melts is Q2 gm/sec . Then Q2/Q1 is
View SolutionDuring the melting of ice, temperature .
View SolutionOne end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
View Solution
