One end of conducting rod is maintained at temperature 50∘C and at the other end ice is melting at 0∘C. The rate of melting of ice is doubled if:
the temperature is made 200∘C and the area of cross-section of the rod is doubled
the temperature is made 100∘C and length of the rod is made four times
area of cross-section of rod is halved and length doubled
the temperature is made 100∘C and area cross-section of rod and length both are doubled
The correct Answer is:D
To solve the problem, we need to analyze the heat transfer through the conducting rod and how changes in temperature, area of cross-section, and length affect the rate of heat transfer.
1. Understand the Heat Transfer Formula:
The rate of heat transfer (Q) through a conducting rod is given by the formula:
Q=K⋅A⋅(T1−T2)L
where:
- K = thermal conductivity of the material
- A = area of cross-section of the rod
- T1 = temperature at one end of the rod
- T2 = temperature at the other end of the rod
- L = length of the rod
2. Initial Conditions:
In our case:
- T1=50∘C
- T2=0∘C
- The initial heat transfer rate Q can be expressed as:
Q=K⋅A⋅(50−0)L=K⋅A⋅50L
3. Evaluate Each Option:
We will evaluate each option to see if it results in doubling the rate of melting of ice (i.e., Q=2Q).
Option 1: Temperature is made 200∘C and area is doubled.
- New conditions:
Q1=K⋅(2A)⋅(200−0)L=K⋅2A⋅200L=K⋅400AL
- Comparing with initial Q:
Q1=8Q(since 400A/L=8⋅50A/L)
- Conclusion: This option is incorrect (rate is 8 times).
Option 2: Temperature is made 100∘C and length is made 4 times.
- New conditions:
Q2=K⋅A⋅(100−0)4L=K⋅A⋅1004L=K⋅25AL
- Comparing with initial Q:
Q2=12Q(since 25A/L=12⋅50A/L)
- Conclusion: This option is incorrect (rate is half).
Option 3: Area of cross-section is halved and length is doubled.
- New conditions:
Q3=K⋅(A2)⋅(50−0)2L=K⋅25A2L
- Comparing with initial Q:
Q3=14Q(since 25A/L=14⋅50A/L)
- Conclusion: This option is incorrect (rate is one-fourth).
Option 4: Temperature is made 100∘C and both area and length are doubled.
- New conditions:
Q4=K⋅(2A)⋅(100−0)2L=K⋅2A⋅1002L=K⋅100AL
- Comparing with initial Q:
Q4=2Q(since 100A/L=2⋅50A/L)
- Conclusion: This option is correct (rate is doubled).
Final Answer:
The rate of melting of ice is doubled if the temperature is made 100∘C and both the area of cross-section and length of the rod are doubled (Option 4).
The rate of heat transfer (Q) through a conducting rod is given by the formula:
Q=K⋅A⋅(T1−T2)L
where:
- K = thermal conductivity of the material
- A = area of cross-section of the rod
- T1 = temperature at one end of the rod
- T2 = temperature at the other end of the rod
- L = length of the rod
In our case:
- T1=50∘C
- T2=0∘C
- The initial heat transfer rate Q can be expressed as:
Q=K⋅A⋅(50−0)L=K⋅A⋅50L
We will evaluate each option to see if it results in doubling the rate of melting of ice (i.e., Q=2Q).
- New conditions:
Q1=K⋅(2A)⋅(200−0)L=K⋅2A⋅200L=K⋅400AL
- Comparing with initial Q:
Q1=8Q(since 400A/L=8⋅50A/L)
- Conclusion: This option is incorrect (rate is 8 times).
- New conditions:
Q2=K⋅A⋅(100−0)4L=K⋅A⋅1004L=K⋅25AL
- Comparing with initial Q:
Q2=12Q(since 25A/L=12⋅50A/L)
- Conclusion: This option is incorrect (rate is half).
- New conditions:
Q3=K⋅(A2)⋅(50−0)2L=K⋅25A2L
- Comparing with initial Q:
Q3=14Q(since 25A/L=14⋅50A/L)
- Conclusion: This option is incorrect (rate is one-fourth).
- New conditions:
Q4=K⋅(2A)⋅(100−0)2L=K⋅2A⋅1002L=K⋅100AL
- Comparing with initial Q:
Q4=2Q(since 100A/L=2⋅50A/L)
- Conclusion: This option is correct (rate is doubled).
The rate of melting of ice is doubled if the temperature is made 100∘C and both the area of cross-section and length of the rod are doubled (Option 4).
Topper's Solved these Questions
Similar Questions
When ice melts at 1∘C :
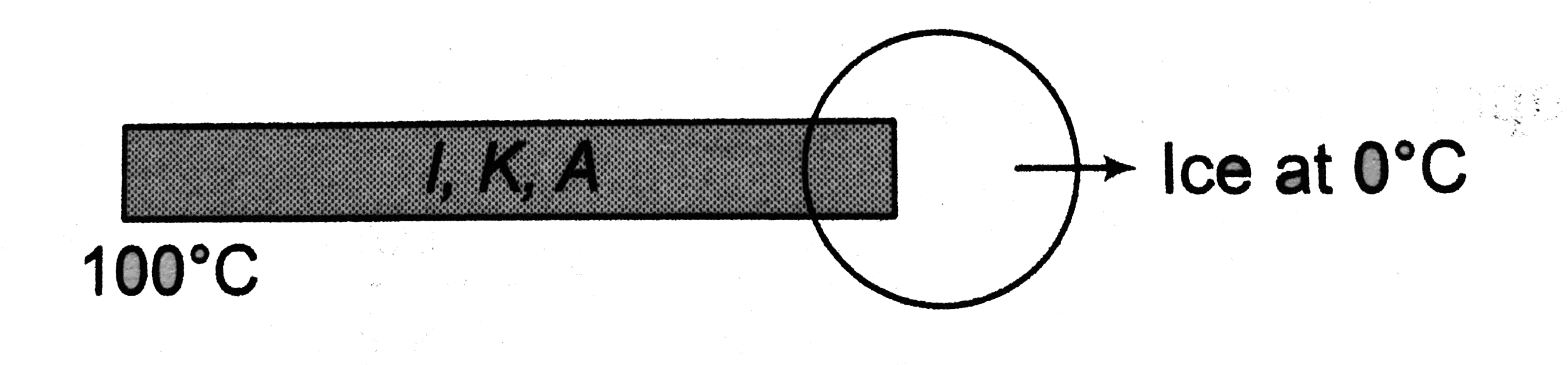
View SolutionOne end of the rod of length l, thermal conductivity K and area of cross-section A is maintained at a constant temperature of 100∘C. At the other end large quantity of ice is kept at 0∘C . Due to temperature difference, heat flows from left end to right end of the rod. Due to this heat ice will start melting. Neglecting the radiation losses find the expression of rate of melting of ice.
 .
.
View Solution
Knowledge Check
The temperature of pure melting ice is :
A0∘CB100∘CC95∘CD98.6∘F
The value of absolute temperature at which ice starts melting is
View SolutionThe two ends of a metal rod are maintained at temperature 100∘C and 110∘C. The rate of heat flow in the rod is found to be 4.0J/s. If the ends are maintained at temperature s 200∘C and 210∘C. The rate of heat flow will be
View SolutionA metal rod AB of length 10x has it one end in ice at 0∘C and the other end B in water at 100∘C If a point P on the rod is maintained at 400∘C then it is found that equal amounts of water and ice evaporate and melt per unit time. The latent heat of melting of ice is 80cal/g If the point P is at a distance of λx from the ice end A find the value of λ [neglect any heat loss to the surrounding] .
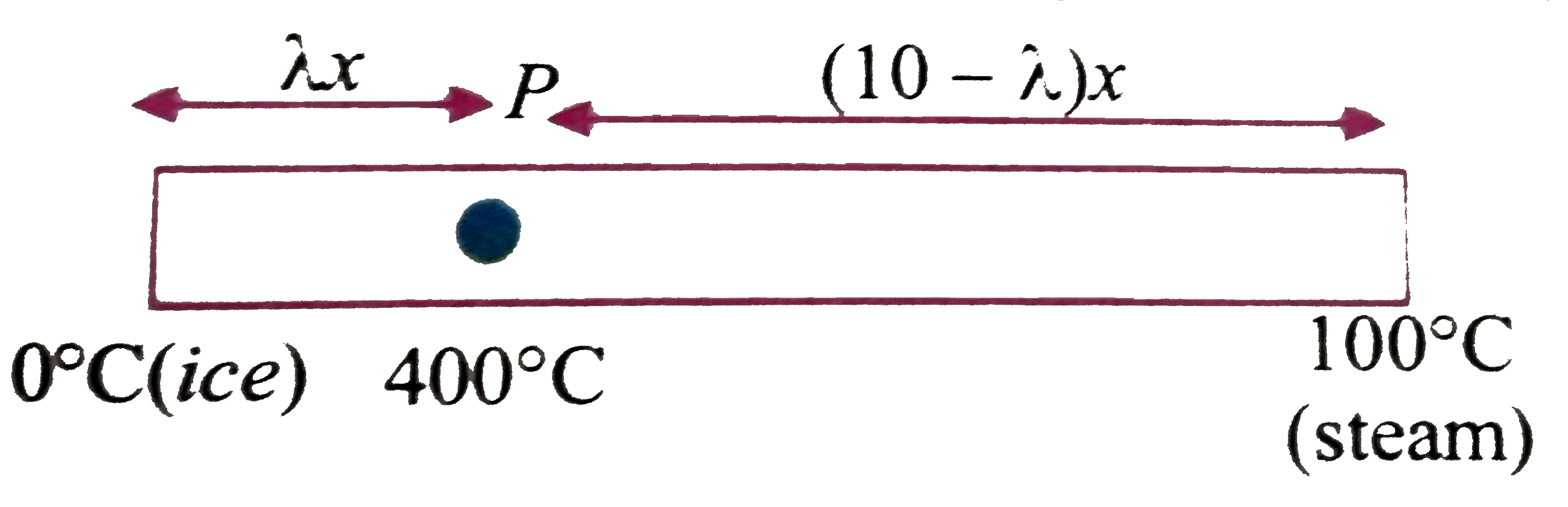 .
.
View SolutionOne end of a brass rod of length 2.0 m and cross section 1cm2 is kept in steam at 100∘C and the other end in ice at 0∘C. The lateral surface of the rod is covered by heat insulator. Determine the amount of ice melting per minute. Thermal conductivity of brass is 110W/m−K and specific latent heat of fusion of ice is 80cal/g.
View SolutionOne end of a steel rod (K=46Js−1m−1C−1) of length 1.0m is kept in ice at 0∘C and the other end is kept in boiling water at 100∘C . The area of cross section of the rod is 0.04cm2 . Assuming no heat loss to the atmosphere, find the mass of the ice melting per second. Latent heat of fusion of ice =3.36×105Jkg−1 .
View SolutionOne end of a copper rod of length 1 m and area of cross - section 400×(10−4)m2 is maintained at 100∘C. At the other end of the rod ice is kept at 0∘C. Neglecting the loss of heat from the surrounding, find the mass of ice melted in 1h. Given, KCu=401W/m−KandLf=3.35×(105)J/kg.
View SolutionOne end of a metal rod is dipped in boiling water and the other is dipped in melting ice.
View Solution
