Two sheets of thickness d and 3d, are touching each other. The temperature just outside the thinner sheet is T1 and on the side of the thicker sheet is T3. The interface temperature is T2.T1,T2andT3 are in arithmetic progression. The ratio of thermal conductivity of thinner sheet to thicker sheet is .
1:3
3:1
2:3
1:9
The correct Answer is:A
To solve the problem, we need to find the ratio of the thermal conductivity of the thinner sheet to that of the thicker sheet given that the temperatures T1,T2,T3 are in arithmetic progression and the thicknesses of the sheets are d and 3d.
1. Understanding the Problem:
- We have two sheets: one with thickness d (thinner sheet) and another with thickness 3d (thicker sheet).
- The temperatures at the outer surfaces are T1 (thinner sheet), T2 (interface), and T3 (thicker sheet).
- The temperatures T1,T2,T3 are in arithmetic progression.
2. Using the Arithmetic Progression:
- Since T1,T2,T3 are in arithmetic progression, we can express this as:
T1−T2=T2−T3
- Rearranging gives:
T1+T3=2T2(1)
3. Applying the Heat Flow Equation:
- The rate of heat flow ˙Q through the sheets can be expressed as:
˙Q=T1−T2R1=T2−T3R2
- Where R1 and R2 are the thermal resistances of the thinner and thicker sheets, respectively.
4. Calculating Thermal Resistance:
- The thermal resistance R for a sheet is given by:
R=LKA
- For the thinner sheet (thickness d):
R1=dK1A
- For the thicker sheet (thickness 3d):
R2=3dK2A
5. Setting Up the Heat Flow Equations:
- Substituting the resistances into the heat flow equations gives:
˙Q=T1−T2dK1A=K1A(T1−T2)d
˙Q=T2−T33dK2A=K2A(T2−T3)3d
6. Equating the Two Expressions for Heat Flow:
- Since ˙Q is constant, we can set the two expressions equal to each other:
K1(T1−T2)d=K2(T2−T3)3d
- Canceling d from both sides gives:
K1(T1−T2)=K2(T2−T3)3
7. Substituting from Equation (1):
- From equation (1), we know T1−T2=T2−T3. Let T1−T2=x, then T2−T3=x.
- Substitute x into the equation:
K1x=K2x3
- Dividing both sides by x (assuming x≠0):
K1=K23
8. Finding the Ratio:
- Rearranging gives:
K1K2=13
- Thus, the ratio of thermal conductivity of the thinner sheet to the thicker sheet is:
K1:K2=1:3
Final Answer:
The ratio of thermal conductivity of the thinner sheet to the thicker sheet is 1:3.
- We have two sheets: one with thickness d (thinner sheet) and another with thickness 3d (thicker sheet).
- The temperatures at the outer surfaces are T1 (thinner sheet), T2 (interface), and T3 (thicker sheet).
- The temperatures T1,T2,T3 are in arithmetic progression.
- Since T1,T2,T3 are in arithmetic progression, we can express this as:
T1−T2=T2−T3
- Rearranging gives:
T1+T3=2T2(1)
- The rate of heat flow ˙Q through the sheets can be expressed as:
˙Q=T1−T2R1=T2−T3R2
- Where R1 and R2 are the thermal resistances of the thinner and thicker sheets, respectively.
- The thermal resistance R for a sheet is given by:
R=LKA
- For the thinner sheet (thickness d):
R1=dK1A
- For the thicker sheet (thickness 3d):
R2=3dK2A
- Substituting the resistances into the heat flow equations gives:
˙Q=T1−T2dK1A=K1A(T1−T2)d
˙Q=T2−T33dK2A=K2A(T2−T3)3d
- Since ˙Q is constant, we can set the two expressions equal to each other:
K1(T1−T2)d=K2(T2−T3)3d
- Canceling d from both sides gives:
K1(T1−T2)=K2(T2−T3)3
- From equation (1), we know T1−T2=T2−T3. Let T1−T2=x, then T2−T3=x.
- Substitute x into the equation:
K1x=K2x3
- Dividing both sides by x (assuming x≠0):
K1=K23
- Rearranging gives:
K1K2=13
- Thus, the ratio of thermal conductivity of the thinner sheet to the thicker sheet is:
K1:K2=1:3
The ratio of thermal conductivity of the thinner sheet to the thicker sheet is 1:3.
Topper's Solved these Questions
Similar Questions
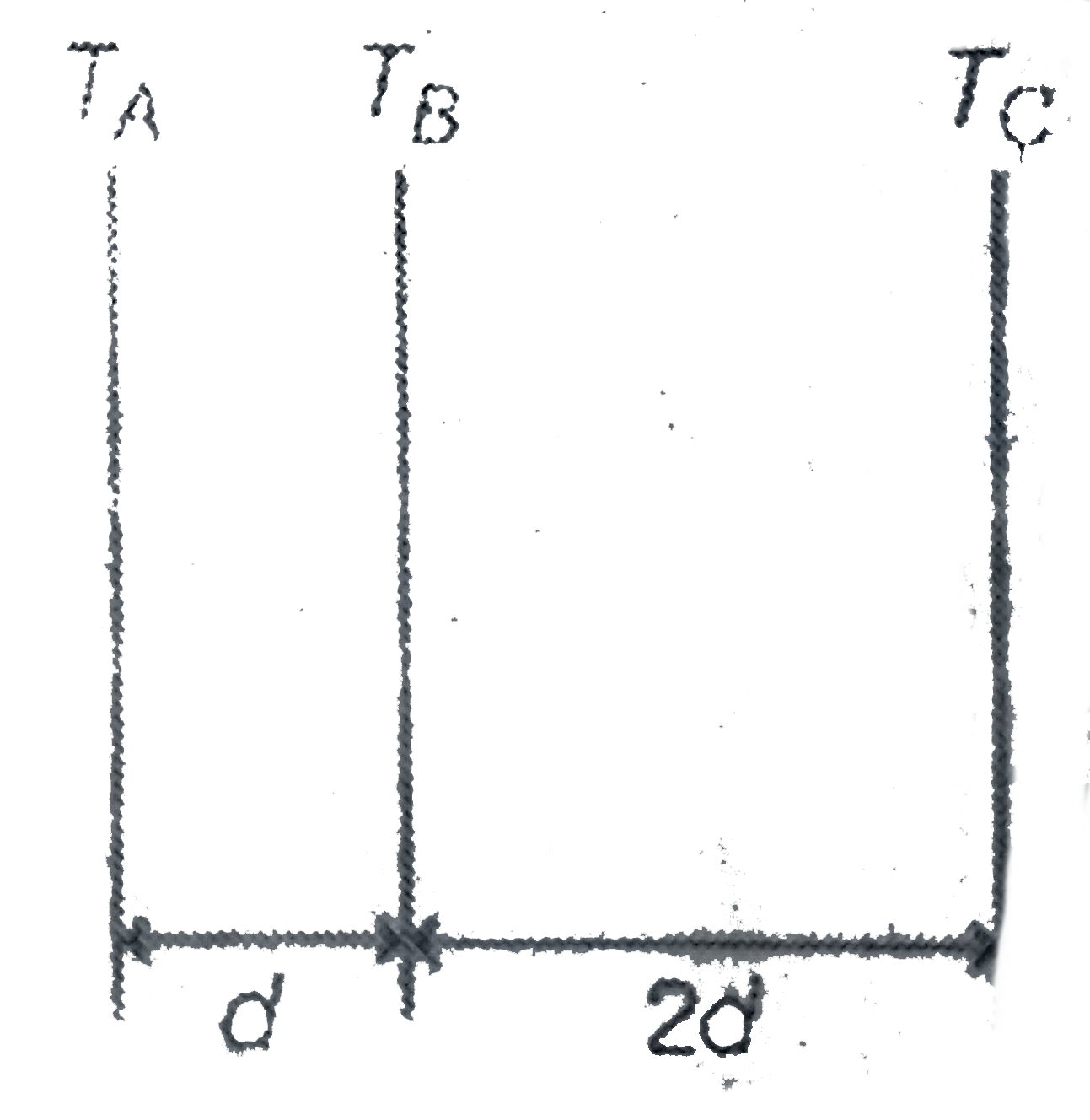
Two sheets of thickness d and 2d and same area are touching each other on their face. Temperature TA,TB,TC shown are in geometric progression with common ratio r = 2. Then ratio of thermal conductivity of thinner and thicker sheet are
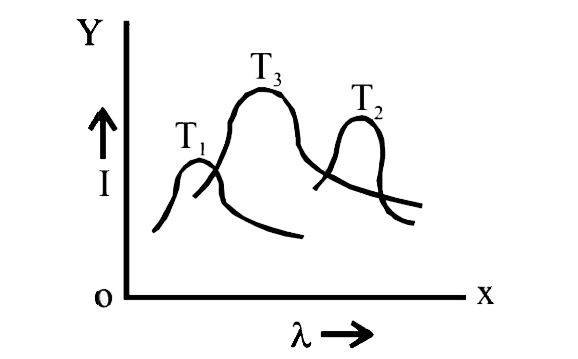
View SolutionThe plots of intensity versus wavelength for three black bodies at temperature T1,T2andT3 respectively are as shown. Their temperatures are such that
View Solution
Knowledge Check
The isothermal diagram of a gas at three different temperatures T1,T2andT3, is show in the given figure .Then
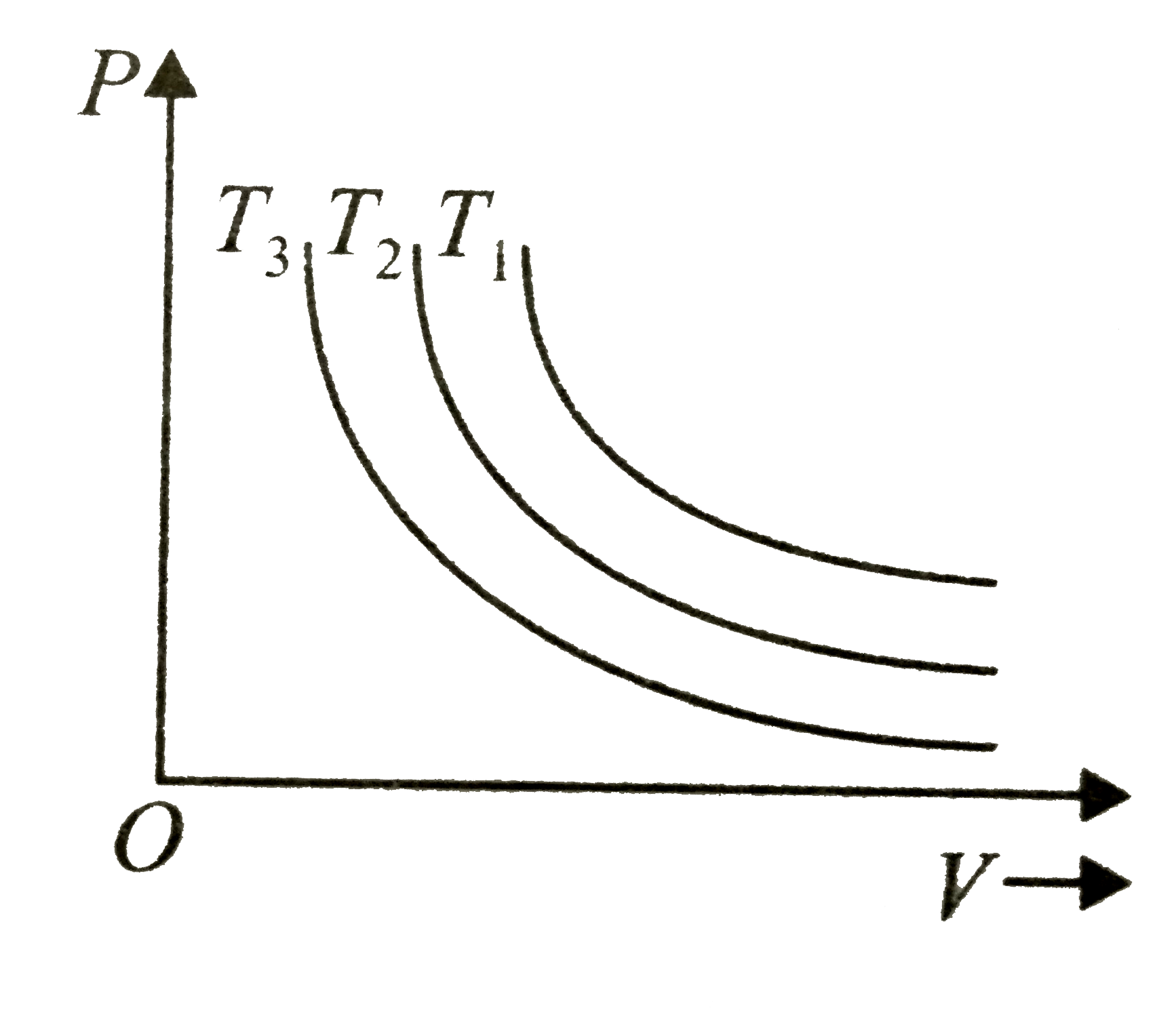 Aa.T1<T2<TBb. T1<T2>T3Cc.T1>T2>T3Dd.T1>T2<T3
Aa.T1<T2<TBb. T1<T2>T3Cc.T1>T2>T3Dd.T1>T2<T3
Find the indicated terms in each of the following arithmetic progression a=3,d=2,tn,t10
View Solution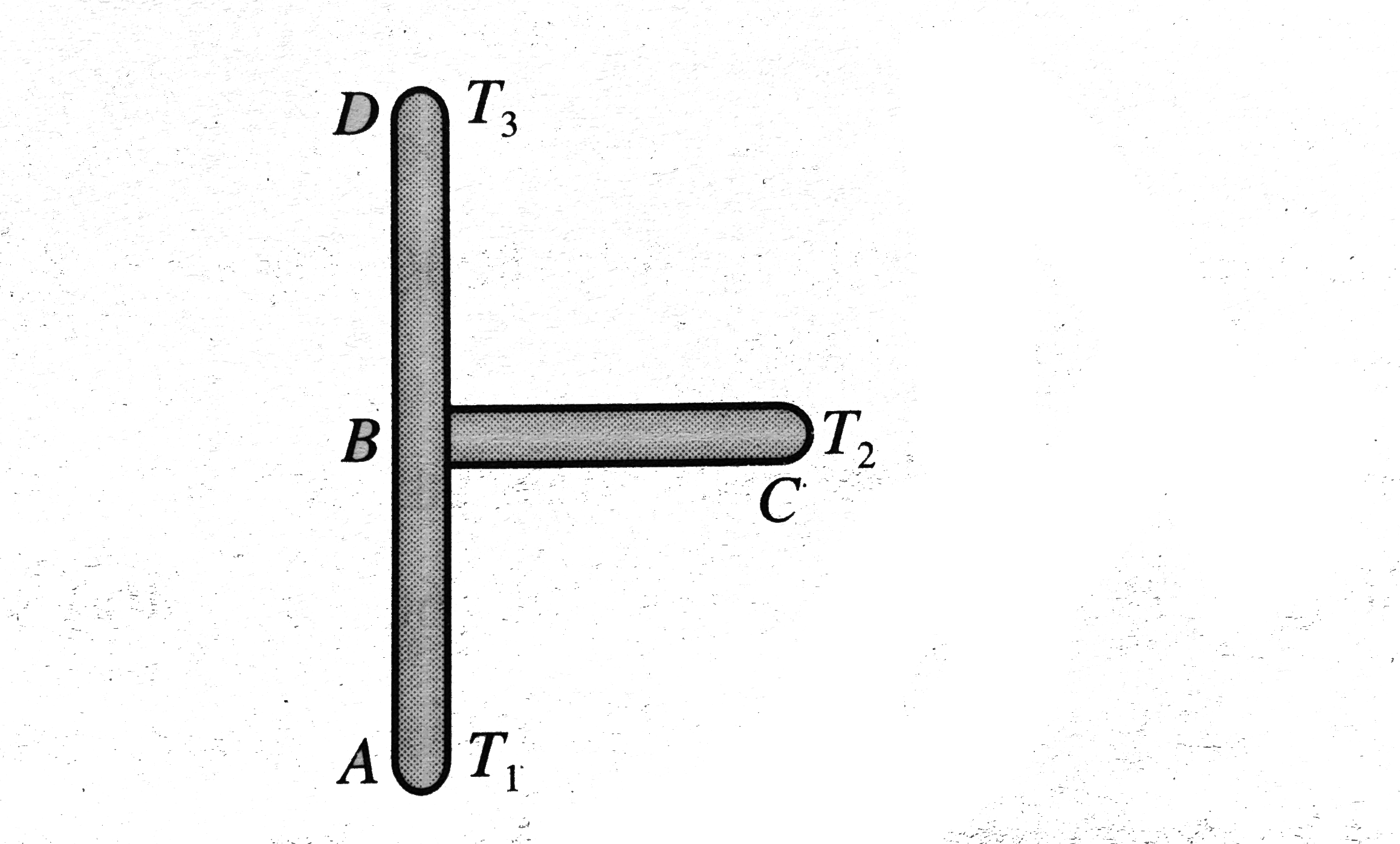
Three rods AB, BC and BD having thermal conductivities in the ratio 1:2:3 and lengths in the ratio 2:1:1 are joined as shown in Fig. The ends A, C and D are at temperature T1,T2 and T3 respectively Find the temperature of the junction B. Assume steady state.
View SolutionTwo bodies of different temperatures T1andT2 if brought in thermal contact, do not necessarily settle to the mean temperature (T1+T2)/2. Why?
View SolutionConsider the two insulating sheets with thermal resistance R1 and R2 as shown in figure. The temperature θ is

View SolutionThe current - voltage graphs for a given metallic wire at two different temperatures T1andT2 are shown in the figure.
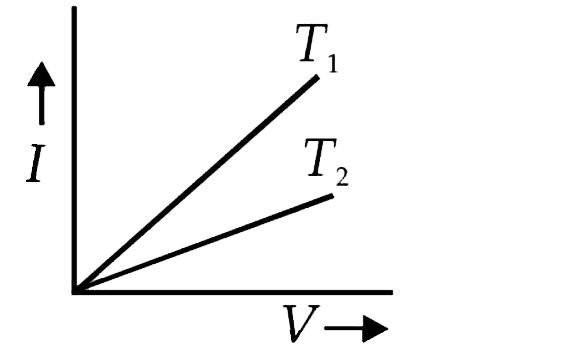
The temperature T2 is greater than T1.
View SolutionThe current - voltage graphs for a given metallic wire at two different temperatures T1andT2 are shown in the figure.

The temperature T2 is greater than T1.
View SolutionA clear sheet of polaroid is placed on the top of similar sheet so that their axes make an angle sin−1(35) with each other. The ratio of intensity of the emergent light to that of unpolarised incident light is
View Solution
