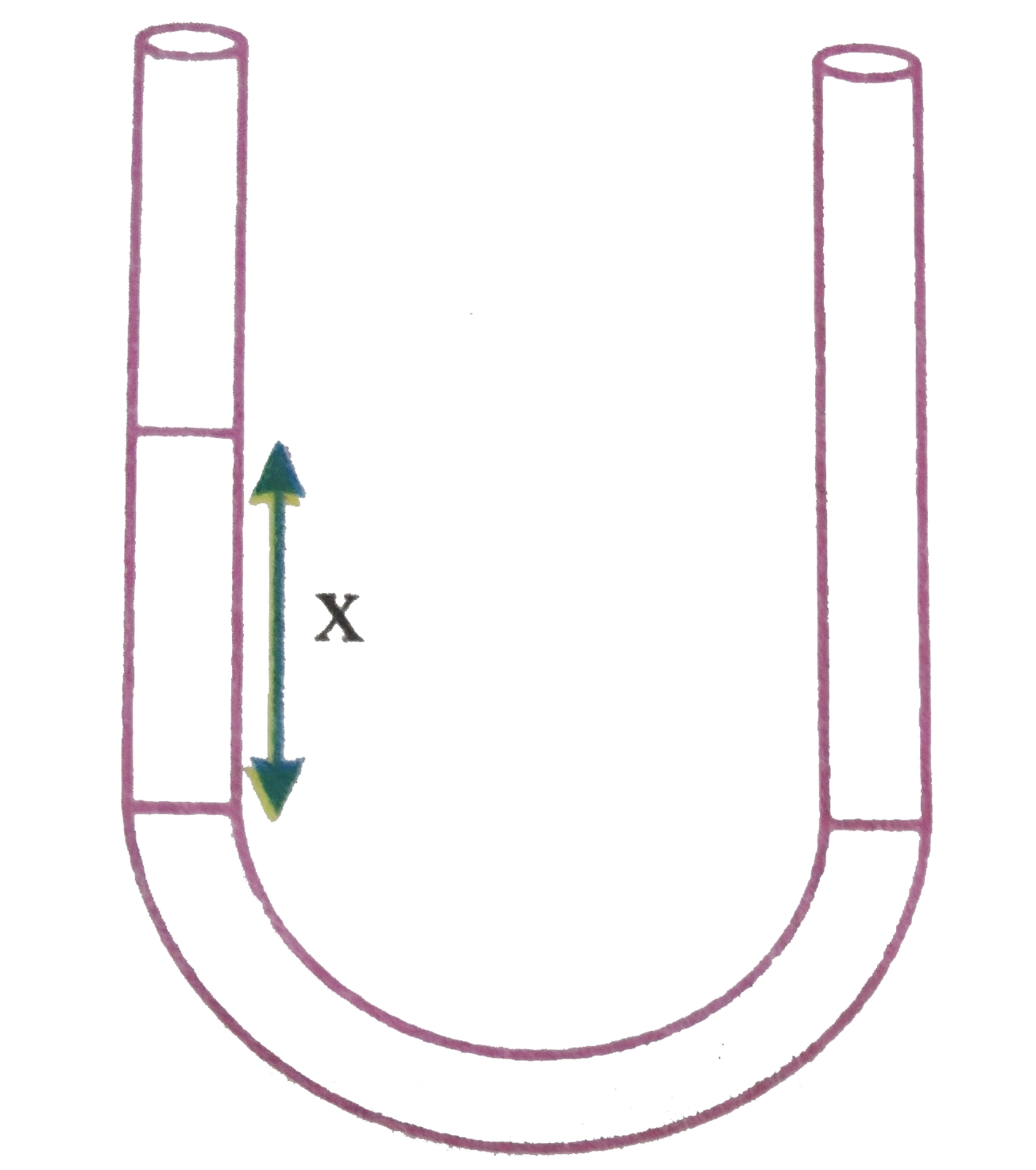
One end of U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
The restoring force,
F = - weight of mercury column at height 2y
= -(volume) × density × g
= −(A×2y×ρ×g)=−2Aρgy
where A = area of cross-section of the tube, ρ = density of mercury.
Force constant, k=−Fy=2Aρ⋅g
So, time period T=2π√mk=2π√m2Aρg
Let L = length of the whole mercury column.
Therefore, mass of mercury,
m = volume × density = ALρ
∴ T=2π√ALρ2Aρg=2π√L2g
where L is the total length of mercury column = 2h, h is the height of mercury column in U-tube. It shows that mercury column executes SHM.
Topper's Solved these Questions
Similar Questions
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View Solution
Knowledge Check
one end of a U-tube of uniform bore (area A) containing mercury is connected to a suction pump. Because of it the level of liquid of density ρ falls in one limb. When the pump is removed, the restoring force in the other limb is:
A2xρAgBxρgCAρgDxρAgOne end a U-tube of unifrom bore (area A) cpmtaining mercury is connected to sunction pump . Because of it the level of liquid of density ρ falls in one limb. When the pump is removed, the restoring force in the other limb is
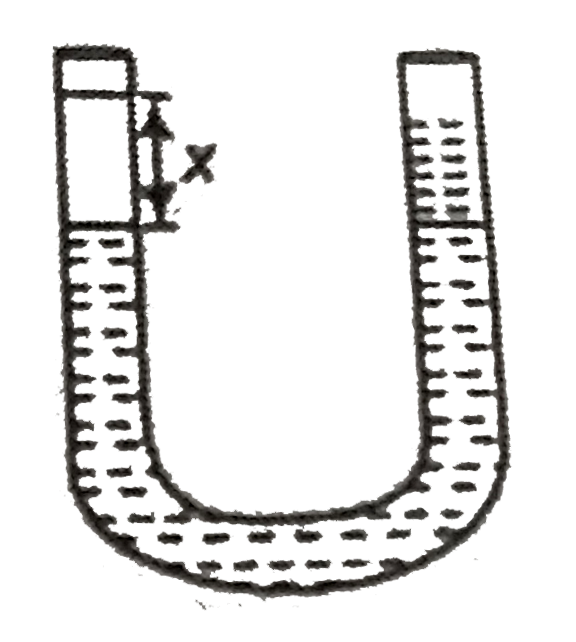 A2xρAgBxρgCAρgDxρAg
A2xρAgBxρgCAρgDxρAgWhat will be the length of mercury column in a barometer tube when the atmospheric pressure is x cm of mercury and the tube is inclined at an angle ϕ with the vertical direction ?
AxsinϕBxcosϕCxtanϕDx
One end of a U-tube containing mercury is connected to a suction pump and the other end to atmosphere. A small pressure difference is maintained between the two columns. Show that, when the suction pump is removed, the column of mercury in the U-tube executes simple harmonic motion.
View SolutionOne end of a U-tube containing mercury is connected to a suction pump and the other end is connected to the atmosphere. A small pressure difference is maintained between the two columns. Show that when the suction pump is removed, the liquid in the U-tube executes SHM.
View SolutionOne end of V-tube containing mercury is connected to a suction grouup and the other end to atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45∘ each. A small pressure difference is created between two columns when the ssuction pump is removed. Will the column of mercuty in V-tube execute simple harmonic motion? Neglect capillary and viscous forces. Fing the time period of oscillation.
View SolutionOne end of a V-tube containing mercury is connected ot a suction pump and the other end to atmosphere. The two arms of the tube are inclined to horizontal at an angle of 45∘ each. A small pressure difference is created between two columns when the suction pump is removed. Will Neglect capillary and viscous forces. Find the time period of oscillation.
View SolutionAn ideal gas is trapped between a mercury column and the closed lower end of a narrow vertical tube of uniform bore. The upper end of the tube is open to atmosphere (atmospheric pressure = 76 cm of Hg). The length of mercury and the trapped gas columns are 20 cm and 43 cm respectively. What will be the length of the gas column when the tube is titled slowly at constant temperature in a vertical plane through an angle of 60∘ ?
View Solution
