One mole of a monoatomic ideal gas is taken through the cycle shown in Fig:
A→B: adiabatic expansion
B→C: cooling at constant volume
C→D: adiabatic compression
D→A: heating at constant volume
![One mole of a monoatomic ideal gas is taken through the cycle shown in Fig: AtoB: adiabatic expansion BtoC: cooling at constant volume CtoD: adiabatic compression DtoA: heating at constant volume The pressure and temperature at A,B,etc. are denoted by PA, TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2//3)PA and PC=(1//3)PA, calculate the following quantities: (i) The work done by the gas in the process AtoB (ii) The heat lost by the gas in the process BtoC. (iii) The temperature TD. [Given :(2//3)^(2//5)=0.85]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/JMA_HTG_C09_118_Q01.png)
The pressure and temperature at A,B,etc. are denoted by PA,TA,PB,TBetc. respectively. Given that TA=1000K, PB=(2/3)PAandPC=(1/3)PA, calculate the following quantities:
(i) The work done by the gas in the process A→B
(ii) The heat lost by the gas in the process B→C.
(iii) The temperature TD. [Given :(2/3)2/5=0.85]
a. The work done in adiabatic process AB is given by
W1R(TA−TB)γ−1=R(TA−TB)(5/3)−1
(as for monatomic gas γ=5/3)
or =32R(TA−TB)
For adiabatic change, we have
Pγ−1ATγA=Pγ−1BT−γB
or (PAPB)=(TATB) or (IAIB)=(PAPB)2/5
or (TATB)=(32)2/3
or TB=TA(23)2/3
=1000×0.85=850K
From Eq. (i)
W1=32×8.31×(1000−850)=1869.83J
b. Heat lost by the gas in process BC is given by
CV(TB−TC)=(Rγ−1)(TB−TC)=(32)R(TB−TC)
Process BC is under constant volume , hence
(PBTB)=(PCTC) or TC=(PCPB)×TB
or TC=(PA/3)2PA/3TB=(T2)=425K
From Eq. (ii) we get
Heat lost =(32)×8.31×(850−425)=5279.63J
c. For path AB
Pγ−1AT−γA=Pγ−1BT−γB
or (PAPB)γ−1=(TATB)γ
For path BC
(PBTB)=(PCTC) or (PBPC)=(TBTC)
For path CD
(PDTB)γ−1=(TDTC)γ
Fro path AD
(PAPD)=(TATC)
Dividing Eq. (viii) by Eq. (vii), we get
(PAPB×PCPD)γ−1 = (TATB×TCTD)γ
Dividing Eq. (viii) by Eq. (iv) we get
(PAPB×PCPD) = (TATB×TCTD) or (PAPB×PCPD)γ−1=(TATB×TCTD)γ−1
(TATB×TCTD)γ=(TATB×TCTD)γ−1
TATC=TDTB
1000×425=TD×850
TD=500K
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.1
20 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Exercise 2.2
28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
Similar Questions
One mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion

B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The work done by the gas in process A→B (in J)
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
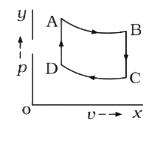
B→C: cooling at constant volume
C→D adiabatic compression D→C: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(t/3)PA
Calculate the following quantities.
The heat lost by the gas in process B→C (in J)
View Solution
Knowledge Check
One mole of a monatomic ideal gas is taken through the cycle shown in figure
 The pressures and temperatures at A,B etc, are denoted by PA,TA,PB,TBetc respectively.Given TA=1000K,PB=(2/3)PAandPC=(1/3)PA Then choose the incorrect option. AThe work done by the gas in the process A→B is 1869.75JBThe heat lost by the gas sin the process B→C is -5297.25JCTemperature TD is 500KDWork done from B→C is 40J
The pressures and temperatures at A,B etc, are denoted by PA,TA,PB,TBetc respectively.Given TA=1000K,PB=(2/3)PAandPC=(1/3)PA Then choose the incorrect option. AThe work done by the gas in the process A→B is 1869.75JBThe heat lost by the gas sin the process B→C is -5297.25JCTemperature TD is 500KDWork done from B→C is 40JOne mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC

[Assume(23)0.4=0.85 and R=253JK−1mol−1]
The temperature at B isA350KB1175KC850KD577KOne mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
ARΔTB3RΔTC5RΔTD6RΔT
On mole of a monoatomic ideal gas is taken through the cycle shown in figure .
A→B : Adiabatic expansion B→C : Cooling at constant volume
C→D: Adiabatic compression D→A : Heating at constant volume
The pressure and temperature at A,B, etc, are denoted by PA,TA,PB,TB etc., respectively . Given that TA=1000K,PB=(23)PAandPC=(13)PA. Calculate the following quantities: (i) The work done by the gas in the processs A→B (ii) The heat lost by the gas in the process B→C (iii) The temperature TD.(Given:(23)2/5=0.85)
_E01_271_Q01.png)
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in figure.
A→B Adiabatic expansion
B→C Cooling at constant volume
C→D Adiabatic compression.
D→A Heating at constant volume
The pressure and temperature at A,B etc., are denoted by pA,TA,pB,TB etc. respectively.
Given, TA=1000K, pB=(23)pA and pC=(13)pA. Calculate
(a) the work done by the gas in the process A→B
(b) the heat lost by the gas in the process B→C
Given, (23)0.4=0.85 and R=8.31J/mol−K
View SolutionOne mole of a monatomic ideal gas is taken through the cycle shown in the figure: A→B adiabatic expansion
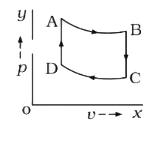
B→C: cooling at constant volume
C→D adiabatic compression D→A: heating at constant volume.
The pressure and temperature at PA,PB etc. TA,TB etc. are denoted etc. respectively. Given that
TA=1000K,PB=(2/3)PA and PC=(1/3)PA
Calculate the following quantities.
The temperature TD (in K) [Given : (25)2/5=0.85 ]
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC

[Assume(23)0.4=0.85 and R=253JK−1mol−1]
Heat lost by the gas in the process B→C is
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle ABCDA as shown in the figure.
TA=1000K and 2pA=3pB=6pC

[Assume(23)0.4=0.85 and R=253JK−1mol−1]
Work done by the gas in the process A→B is
View Solution
