Particle A of mass moving along the x - axis with velocity collides elastically with another particle B at rest having mass . If both particles move along the x - axis after the collision , the change in de - Broglie wavelength of particle A , in terms of its de - Broglie wavelength before collision is :
To solve the problem, we need to analyze the elastic collision between two particles, A and B, and find the change in the de Broglie wavelength of particle A after the collision.
1. Identify the Masses and Initial Velocities:
- Mass of particle A, mA=m2
- Mass of particle B, mB=m3
- Initial velocity of particle A, v0
- Initial velocity of particle B, vB=0 (since it is at rest)
2. Conservation of Momentum:
The total momentum before the collision must equal the total momentum after the collision.
mAv0+mBvB=mAv1+mBv2
Substituting the values:
m2v0+0=m2v1+m3v2
Simplifying this gives:
m2v0=m2v1+m3v2
Dividing through by m (assuming m≠0):
12v0=12v1+13v2(Equation 1)
3. Conservation of Kinetic Energy:
Since the collision is elastic, the kinetic energy before and after the collision is conserved:
12mAv20+0=12mAv21+12mBv22
Substituting the masses:
12⋅m2v20=12⋅m2v21+12⋅m3v22
Dividing through by 12m:
12v20=12v21+13v22(Equation 2)
4. Solving the Equations:
From Equation 1, we can express v1 in terms of v2:
v1=v0−32v2
Substituting this expression for v1 into Equation 2:
12v20=12(v0−32v2)2+13v22
Expanding and simplifying will yield values for v1 and v2.
5. Finding Final Velocity of Particle A:
After solving the equations, we find the final velocity v1 of particle A. For example, let's say we find:
v1=15v0
6. Calculating the de Broglie Wavelength:
The de Broglie wavelength is given by:
λ=hmv
Before the collision, the de Broglie wavelength of particle A is:
λ0=hmAv0=hm2v0=2hmv0
After the collision, the de Broglie wavelength of particle A becomes:
λ1=hmAv1=hm2⋅15v0=10hmv0
7. Change in de Broglie Wavelength:
The change in de Broglie wavelength is:
Δλ=λ1−λ0=10hmv0−2hmv0=8hmv0
In terms of λ0:
Δλ=4λ0
Final Answer:
The change in the de Broglie wavelength of particle A, in terms of its de Broglie wavelength before the collision, is:
Δλ=4λ0
- Mass of particle A, mA=m2
- Mass of particle B, mB=m3
- Initial velocity of particle A, v0
- Initial velocity of particle B, vB=0 (since it is at rest)
The total momentum before the collision must equal the total momentum after the collision.
mAv0+mBvB=mAv1+mBv2
Substituting the values:
m2v0+0=m2v1+m3v2
Simplifying this gives:
m2v0=m2v1+m3v2
Dividing through by m (assuming m≠0):
12v0=12v1+13v2(Equation 1)
Since the collision is elastic, the kinetic energy before and after the collision is conserved:
12mAv20+0=12mAv21+12mBv22
Substituting the masses:
12⋅m2v20=12⋅m2v21+12⋅m3v22
Dividing through by 12m:
12v20=12v21+13v22(Equation 2)
From Equation 1, we can express v1 in terms of v2:
v1=v0−32v2
Substituting this expression for v1 into Equation 2:
12v20=12(v0−32v2)2+13v22
Expanding and simplifying will yield values for v1 and v2.
After solving the equations, we find the final velocity v1 of particle A. For example, let's say we find:
v1=15v0
The de Broglie wavelength is given by:
λ=hmv
Before the collision, the de Broglie wavelength of particle A is:
λ0=hmAv0=hm2v0=2hmv0
After the collision, the de Broglie wavelength of particle A becomes:
λ1=hmAv1=hm2⋅15v0=10hmv0
The change in de Broglie wavelength is:
Δλ=λ1−λ0=10hmv0−2hmv0=8hmv0
In terms of λ0:
Δλ=4λ0
The change in the de Broglie wavelength of particle A, in terms of its de Broglie wavelength before the collision, is:
Δλ=4λ0
Topper's Solved these Questions
Similar Questions
A particle of mass m1 moves with velocity v1 and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is
View SolutionA particle of mass m moving with velocity u collides elastically head on with a particle of mass 2m at rest. After collision the heavier particle moves with velocity?
View Solution
Knowledge Check
A particle of mass m moving with speed V collides eleastically with another particle of mass 2mFind speed of smaller mass after head on collision
Av3B−v3C2v3D−2v3If a ball A of mass mA=m2 moving along x-axis collides elastically with ball B of mass mB=m3 initially at rest and they move along x-axis. If initially velocity of ball A was v0. And initially de-broglie wavelength of ball A is λ0. Find change in debroglie wavelength δλ of ball A in terms of λ0
A3/2 λ0B5/3 λ0C4 λ0D3 λ0A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
A34μ2B38μ2C14μ2D18μ2
A body of mass m moving with velocity v collides head-on elastically with another body of mass 2m which is initially at rest. The ratio of K. E. of mass m before and after the collision will be
View SolutionA particle of mass m is moving along the x-axis with initial velocity u i . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
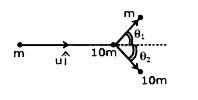
View SolutionWrite the relationship of de-Broglie wavelength λ associated with a particle of mass m in terms of its kinetic energy.
View SolutionA particle of mass m moving eastward with a speed v collides with another particle of the same mass moving coalesce on collision. The new particle of mass 2m will move in the north - easterly direction with a velocity
View SolutionThe de-Broglie wavelength of a particle with mass 1g and velocity 100m/sec is.
View Solution
