Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
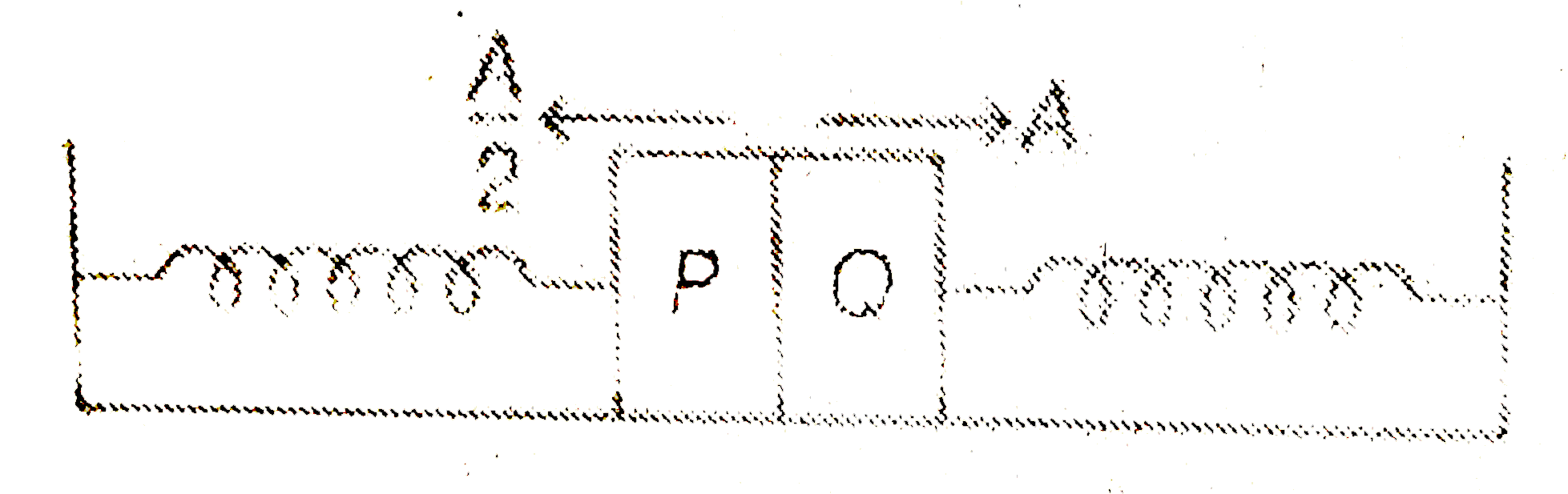
The time period of oscillation of combined mass is
T√2
√T
T
T2
The correct Answer is:C
Step by step video, text & image solution for Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A/2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T. The time period of oscillation of combined mass is by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions

The period of oscillation of a mass M suspended from a spring of spring constant K is T. the time period of oscillation of combined blocks is
View Solution(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.

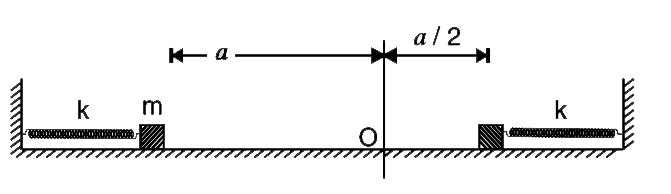
View Solution
Knowledge Check
Two identical blocks P and Q have mass m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A/2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both the blocks was T.
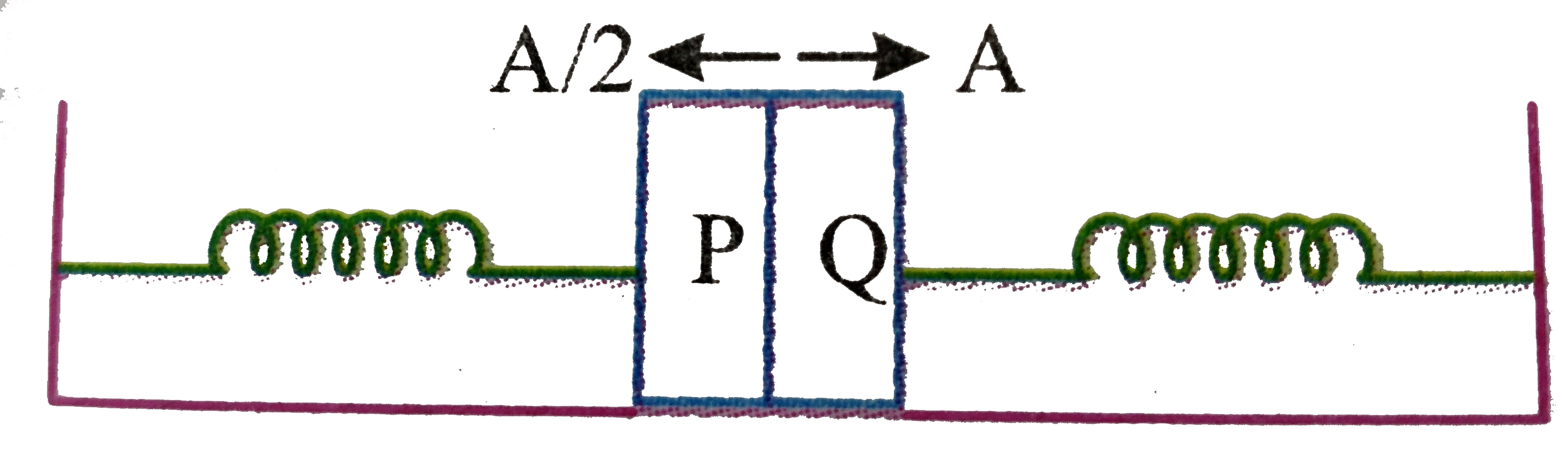
The time period of oscillation of combined mass isAT√2B√2TCTDT2Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
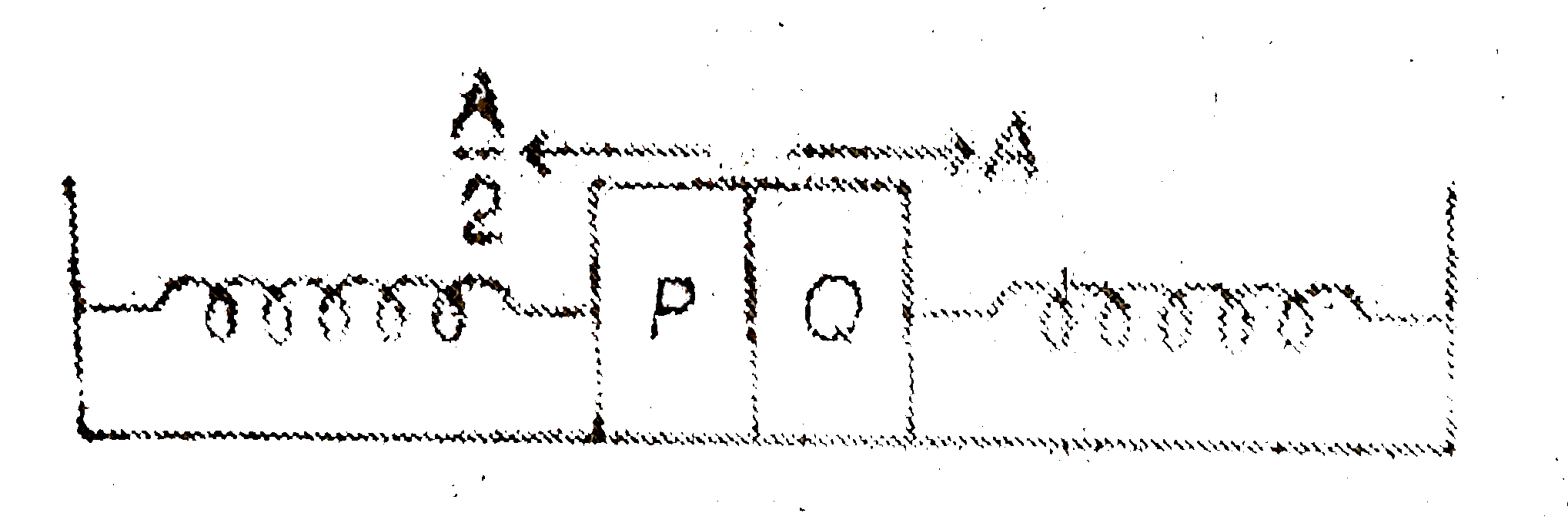
What is energy of osciallation of the combined mass?A12kA2B14kA2C18kA2D(116)kA2Passage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
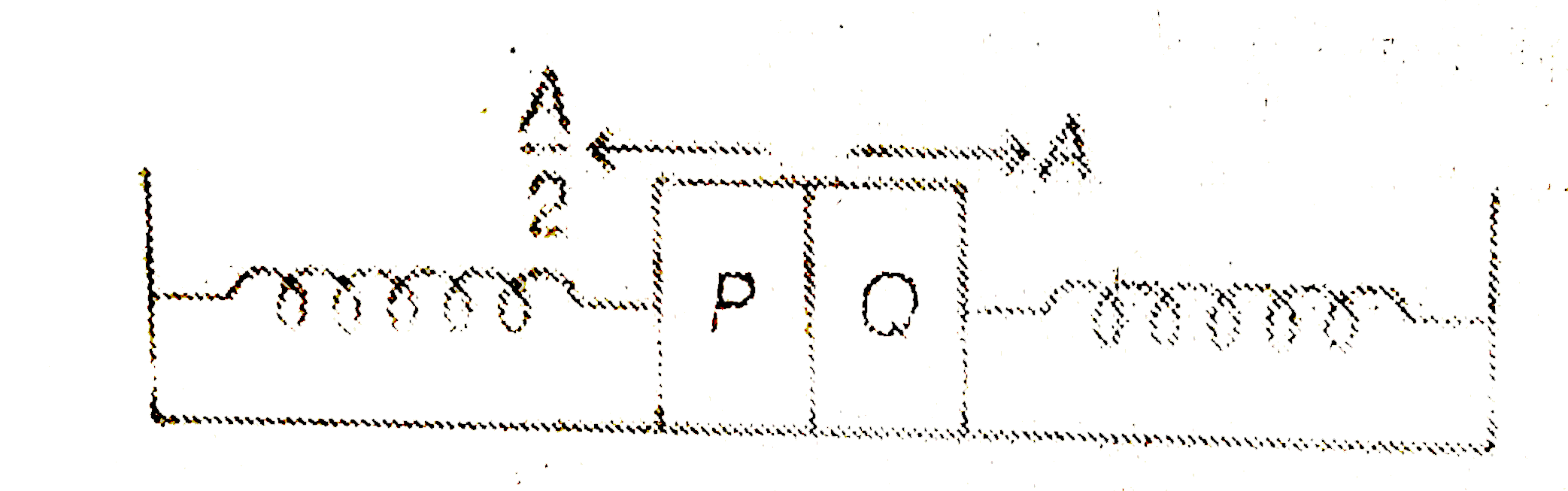
The amplitude of combined mass isAA4BA2C2A3D3A4
Two identical blocks P and Q have mass m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A/2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both the blocks was T.
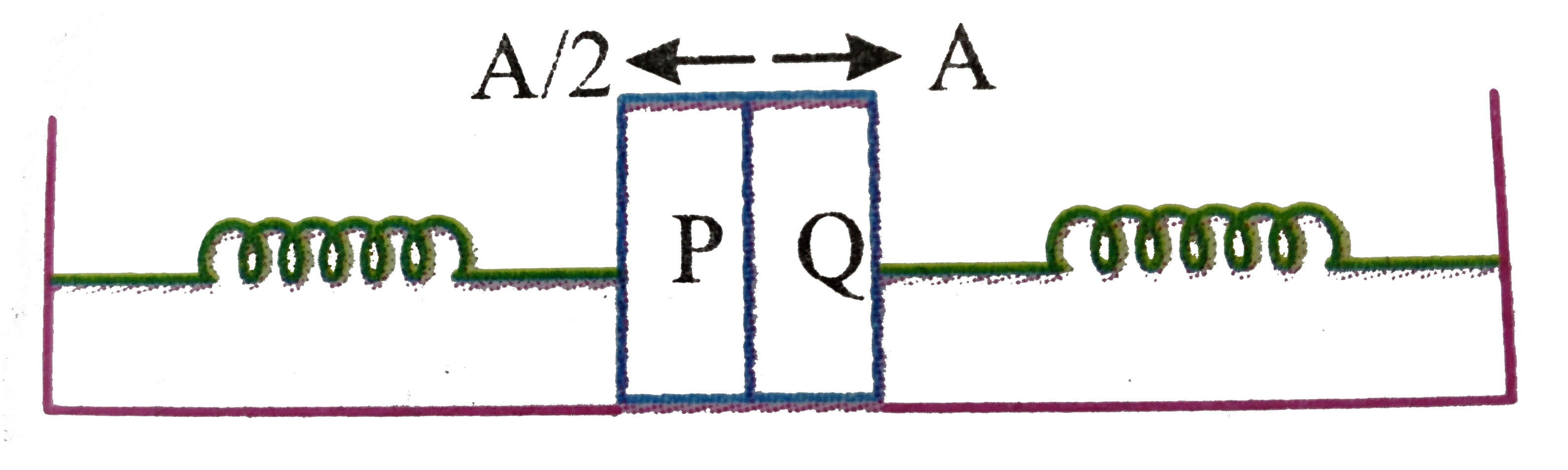
The energy of oscillation of the combined mass is
View SolutionPassage II) Two identicla blocks P and Q have masses m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by A2 and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both blocks was T.
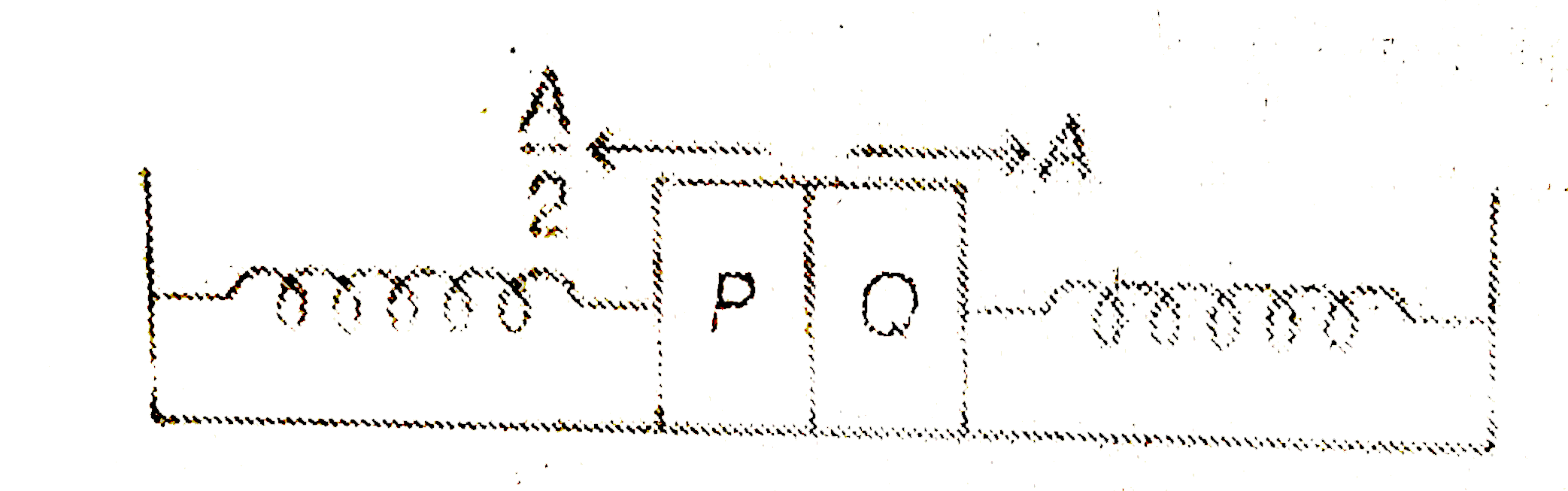
The amplitude of combined mass is
View SolutionTwo identical blocks P and Q have mass m each. They are attached to two identical springs initially unstretched. Now the left spring (along with P) is compressed by (A/2) and the right spring (along with Q) is compressed by A. Both the blocks are released simultaneously. They collide perfectly inelastically. Initially time period of both the block (assuming each block was individually connected to one spring) was T.
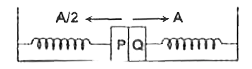
The amplitude of combined mass is
View SolutionA block of mass 'm' collides perfectly inelastically with another identical block connected to a spring of of force constant 'K'. The amplitude of resulting SHM will be
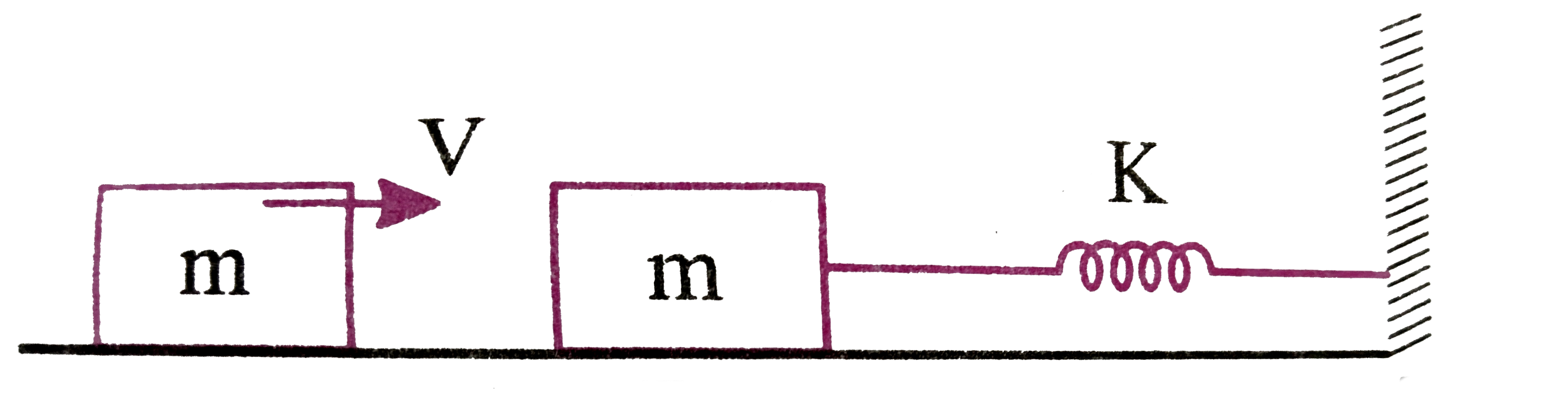
View Solution
Two blocks of mass M and m, are used to compress two different massless spring as shown. The left spring is compressed by 3 cm, while the right spring is compressed by an unknown amount.. The system is at rest, and all surfaces fixed and smooth. Which of the following statements are true?
View Solution
