(i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other.
(a) If the small displacement of blocks is x then find the magnitude of acceleration of m2. What is time period of oscillations ?
(b) Find the ratio m1m2 so that the frictional force on m2 acts in the direction of its displacement from the mean position.
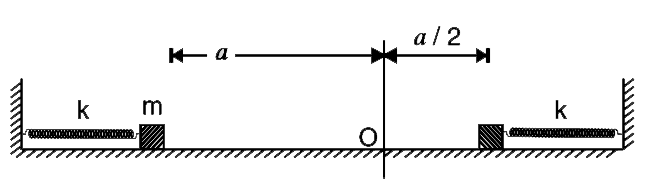
(ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a/2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks)
(a) Collisions between them are elastic.
(b) Collisions between them are perfectly inelastic.
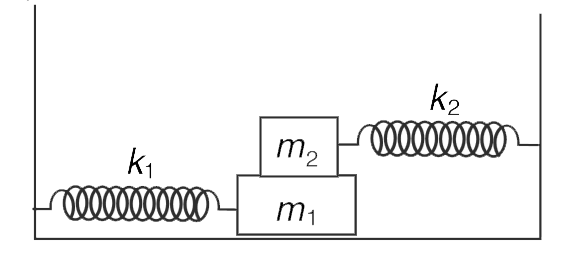
The correct Answer is:(a) a=(k1+k2m1+m2)x;T=2π√m1+m2k1+k2
(b) m1m2>k1k2;T=2π√mk " for both the blocks in both cases".
Step by step video, text & image solution for (i) In the shown arrangement, both springs are relaxed. The coefficient of friction between m_(2) " and " m_(1) is mu. There is no friction between m_(1) and the horizontal surface. The blocks are displaced slightly and released. They move together without slipping on each other. (a) If the small displacement of blocks is x then find the magnitude of acceleration of m_(2). What is time period of oscillations ? (b) Find the ratio (m_(1))/(m_(2)) so that the frictional force on m_(2) acts in the direction of its displacement from the mean position. (ii) Two small blocks of same mass m are connected to two identical springs as shown in fig. Both springs have stiffness K and they are in their natural length when the blocks are at point O. Both the blocks are pushed so that one of the springs get compressed by a distance a and the other by a//2. Both the blocks are released from this position simultaneously. Find the time period of oscillations of the blocks if - (neglect the dimensions of the blocks) (a) Collisions between them are elastic. (b) Collisions between them are perfectly inelastic. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 2
33 Videos
- SIMPLE HARMONIC MOTIONBOOK - ARIHANTCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 3
9 Videos
- ROTATIONAL MOTIONBOOK - ARIHANTCHAPTER - ROTATIONAL MOTIONEXERCISE - PHYSICS
159 Videos
- SURFACE TENSIONBOOK - ARIHANTCHAPTER - SURFACE TENSIONEXERCISE - Surface tension
33 Videos
Similar Questions
Two particles A and B are describing SHM of same amplitude (a) and same frequency (f) along a common straight line. The mean positions of the two SHMs are also same but the particles have a constant phase difference between them. It is observed that during the course of motion the separation between A and B is always less than or equal to a.
(a) Find the phase difference between the particles.
(b) If distance between the two particles is plotted with time, with what frequency will the graph oscillate?
View SolutionTwo particles of mass m1 and m2 are connected by a spring of natural length L and force constant k. The masses are brought close enough so as to compress the spring completely and a string is used to tie the system. Assume that length of spring in this position is close to zero. The system is projected with a velocity V0 along the positive x direction. At the instant it reaches origin at time t = 0, the string snaps and the spring starts opening.
(a) Show that the mass m1(orm2) will are perform SHM in the reference frame attached to the centre of mass of the system. Find the time period of oscillation.
(b) Write the amplitude of m1 and m2 as a function of time. lt( c) Write the X co ordinates of m1 and m2 as a function of time

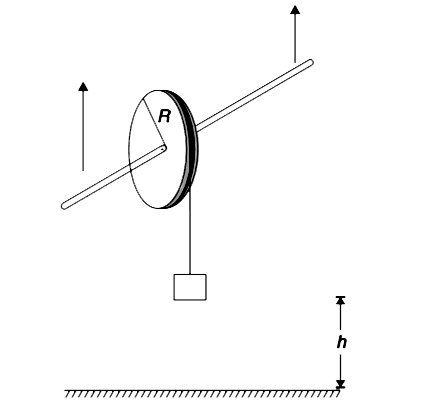
View SolutionThe pulley of radius R can rotate freely about its axle as shown in the figure. A thread is tightly wrapped around the pulley and its free end carries a block of mass m. When the block is at a height h above the ground the system is released (i.e., the pulley is made free to rotate & the block is allowed to fall) and at the same instant the axle is moved up keeping it horizontal all the time. When the block hits the floor the axle has gone up by a distance 2h. Find the angle by which the pulley must have rotated by this time.
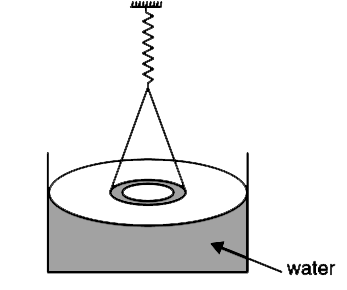
View SolutionA circular ring has inner and outer radii equal to 10mmand30mm respectively Mass of the ring is m=0.7 g. It gently pulled out vertically from a water surface by a sensitive spring. When the spring is stretched 3.4cm from its equilibrium position the ring is on verge of being pulled out from the water surface. If spring constant is k=0.7Nm–1 find the surface tension of water.
View SolutionTwo blocks of masses m_(1) and m_(2) are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between m_(1) and platform is 2mu and that between block m_(2) and platform is mu .The platform moves with an acceleration a . The normal reation between the blocks is
View SolutionIn the shown arrangement, both the spring are in their natural lengths. The coefficient of friction between m2 and m1 is μ. There is no friction between m1 and the surface. If the blocks are displaced slightly, they together perform simple harmonic motion. Obtain

(a) Frequency of such oscillations.
(b) The condition if the friction force on clock m2 is to act in the direction of its displacement from mean position.
( c) If the condition obtained in (b) is met, what can be maximum of their oscillations ?
View SolutionTwo block , with masses m1 and m2 are staked as shown in fig and placed on a frictionless horizontal surface . There is a friction between the two block .An external force of magnitude F is applied to the top block at an angle α below the horizontal . The coefficient of friction between m1 and m2 are μs
b. If the two blocks move together, find their acceleration
b . Calculate the maximum value of force so that blocks will move together

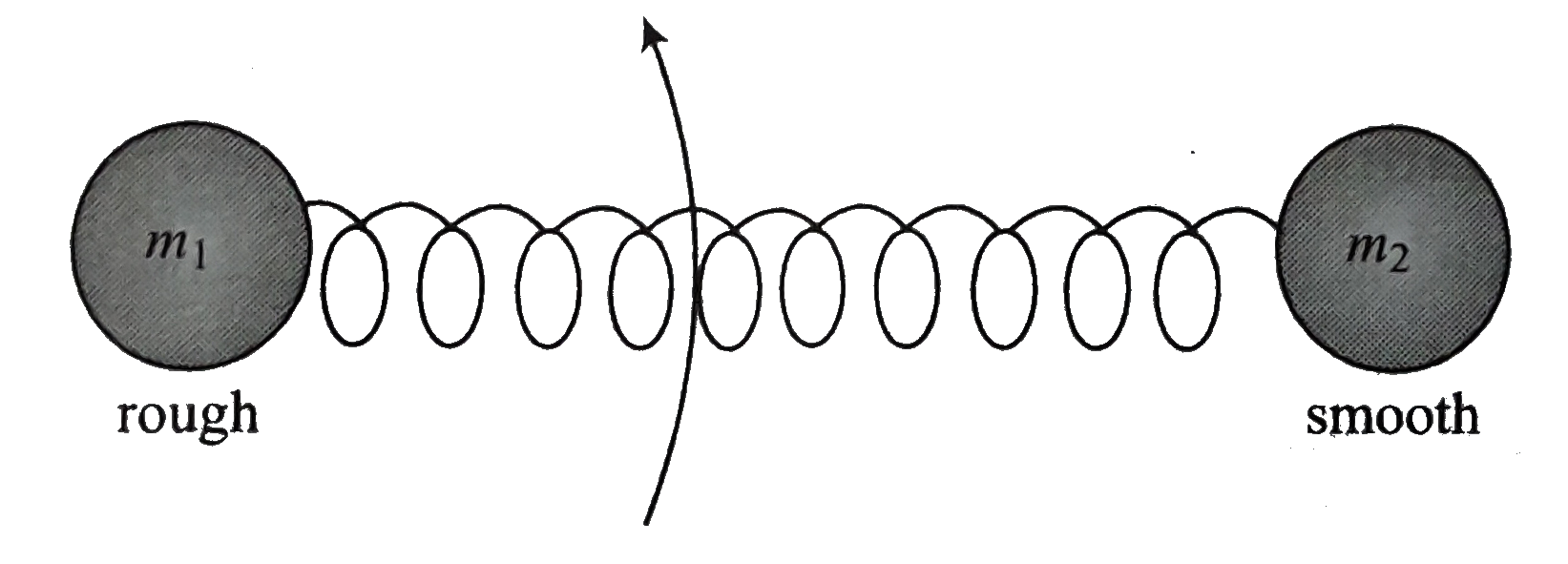
View SolutionA block of mass m1 connected with another of mass m2 by a light spring of natural length l0 and stiiffness k is kept stationary on a rough horizontal surface . The coefficient of friction between m1 and surface is μ and the block m2 is smooth .The block m2 is moved with certain the block m1 in horizontal plane Find the (a) maximum to m1 and (b) acceleration of m2 in part(a)
View SolutionTwo blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform. The coefficient of friction between the platform and the two blocks is the same. The platform moves with an acceleration. The force of interaction between the blocks is :

View SolutionTwo block M_(1) and M_(2) rest upon each other on an inclined plane Coefficient of friction between surfaces are shown if the angle 0 is slowly increased and M_(1) le M_(2) then
View SolutionIn figure-2.86, the blockA of mass M_(1) rests on a rough horizontal surface. The coefficient of friction between the block and the surface is mu . A uniform plank B, of mass M_(2) rests on A. B is prevented from moving by connecting it to a light rod R which is hinged at one end H.The coefficient of friction between A and B is mu . Findthe acceleration of blocks A and C. [(M_(3)g-mug(M_(1)+2M_(2)))/((M_(1)+M_(3)))]
View SolutionTwo blocks of masses m1 and m2 kept touching each other on an inclined plane of inclination a with the horizontal. Show that (i) theforce of interaction between the blocks is (μ1−μ2)m1m2gcosα(m1+m2) and (ii) the minimum value of α at which the blocks just start sliding is a=tan−1.μ1m1+μ2m2m1+m2 . Where μ1 and μ2 are the coefficients of friction between the block m1 and the inclined plane and between the block m2 and the inclinedplane respectively.
View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.



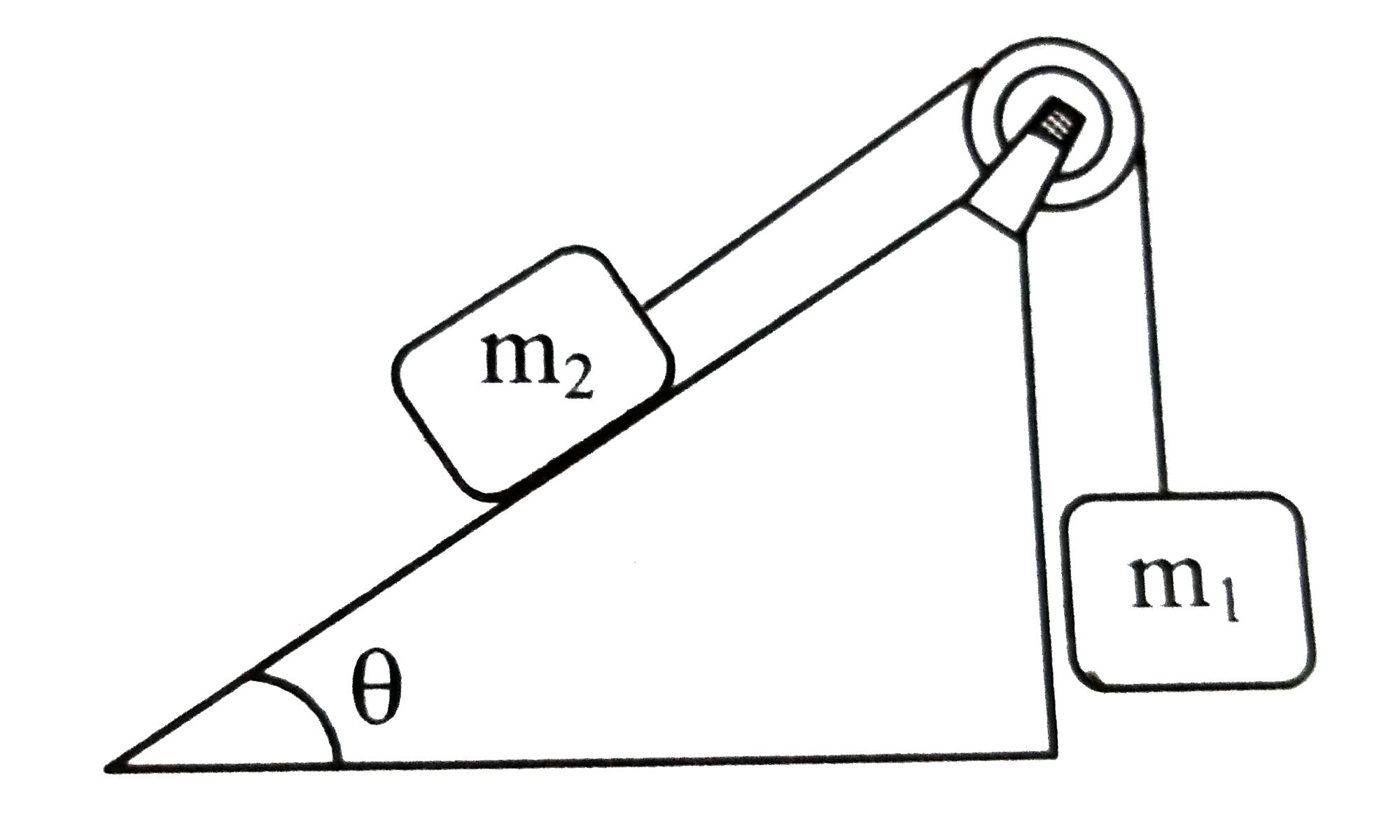
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View Solution
