Passage VI Two particles collide when they are at same position at same time.
Displacement time equation of two particles moving along x-axis are x1=(8+3sinωt)m
and x2=(4cosωt)m
Here, ω=πrads
The two particles will collide after time t=...................s.
1
2
4
None of the above.
The correct Answer is:D
To solve the problem, we need to find the time at which the two particles collide, meaning their displacements x1 and x2 are equal. The displacement equations are given as:
x1=8+3sin(ωt)
x2=4cos(ωt)
where ω=π rad/s.
Step 1: Set the equations equal to each other
To find the time when the two particles collide, we set their displacement equations equal to each other:
8+3sin(πt)=4cos(πt)
Step 2: Rearrange the equation
Rearranging the equation gives us:
3sin(πt)−4cos(πt)+8=0
Step 3: Isolate the trigonometric terms
We can isolate the trigonometric terms:
3sin(πt)=4cos(πt)−8
Step 4: Divide by cos(πt)
To solve for t, we can divide both sides by cos(πt) (assuming cos(πt)≠0):
3tan(πt)=4−8cos(πt)
Step 5: Analyze the ranges of x1 and x2
Now, we need to analyze the ranges of x1 and x2:
- For x1:
- Minimum: 8−3=5
- Maximum: 8+3=11
- For x2:
- Minimum: 4⋅(−1)=−4
- Maximum: 4⋅1=4
Step 6: Determine if there is an overlap in ranges
The range of x1 is from 5 to 11, and the range of x2 is from -4 to 4. Since there is no overlap between these ranges, the two particles will never collide.
Conclusion
Thus, the two particles will not collide at any time t. Therefore, the answer is:
The two particles will collide after time t=none of these (they never collide).
x2=4cos(ωt)
- Minimum: 8−3=5
- Maximum: 8+3=11
- Minimum: 4⋅(−1)=−4
- Maximum: 4⋅1=4
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Matrix matching type questions
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Integer type questions
14 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - More than one option is correct
50 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
x-t equation of a particle moving along x-axis is given as
x=A+A(1−cosωt)
View SolutionDisplacement-time equation of a particle executing SHM is x=4sin(ωt)+3sin(ωt+π/3)
Here, x is in cm and t ini sec. The amplitude of oscillation of the particle is approximately.
View SolutionThe velocity versus time graph of two particles moving along x-axis varies are shown in the following two plots. Then
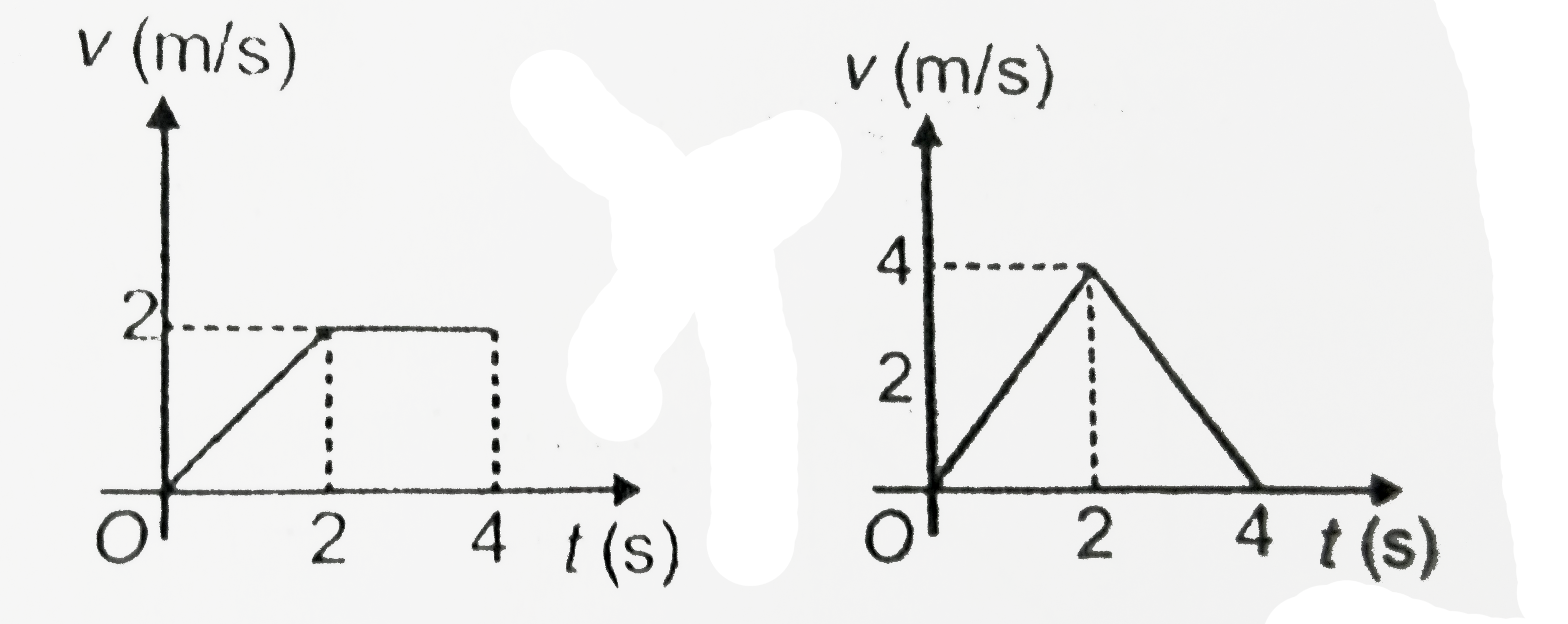
View SolutionThe position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View SolutionThe position x of particle moving along x-axis varies with time t as x=Asin(ωt) where A and ω are positive constants. The acceleration a of particle varies with its position (x) as
View SolutionThe position of a particle moving along x-axis varies with time t according to equation x=√3sinωt−cosωt where ω is constants. Find the region in which the particle is confined.
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is

View SolutionThe displacement of a particle along the x- axis it given by x=asin2ωt The motion of the particle corresponds to
View SolutionThe position of a particle moving in space varies with time t according as :−
x(t)=3cosωt
y(t)=3sinωt
z(t)=3t−8
where ω is a constant. Minimum distance of particle from origin is :−
View Solution
