The position x of particle moving along x-axis varies with time t as where A and are positive constants. The acceleration a of particle varies with its position (x) as
The correct Answer is:D
Step by step video & image solution for The position x of particle moving along x-axis varies with time t as x=Asin(omegat) where A and omega are positive constants. The acceleration a of particle varies with its position (x) as by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The position of a particle moving along x- axis is given by x=x0cos2(ωt) . Its when it is at mean position is
View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is

View SolutionPosition of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe velocity (υ) of a particle moving along X-axis varies with its position x as shown in figure. The acceleration (a) of particle varies with position (x) as
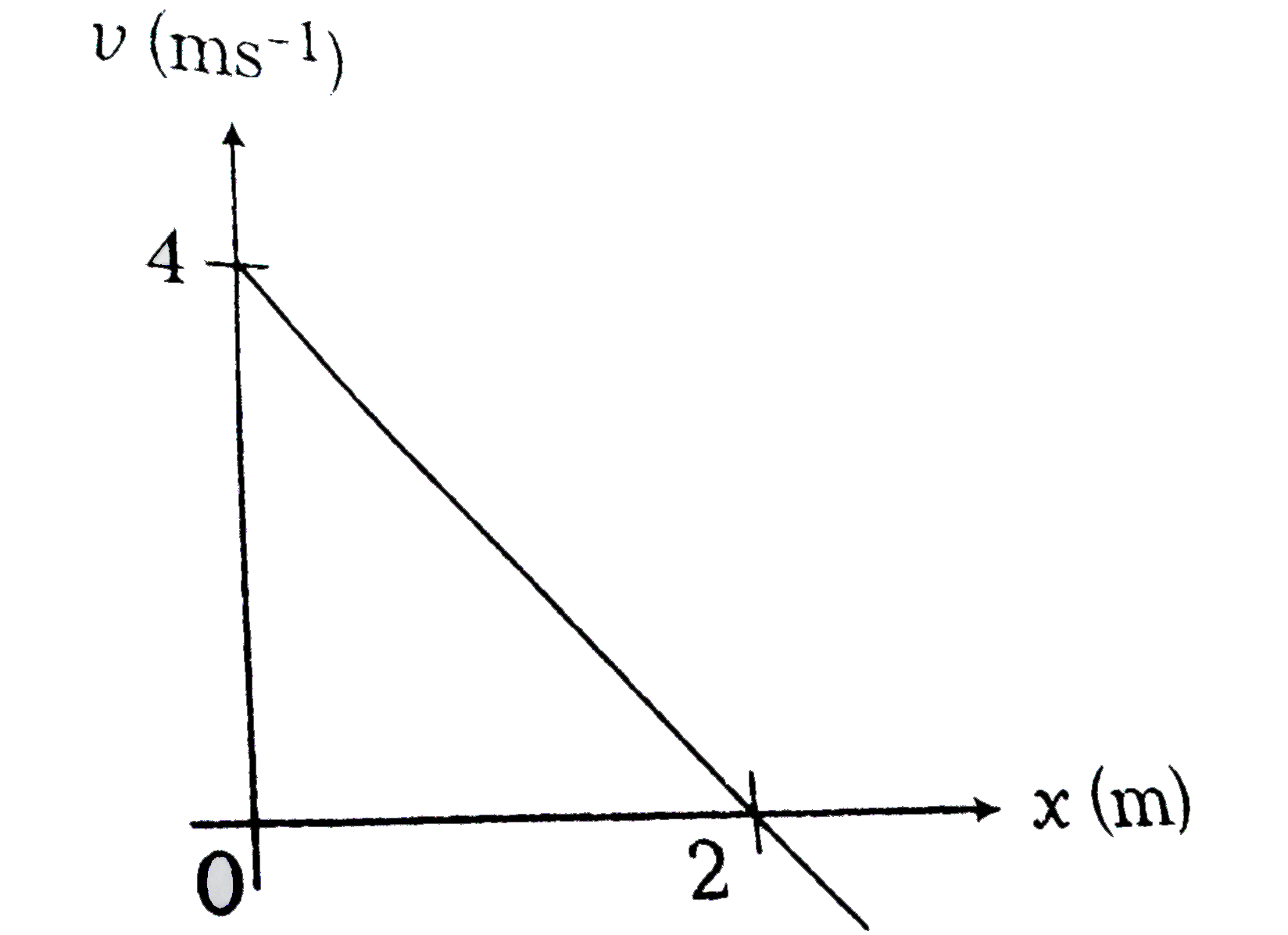
View SolutionThe position of a particle moving along x-axis varies with time t according to equation x=√3sinωt−cosωt where ω is constants. Find the region in which the particle is confined.
View SolutionThe position-time relation of a particle moving along the x-axis is given by
x=a−bt+ct2
where a, b and c are positive numbers. The velocity-time graph of the particle is
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionThe position of a particle moving in space varies with time t according as :−
x(t)=3cosωt
y(t)=3sinωt
z(t)=3t−8
where ω is a constant. Minimum distance of particle from origin is :−
View SolutionThe position vector of the particle is r(t)=acosωtˆi+asinωtˆj, where a and ω are real constants of suitable dimensions. The acceleration is
View SolutionThe position of a particle moving along x-axis varies eith time t as x=4t−t2+1. Find the time interval(s) during which the particle is moving along positive x-direction.
View Solution
