Plane-polarized light of wavelength 589nm propagates along the axis of a concentration 500g/l. Viewing from the side, one can see a system of helical fringes, with 50cm between neighbouring dark fringes along the axis. Explain the emergence of the fringes and determine the specific rotation consatnt of the solution.
Two effects are involved here : rotation of plane of polarization by sugar solution and the effect of that rotation on the scattering of light in the transverse direction. The latter is shown in the figure given below. It is easy to see from the figure that there will no scattering of light in this transverse direction if the incident light has its electric vector parallel to the line of sight. In such a situation, we expect fringes to occur in the given experiment.
From the given data see that in a disatnce of 150cm, the rotation of plane of polarization must be 180∘. Thus the specific rotation constant of suger
=rotation constantconcentration
=180/50500glang/deg/cm=1805.0dm×(.500gm/cc)
=72∘angdeg/(dmgm/cc)(1dm=10cm)

Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Optics Of Moving Sources
22 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Diffraction Of Light
60 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
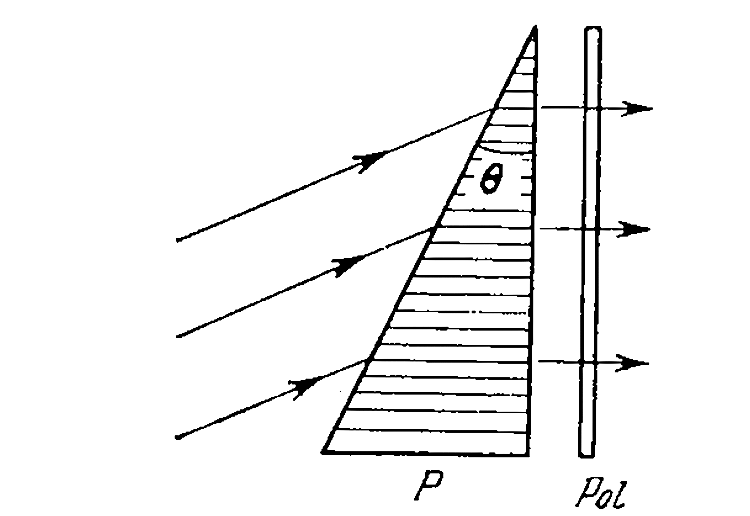
Plane-polarized light of wavelength 0.59μm falls on a trihedral quartz prism P (Fig.) with refracting angle Θ=30∘. Inside the prism light propagates along the optical axis whose direction is shwon by hatching. Behind the Polaroid Pol an interference pattern of bright and dark fringes of width Δx=15.0mm is pbserved. Find the specific rotation constant of quartz and the distribution of intensity of light behind the Polaroid.
View SolutionA block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown.
A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as λ0 and refractive index of plastic as μ
Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there.
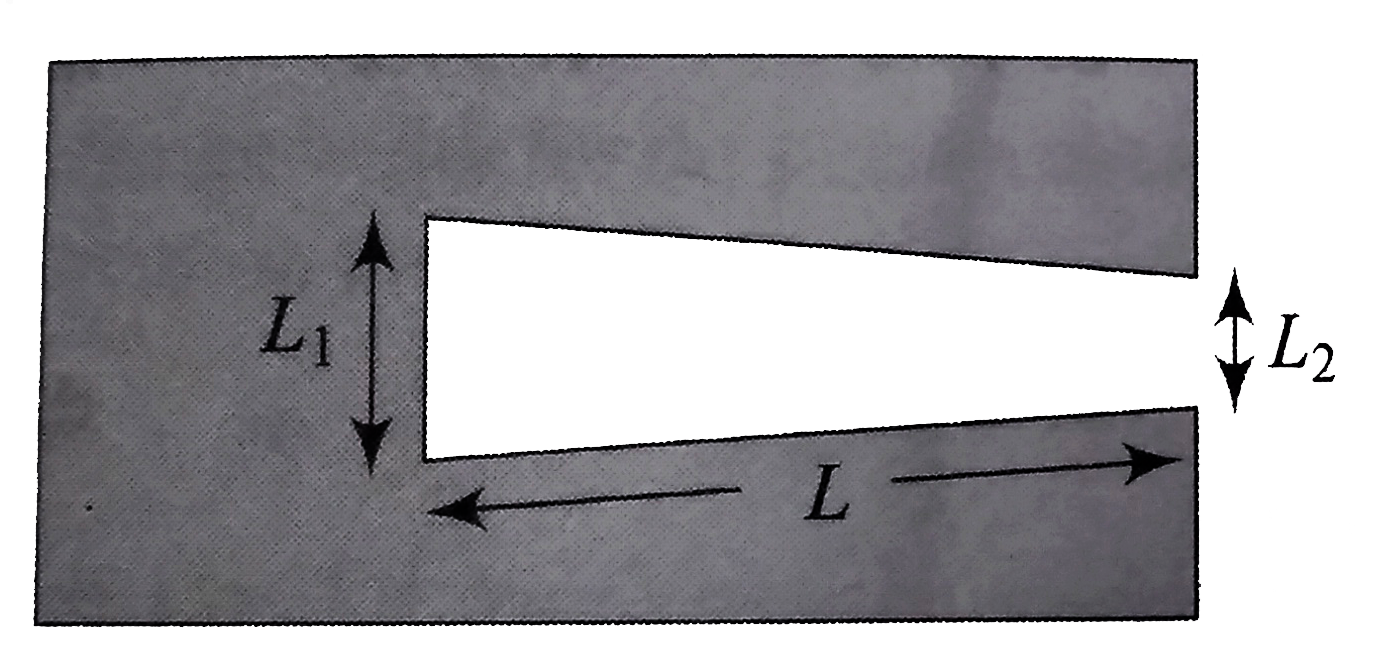
Determine the distance of 4th dark fringe from the left end of air cavity.
View Solution
Knowledge Check
A block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown.
A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as λ0 and refractive index of plastic as μ
Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there.

Determine the distance of 4th dark fringe from the left end of air cavity.A2L6+λ0BL1+3L4C4L7D5L7A block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown.
A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as λ0 and refractive index of plastic as μ
Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there.
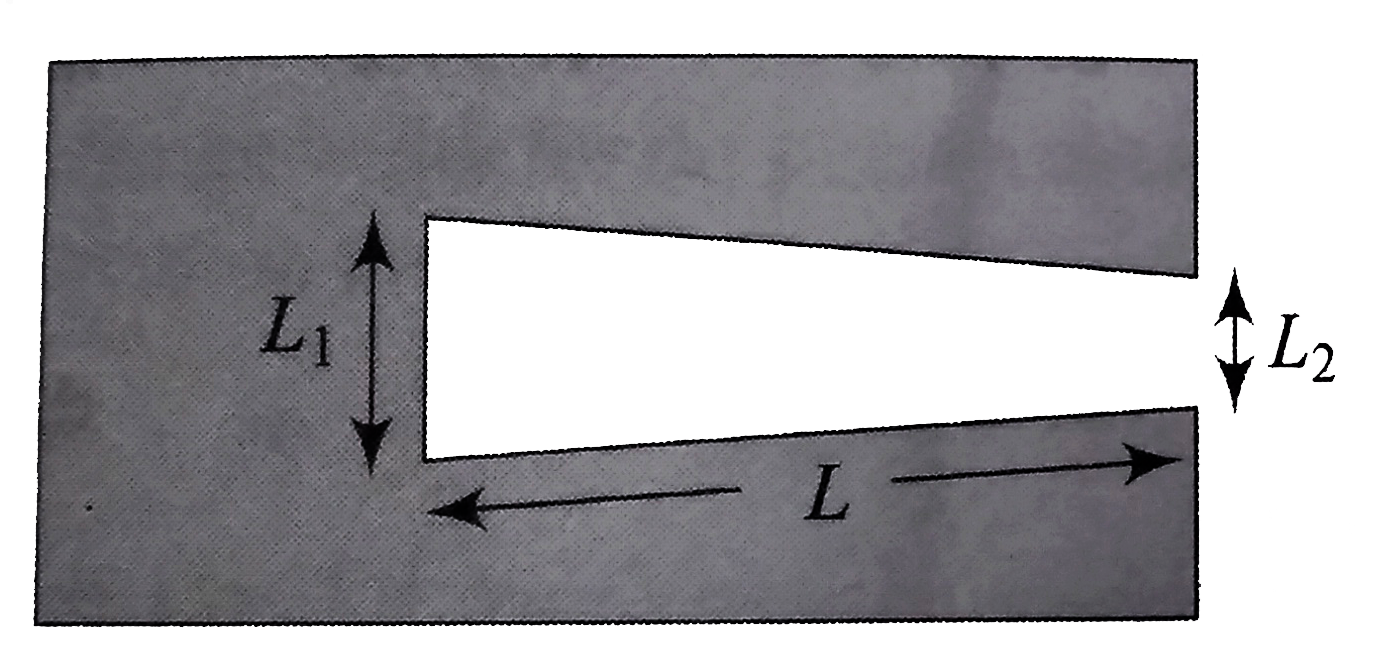
Determine of difference L1−L2=ΔL) in terms of λ0.A4λ0μB7λ02μC3λ0μDNone of the aboveA monochromatic light source S of wavelength 440 nm is placed slightly above a plane mirror M as shown . Image of S in M can be used as a virtual source to produce interference fringes on the screen. The distance of source S from O is 20.0 cm, and the distance of screen from O is 100.0 cm (figure is not to scale). If the angle θ=0.50×10−3 radians, the width of the interference fringes observed on the screen is –
 A2.20 mmB2.64 mmC1.10 mmD0.55 mm
A2.20 mmB2.64 mmC1.10 mmD0.55 mm
A block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown.
A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as λ0 and refractive index of plastic as μ
Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there.

Determine of difference L1−L2=ΔL) in terms of λ0.
View SolutionIn YDSE, two slits are separated by 3mm and illuminated by light of wavelength 480nm. The screen is 2m from the plane of slits. Calculate the separation between 8th bright fringe and 3rd dark fringe observed on the same side of central bright fringe.
View Solution(a) In Young's double slit experiment, a monochromatic source of light S is kept equidistant from the slits S1andS2. Explain the information of dark and bright fringes on the screen.
(b) A beam of light consisting of two wavelength, 650 nm and 520 nm, is used to obtain interference fringes in a Young's double - slit experiment.
(i) Find the distance of the third bright fringe on the screen from the central maximum for wavelengths 650 nm.
(ii) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide ?
Given: The seperation between the slits is 4 mm and the distance between the screen and plane of the slits is 1.2 m.
View SolutionA light bulb shines light along the x axis and through two parallel ideal polarizing filters one with a fixed polarizing axis and the other with an axis that rotates about the x axis and the yz plane . Looking toward the light bulb through the combined filtering system you see
View SolutionA block o plastic having a thin air cavity (whose thickenss is comparable to wavelength of light waves) is shown in fig. The thickness of air cavity (which can be considered as air wedge for interference pattern) is varying linearly from one end to other as shown.
A broad beam of monochromatic light is incident normally from the top of the plastic box. Some ligth lis reflected back above and below the cavity .The plastic layers than wavelength of incident light . An observer when looking down from top sees an interference pattern consisting of eight dark fringes and seven bright fringe along the wedge. Take wavelength of incident light in air as λ0 and refractive index of plastic as μ
Assume that the thickness of the ends of air cavity are such that formation of fringe takes place there.

Determine the separation between 1st and 2nd dark fringes form the left end of air cavity
View Solution
