Prove that in charging a capacitor half of the energy supplied by the battery is stored in the capacitor and remaining half is lost during charging.
To prove that in charging a capacitor, half of the energy supplied by the battery is stored in the capacitor and the remaining half is lost during charging, we can follow these steps:
Step 1: Determine the Energy Supplied by the Battery
When a capacitor of capacitance C is connected to a battery with voltage V, the total charge Q on the capacitor is given by:
Q=CV
The energy supplied by the battery (UB) when charging the capacitor can be calculated as:
UB=Q⋅V
Substituting Q from the first equation:
UB=(CV)⋅V=CV2
This is our Equation 1.
Step 2: Calculate the Energy Stored in the Capacitor
The energy stored in the capacitor (UC) can be derived using the concept of integration. The energy stored in a capacitor is given by:
UC=∫Q0VdQ
Since V across the capacitor varies as it charges, we can express V in terms of Q:
V=QC
Thus, the energy stored becomes:
UC=∫Q0QCdQ
Calculating this integral:
UC=1C∫Q0QdQ=1C(Q22)Q0=Q22C
Substituting Q=CV:
UC=(CV)22C=12CV2
This is our Equation 2.
Step 3: Compare the Energy Supplied and Stored
From Equations 1 and 2, we have:
- Energy supplied by the battery: UB=CV2
- Energy stored in the capacitor: UC=12CV2
Step 4: Calculate the Energy Lost
The energy lost during the charging process can be calculated as:
Energy lost=UB−UC=CV2−12CV2=12CV2
Conclusion
Thus, we have shown that:
- Half of the energy supplied by the battery is stored in the capacitor: UC=12UB
- The remaining half is lost during charging: Energy lost=12UB
Therefore, it is proved that during the charging of a capacitor, half of the energy supplied by the battery is stored in the capacitor and the remaining half is lost.
When a capacitor of capacitance C is connected to a battery with voltage V, the total charge Q on the capacitor is given by:
Q=CV
The energy supplied by the battery (UB) when charging the capacitor can be calculated as:
UB=Q⋅V
Substituting Q from the first equation:
UB=(CV)⋅V=CV2
This is our Equation 1.
The energy stored in the capacitor (UC) can be derived using the concept of integration. The energy stored in a capacitor is given by:
UC=∫Q0VdQ
Since V across the capacitor varies as it charges, we can express V in terms of Q:
V=QC
Thus, the energy stored becomes:
UC=∫Q0QCdQ
Calculating this integral:
UC=1C∫Q0QdQ=1C(Q22)Q0=Q22C
Substituting Q=CV:
UC=(CV)22C=12CV2
This is our Equation 2.
From Equations 1 and 2, we have:
- Energy supplied by the battery: UB=CV2
- Energy stored in the capacitor: UC=12CV2
The energy lost during the charging process can be calculated as:
Energy lost=UB−UC=CV2−12CV2=12CV2
Thus, we have shown that:
- Half of the energy supplied by the battery is stored in the capacitor: UC=12UB
- The remaining half is lost during charging: Energy lost=12UB
Topper's Solved these Questions
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
155 Videos
- CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE
1 Videos
- ATOMSBOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY
42 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
Similar Questions
Find the charge stored in the capacitor.
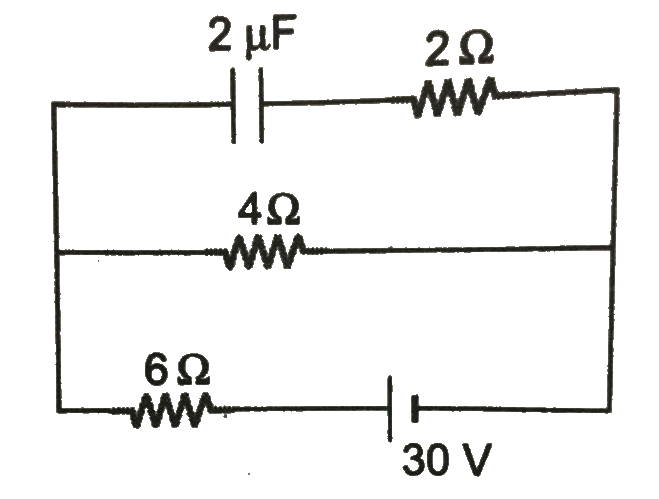
View SolutionFind the charge stored in the capacitor.
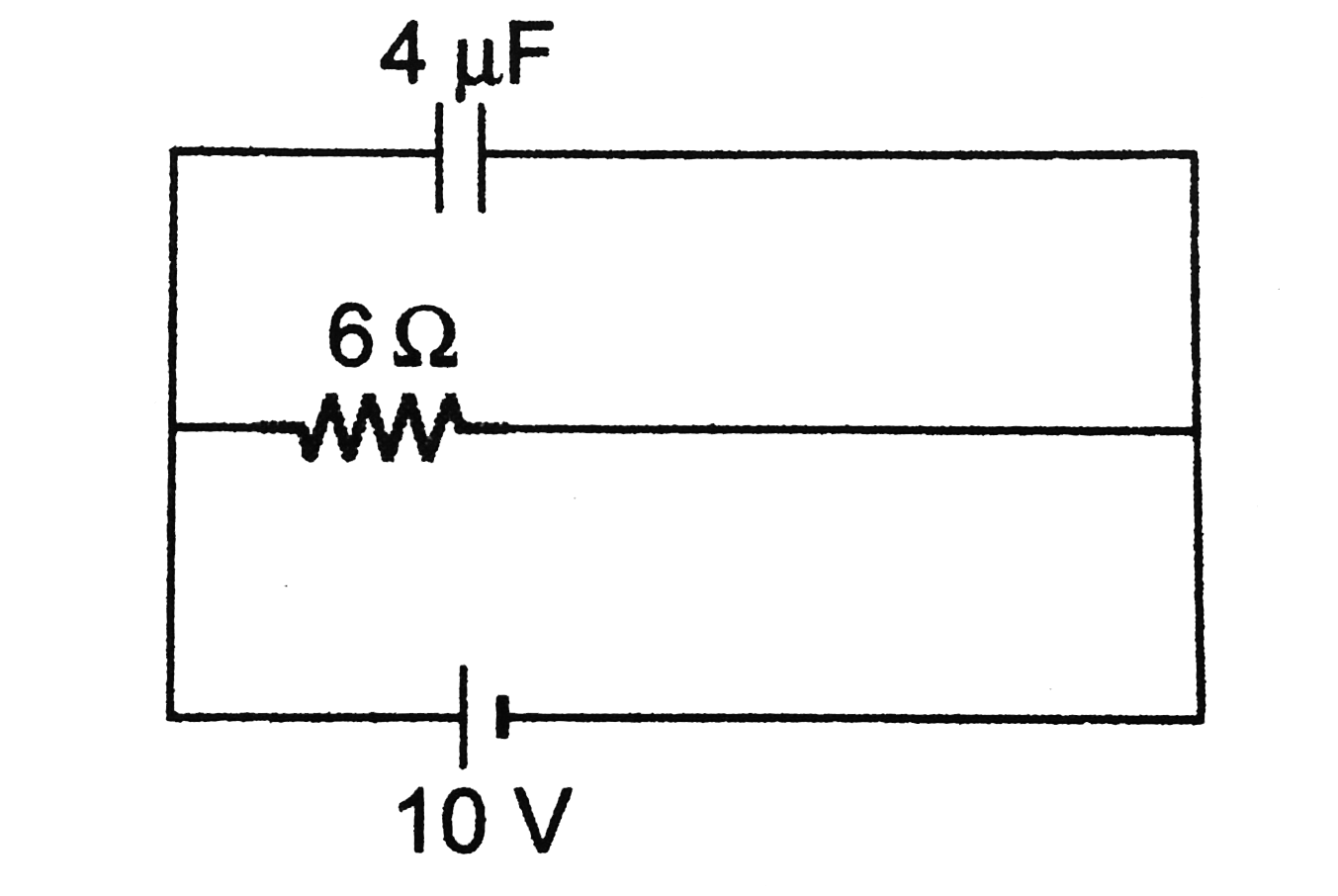
View SolutionFind the charge stored in the capacitor.
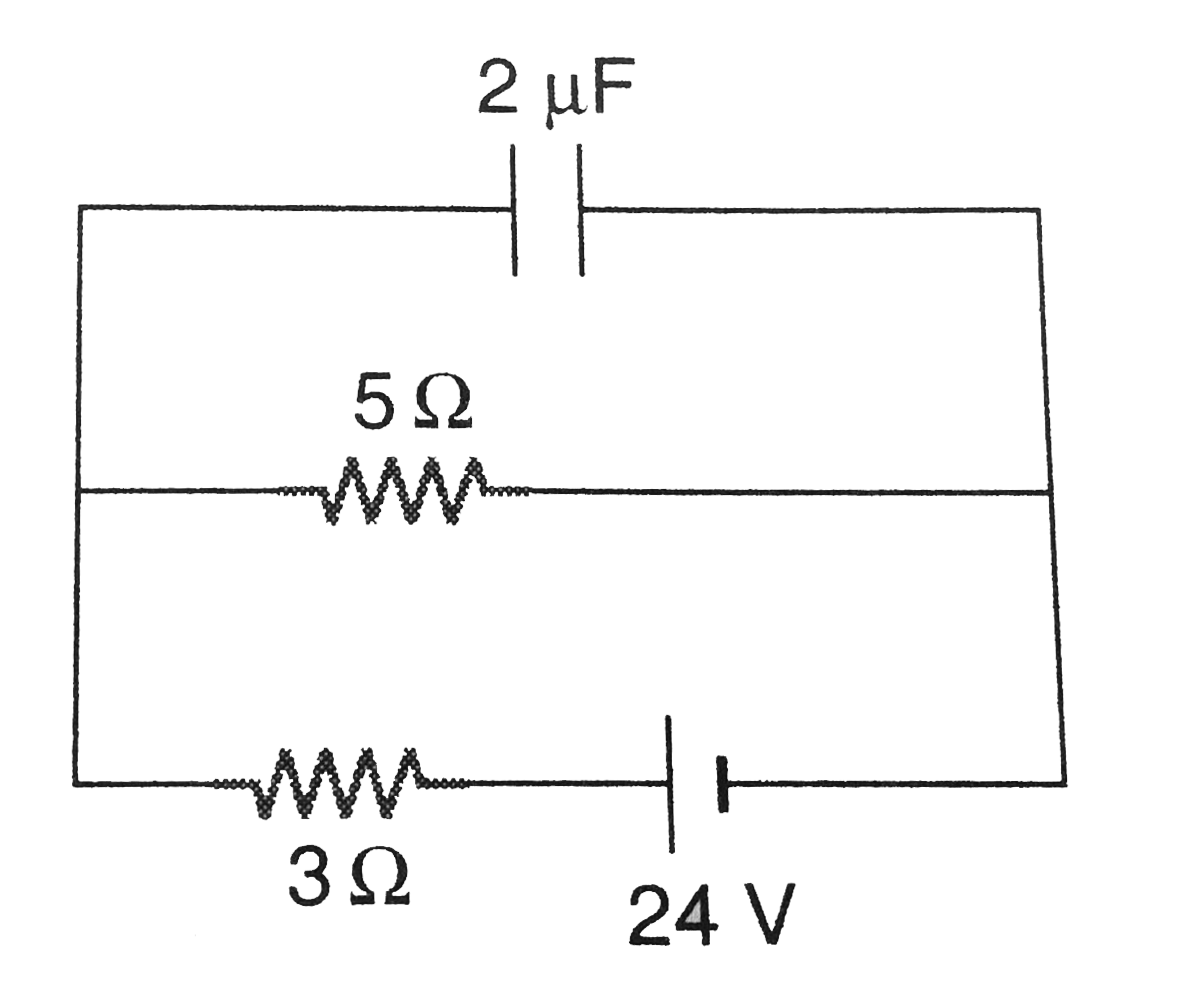
View SolutionAssertion : When a capacitor is charged by a battery. Half of the energy supplied by the battery is stored in the capacitor and rest half is lost.
Reason : If resistance in the circuit is zero, then there will be no loss of energy.
View SolutionFind the charged stored in all the capacitors
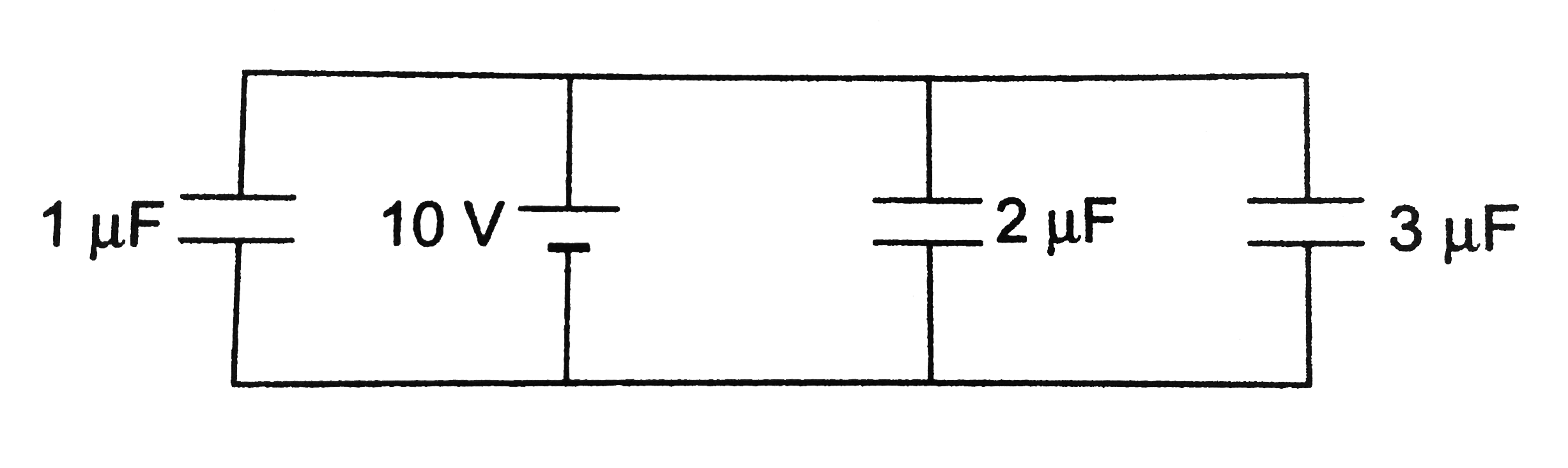
View SolutionIn a charged capacitor, the energy resides in
View SolutionAssertion : When an uncharged capacitor is charged by a battery only 50% of the energy supplied is stored in the capacitor.
Reason : Rest 50% is lost.
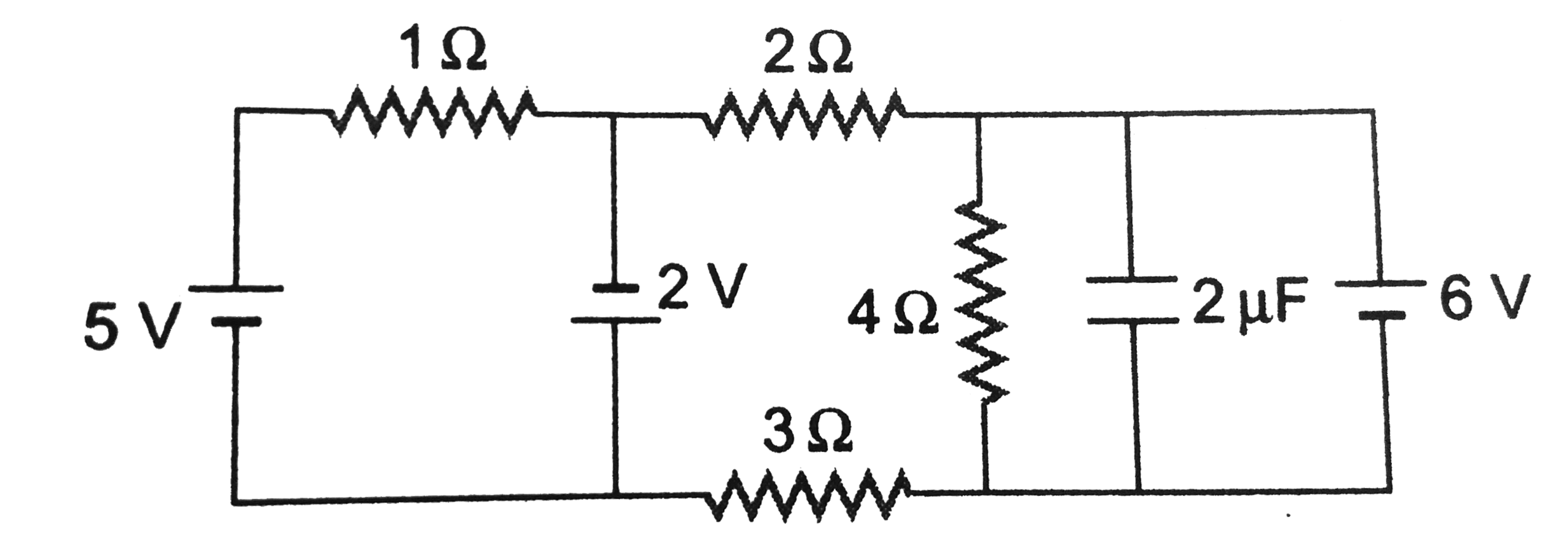
View SolutionThe current in 1Ω resistance and charge stored in the capacitor are
View SolutionA battery does 200 J of work in charging a capacitor. The energy stored is.
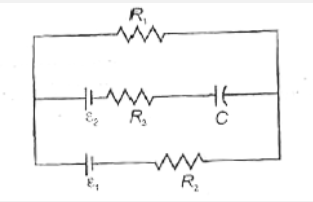
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
View Solution
