A battery does 200 J of work in charging a capacitor. The energy stored is.
200 J
100 J
50 J
400 J
The correct Answer is:B
To find the energy stored in a capacitor when a battery does 200 J of work in charging it, we can follow these steps:
1. Understand the Work Done by the Battery:
The work done (W) by the battery in charging the capacitor is given as 200 J. This work done is equal to the charge (Q) multiplied by the voltage (V) across the capacitor.
W=Q×V
Here, we have:
W=200J
2. Energy Stored in the Capacitor:
The energy (U) stored in a capacitor can be calculated using the formula:
U=12CV2
However, we can also express this in terms of charge (Q) and voltage (V). Since Q=C×V, we can substitute this into the energy formula:
U=12QV
3. Substituting Work Done into the Energy Formula:
From the work done by the battery, we know that Q×V=200J. Therefore, we can substitute this into our energy formula:
U=12(Q×V)=12×200J
4. Calculating the Energy Stored:
Now, we can calculate the energy stored in the capacitor:
U=12×200=100J
5. Conclusion:
Thus, the energy stored in the capacitor is:
U=100J
Final Answer:
The energy stored in the capacitor is 100 Joules.
The work done (W) by the battery in charging the capacitor is given as 200 J. This work done is equal to the charge (Q) multiplied by the voltage (V) across the capacitor.
W=Q×V
Here, we have:
W=200J
The energy (U) stored in a capacitor can be calculated using the formula:
U=12CV2
However, we can also express this in terms of charge (Q) and voltage (V). Since Q=C×V, we can substitute this into the energy formula:
U=12QV
From the work done by the battery, we know that Q×V=200J. Therefore, we can substitute this into our energy formula:
U=12(Q×V)=12×200J
Now, we can calculate the energy stored in the capacitor:
U=12×200=100J
Thus, the energy stored in the capacitor is:
U=100J
The energy stored in the capacitor is 100 Joules.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - B
Explore 38 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - C
Explore 53 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:EXERCISE
Explore 20 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT SECTION - D Assertion-Reason Type Questions
Explore 25 Videos
- GRAVITATION Book:AAKASH INSTITUTE ENGLISHChapter:GRAVITATION Exercise:ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
Explore 15 Videos
Similar Questions
Three capacitors of capacitances 3μF, 6μF, and 4μF are connected as shown across a battery of emf 6V.
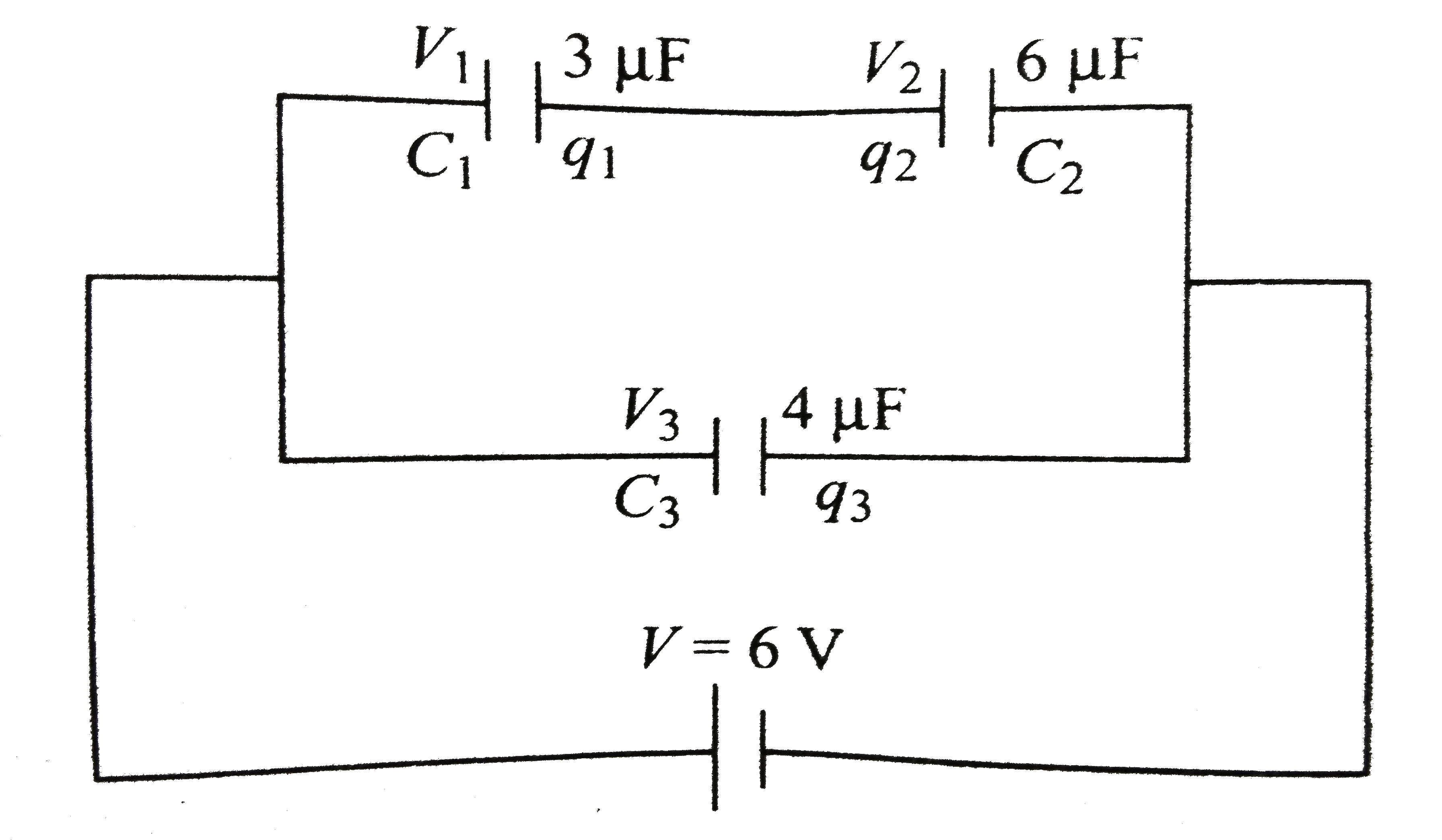 .
.
i. Find the equivalent capacitance,
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in the system of capacitors and total energy stored in the system of capacitor.
View SolutionHow many percent of work done by a battery is consumed to fully charge a capacitor which is stored as electric potential energy in the capacitor ?
View SolutionThe capacitance of a charged capacitor is C and the energy stored in it is U. What is the value of charge on the capacitor?
View SolutionProve that in charging a capacitor half of the energy supplied by the battery is stored in the capacitor and remaining half is lost during charging.
View SolutionDiscuss the similarities between the energy stored in the electric field of charged capacitor and the energy stored in the magnetic field of a current-carrying coil.
View SolutionThree capcitors of capacitances 4μF,
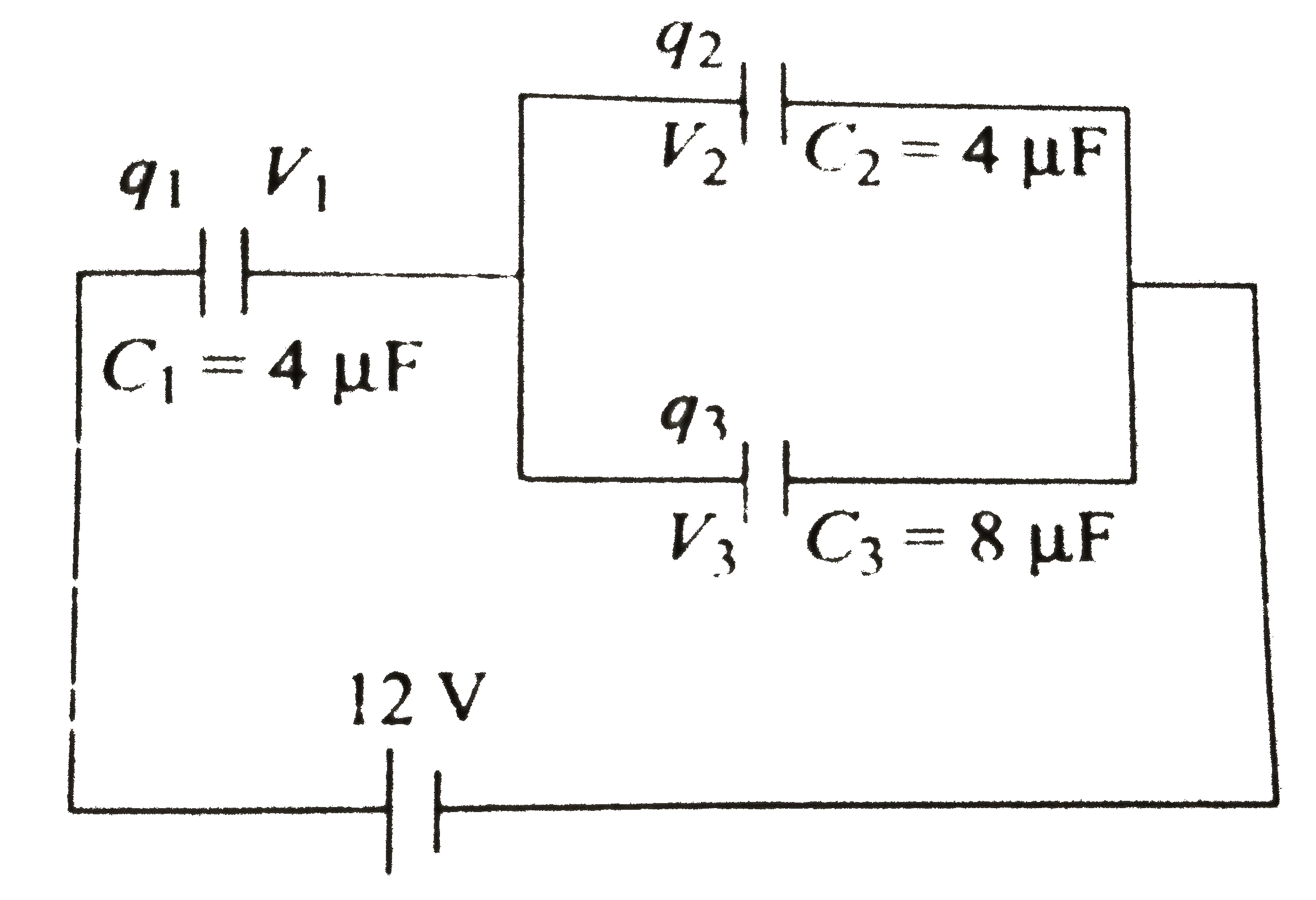 .
.
4μF, and 8μF, are connected as show across a battery of emf 12V.
i. Find the equivalent capacitane.
ii. Find the potential difference and charge on each capacitor.
iii. Find the energy stored in each capacitor and the total energy stored in the system of capacitors.
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionIn an oscillating LC circuit the maximum charge on the capacitor is Q. The charges on the capacitor when the energy is stored equally between the electric and magnetic field is
View SolutionA capacitor is charged using a a battery and energy stored is U. After disconnecting the battery another uncharged capacitor of same capacitance is connected in parallel to the first capacitor. Then loss of energy is equal to
View SolutionIn oscillating Lc circuit, the total stored energy is U and maximum charge upon capacitor is Q2, the energy stored in the inductor is
View Solution
