Prove that total produced in different resistors of the circuit is minimum when the current is divided into a number of braches .
Text Solution
When the current is divided into a number if parallel braches , then I=I1+I2
Heat produced in the circuit in time t ,
H=I21r1tJ+(I−I1)2r2tJ

Differentiating both side with respect to I1,
dHdI1=2I1r1tJ−2(I−I1)r2tJ
When heat generated in the circuit is minimum ,
dHdI1=0 or, 2I1r1tJ−2(I−I1)r2tJ=0
or , 2I1r1tJ=2(I−I1)r2tJ= or, I1r1=(I−I1)r2=I2r2
∴I1I2=r2r1
i.e., the heat produed in the circuit will be minimum if the current is divided into the braches such that the current in each branch is inversely proportional to the resistance .
|
Topper's Solved these Questions
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - EXERCISE (Multiple Choice Question )
10 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - EXERCISE (Very Short Answer Type Questions )
18 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - Section Related Questions
21 Videos
- DIGITAL CIRCUITS BOOK - CHHAYA PUBLICATIONCHAPTER - DIGITAL CIRCUITS EXERCISE - CBSE SCANNER
6 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - CBSE SCANNER
31 Videos
Similar Questions
Knowledge Check
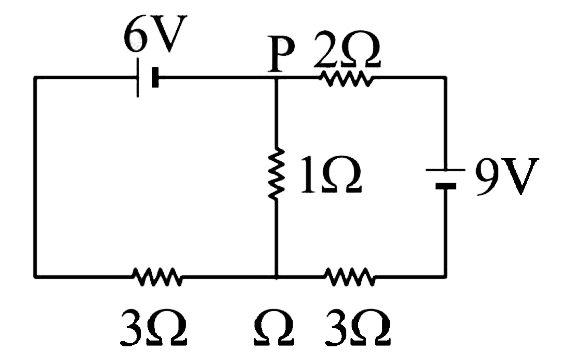
In the circuit shown, the current in the 1Ω resistor is :
 A0.13A,omQ→PB0.13A,omP→QC1.3AomP→QD0A
A0.13A,omQ→PB0.13A,omP→QC1.3AomP→QD0AThe total heat produced in resistor r in an RL circuit when the current in the inductor decreases from Io to 0 is
ALI20B12LI20C32LI20D13LI20
In the circuit shown, the current in the 1Ω resistor is :

View SolutionIn the circuit shown, the current in the 1Ω resistor is :
View SolutionThe current in the resistor R3 in the circuit as shown in the figure is

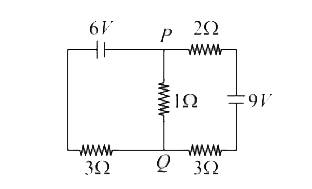
View SolutionIn the circuit shown, the current in the 1Ω resistor is

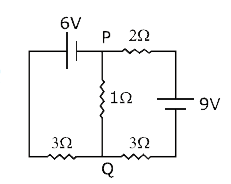
View SolutionIn the circuit shown , the current in the 1Ω resistor is :
View SolutionThe total heat produced in resistor r in an RL circuit when the current in the inductor decreases from Io to 0 is
View Solution