The total heat produced in resistor r in an RL circuit when the current in the inductor decreases from Io to 0 is
LI20
12LI20
32LI20
13LI20
The correct Answer is:B
To find the total heat produced in a resistor R in an RL circuit when the current in the inductor decreases from I0 to 0, we can follow these steps:
1. Understanding the Power Dissipation:
The power P dissipated in the resistor R is given by the formula:
P=I2R
where I is the current flowing through the resistor.
2. Current Decay in the RL Circuit:
In an RL circuit, the current I(t) at time t when the switch is opened (or when the current is decreasing) is given by:
I(t)=I0e−RLt
where I0 is the initial current, R is the resistance, and L is the inductance.
3. Total Energy (Heat) Calculation:
The total energy W dissipated in the resistor as heat when the current changes from I0 to 0 can be found by integrating the power over time:
W=∫∞0Pdt=∫∞0I2Rdt
Substituting I(t):
W=∫∞0(I0e−RLt)2Rdt
W=RI20∫∞0e−2RLtdt
4. Evaluating the Integral:
The integral ∫∞0e−2RLtdt can be evaluated as follows:
\int_0^\infty e^{-kt} \, dt = \frac{1}{k} \quad \text{(where k = \frac{2R}{L} )}
Thus,
∫∞0e−2RLtdt=L2R
5. Substituting Back:
Now substituting this result back into the expression for W:
W=RI20⋅L2R
The R cancels out:
W=12I20L
6. Final Result:
Therefore, the total heat produced in the resistor R when the current decreases from I0 to 0 is:
W=12LI20
Final Answer:
The total heat produced in the resistor R is 12LI20.
The power P dissipated in the resistor R is given by the formula:
P=I2R
where I is the current flowing through the resistor.
In an RL circuit, the current I(t) at time t when the switch is opened (or when the current is decreasing) is given by:
I(t)=I0e−RLt
where I0 is the initial current, R is the resistance, and L is the inductance.
The total energy W dissipated in the resistor as heat when the current changes from I0 to 0 can be found by integrating the power over time:
W=∫∞0Pdt=∫∞0I2Rdt
Substituting I(t):
W=∫∞0(I0e−RLt)2Rdt
W=RI20∫∞0e−2RLtdt
The integral ∫∞0e−2RLtdt can be evaluated as follows:
\int_0^\infty e^{-kt} \, dt = \frac{1}{k} \quad \text{(where k = \frac{2R}{L} )}
Thus,
∫∞0e−2RLtdt=L2R
Now substituting this result back into the expression for W:
W=RI20⋅L2R
The R cancels out:
W=12I20L
Therefore, the total heat produced in the resistor R when the current decreases from I0 to 0 is:
W=12LI20
The total heat produced in the resistor R is 12LI20.
Topper's Solved these Questions
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (multiple Correct )
7 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (assertion-reasoning)
2 Videos
- INDUCTANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Exercises (subjective)
7 Videos
- HEATING EFFECT OF CURRENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit
27 Videos
- MAGNETIC FIELD AND MAGNETIC FORCESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type
2 Videos
Similar Questions
The current in the resistor R3 in the circuit as shown in the figure is

View SolutionIn the circuit shown, the current I will be zero when R is
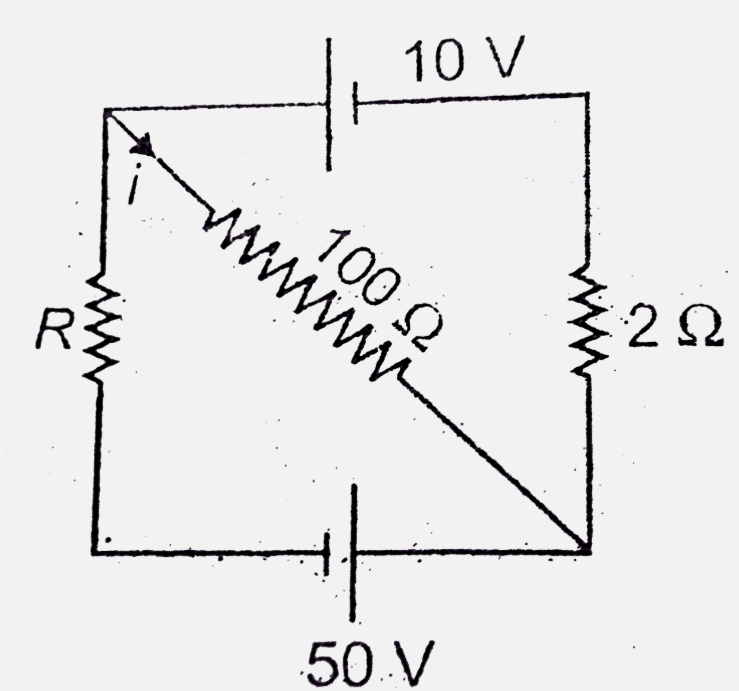
View SolutionResistors of 1, 2, 3 ohm are connected in the form of a triangle. If a 1.5V cell of negligible internal resistance is connected across 3 ohm resistor, the current flowing through this resistance will be
View SolutionIn a circuit shown if figure , the heat produced in 3 ohm resistor due to a current flowing in it is 12 J. The heat produced In 4 ohm resistor is .
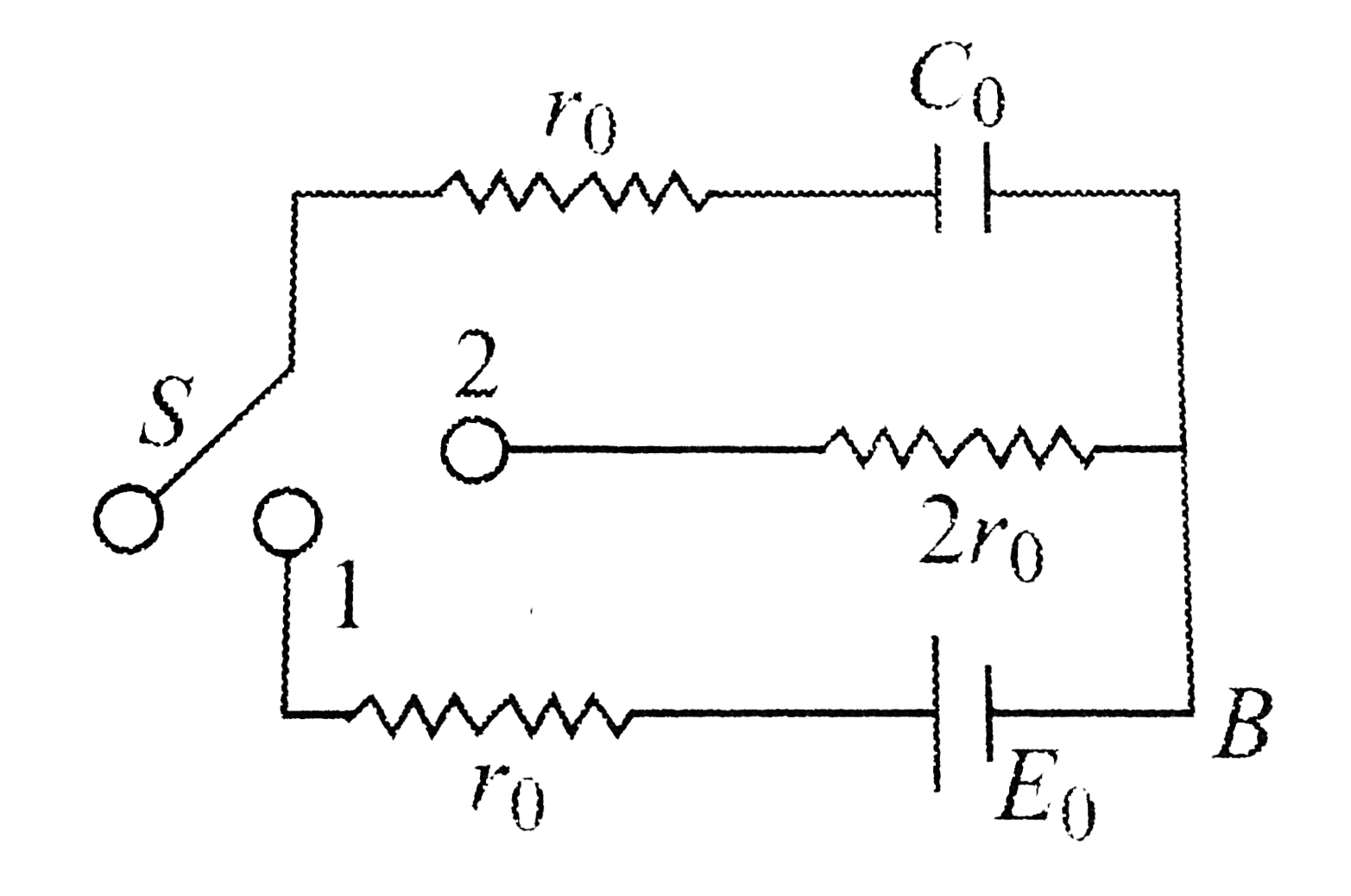
View SolutionIn the circuit given in fig. swithc S is at position 1 for long time. Find the total heat generated in resistor of resistance (2r0), when the switch S is shifted from position 1 to position 2.
View SolutionIn the following circuit (Fig.)the switch is closed at t=0. Intially, there is no current in inductor. Find out the equation of current in the inductor coil as s function of time.
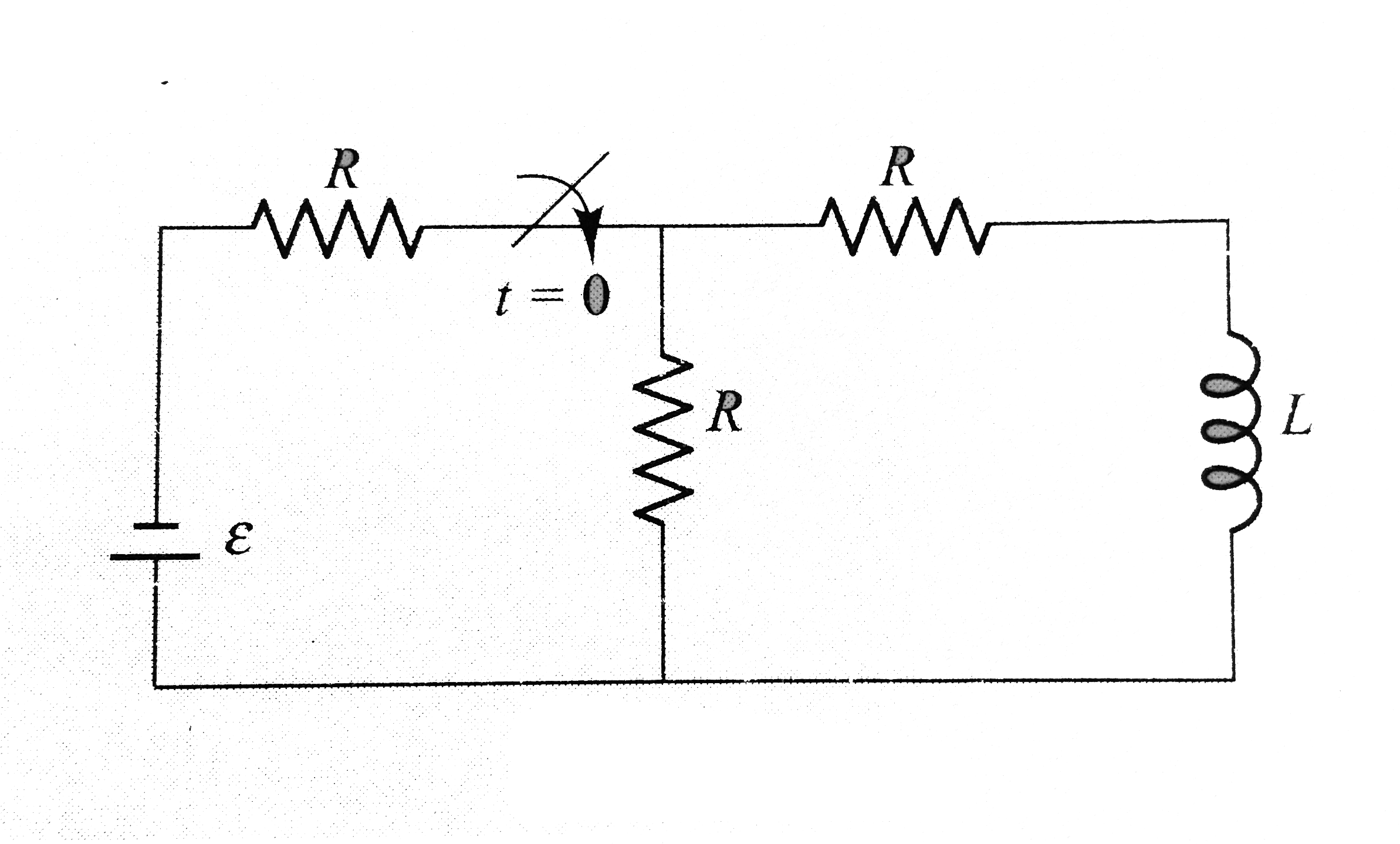
View SolutionIn the circuit shown in Fig.6.2, the heat produced in 5Ω resistor, due to the current flowing through it is 10 calorie per second. Find the heat produced in 4Ω resistor.
View SolutionIn the circuit shown in fig the heat produced in the 5 ohm resistor due to the current flowing through it is 10 calories per second.
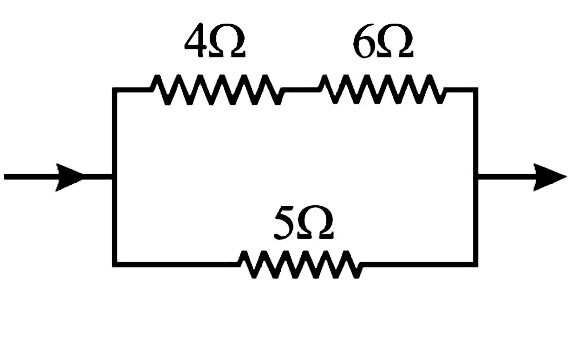
The heat generated in the 4 ohms resistor is
View SolutionThe heat produced (in calories) in a resistance R when a current I amperes flows through it for t seconds is given by the expression
View SolutionIf V0 and I0 are the peak current and voltge across the resistor in a series L−C−R circuit, then the power dissipated in the circuit is (powerfac→r=cosθ)
View Solution
