Prove the following formula when refraction takes place at a convex spherical refracting surface and source of light lies in the rarer medium and image formed is real μ2v−μ1u=μ2−μ1R Where the terms have their usual meanings.Solution in Punjabi
Assumptions: (i) The object is a point object and lying on the principal axis.
(ii) The aperature of refracting spherical surface is small.
(iii) The incident ray, refracted ray and normal make smaller angles with principal axis.
Cartesian sign conventions,
(i) All the distances are measured from the pole of the spherical surface.
(ii) The distances measured along the incident ray are taken as positive and distances measured opposites to direction of incident ray are taken as negative.
(iii) The distances measured in vertically upward direction from principal axis are taken as positive and in vertically downward direction from principal axis are taken as negative.
Consider a convex spherical refracting surface of refractive index μ2. Let it be placed in a rarer medium of refractive index μ1(μ2>μ1).
A point object O lies on the principal axis at a distance u from the pole of the convex refracting surface in rarer medium. A ray of light from O incident the convex surface at A. AC is the normal to the convex surface. After refraction at A, the ray enters the dense medium and bends towards the normal. The refracted ray meets the principal axis at I which is the real image of the object O. The distance of the image I from the pole of the convex surface is V.
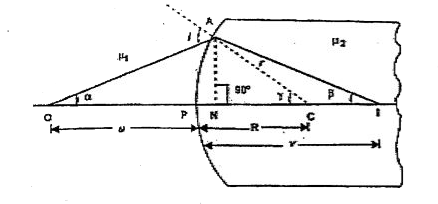
d Let α,β and γ be the angles made by the incident ray, refracted ray and the normal respectively with the principal axis. Draw AN perpendicular on the principal axis.
From ΔAOE i=α+γ.............i
Since α,β and γ are small angles (assumption) so they can be replaced by their tangents,
Hence eqn (i) becomes
i=tanα+tanγ................ii
From ΔAIC γ=r+β or r=γ−β...........iii
Again γ and βs are small (assumption) so they can be replaced by their tangents. HEnce eq (iii) becomes
r=tanγ−tanβ ............iv
Determination of tanα,tanβ and tanγ
From rt. ∠dΔANO tanα=ANNO............v
From rt. ∠dΔANC, tanγ=ANNC..........vi
From rt. ∠dΔANI tanβ=ANNI.............vii
Using eqns v to vi we can writes eqn (iii) and (iv) as
i=ANNO+ANNC......................viii and r=ANNC−ANNI..........ix
Since aperture of the spherical surface is small (assumption) so point N lies very close to point P.
∴NO=PO,NC≅PC and NI≅PI
Hnece eqn viii and ix can be written as
i=ANPO+ANPC.........x
and r=ANPC−ANPI ...........xi
Now according to Snell.s law
sinisinr=μ2μ1 orμ1sini=μ2sinr
∴i and r are small angles
so sin i=i and sin r=r
⇒μ1i=μ2r
Using eqns (x) and (xi)
μ1[ANPO+ANPC]=μ2[ANPI−ANPC]
⇒μ1PO+μ1PC=μ2PI−μ2PC.....xii
Applying sign conventions
PO=−u,PC=R,PI=−v
From eqn xii
μ1−u+μ1R=μ2−v+μ2R
⇒−μ1u+μ2v=μ2R−μ1R
−μ1u+μ2v=μ2−μ1R
Divide all the terms on both sides by μ1 we have −1u+μ2/μ1v=μ2/μ1−1R
But μ2μ1=1μ2=μ= Refractive index of medium 2 w.r.t medium 1.
⇒−1u−μv=μ−1R
Topper's Solved these Questions
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - NUMERICAL PROBLEMS36videos
REFRACTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFRACTION OF LIGHTEXERCISE - SHORT ANSWER TYPE QUESTIONS19videos
REFRACTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - REFLECTION OF LIGHT EXERCISE - NUMERICALS PROBLEMS7videos
REFLECTION OF LIGHT
- BOOK - BETTER CHOICE PUBLICATIONCHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Most Expected Questions6videos
SEMI CONDUCTOR DEVICES
Similar Questions
A convex lens of refractive index 1.5 has a focal length of 18 cm in air.Calculate the change in focal length,when it is immersed in water of refractive index 4/3.
02:05View SolutionWhat is meant by power of a lens? What does its sign indicate? State it SI unit, how is it related to the focal length of a lens?
07:16View SolutionA 5 cm long needle lies along the principal axis axis of a concave miror of focal length 20 cm in such a way that the end closer to the pole is 40 cm from it.Find the length of the image of the needle formed by the mirror.
08:48View SolutionCan two P-N junction diodes back to back works as P-N-P transistor?
01:45View SolutionThe equation of refraction at a spherical surface is μ2v−μ1u=μ2−μ1R
Taking R=∞, show that this equation leads to the equation
RealdepthApparentdepth=μ2μ1 for fraction at a plane surface.07:59View SolutionFigure shows figure three transparent medi of refractive indices μ1,μ2andμ3. A point object O is placed in the medium μ2. If the entire medium on the right of the spherical surface has refractive index μ1, the image forms at O. If this entire medium has refractive index μ2 the image form at O''. In the situation shown
 10:18View Solution
10:18View SolutionProve that −μ1u+μ2v=μ2−μ1R when refraction occurs from rarer to denser medium at a concave spherical refracting surface.
06:18View SolutionWhen refraction occurs from denser to……….., then (mu_2)/(mu_1) = …………. .
03:19View SolutionFigure shows three transparent media of refractive indices μ1,μ2andμ3. A point object O is placed in the medium μ2. If the entire medium on the right of the spherical surface has refractive index μ1, the image forms at O'. If this entire medium has refractive index μ3 the image form at O''. In the situation shown
 01:58View Solution
01:58View SolutionProve the following formula when refraction takes place at a convex spherical refracting surface and source of light lies in the rarer medium and image formed is real μ2v−μ1u=μ2−μ1R Where the terms have their usual meanings.
02:30View SolutionStarting new cartesian sign conventions, derive the relation. -frac(mu_1)(u) + frac(mu_2)(v) = frac(mu_2-mu_1)(R) , when refraction occurs from rarer to denser medium at convex spherical refracting surface (mu_1 lt mu_2) . Where u, v and R are object distance, image distance and radius of curvature of spherical surface respectively.
07:44View SolutionA convex lens made of a material of refractive index μ1 , is kept in a medium of refractive index μ2, Parallel rays of light are incident on the lens. Complete the pathof rays of light emerging from the convex lens if μ1=μ2.
View SolutionA convex lens made of a material of refractive index 'mu_1' is kept in a medium of refractive index μ2, Parallel rays of light are incident on the lens. Complete the pathof rays of light emerging fromthe convex lens if μ1<μ2.
02:51View SolutionA convex lens made of a material of refractive index μ1 is kept ih a medium of refractive index μ2, Parallel rays of light are incident on the lens. Complete the path of rays of light emerging fromthe convex lens if μ1>μ2.
02:13View SolutionDerive the relation:- frac(mu_2)(v) - frac(mu_1)(u) = frac(mu_2 - mu_1) (R) when light undergoes refraction fromoptically rarer to optically denser medium at curved surface.
07:08View SolutionFigure shows three transparent media of refractive indices μ1,μ2andμ3 A point object O is placed in the medium. IF the entire medium on the right of the spherical surface has refractive index. μ1 the image forms at O. If this entire medium has refractive index μ3 the image forms at O. In the situation shown,
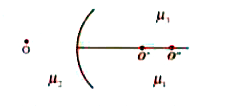 02:13View Solution
02:13View Solution

