Radiations of frequency 1015Hz is incident on three photosenstive surfaces. A,B and C. Following observations are recorded,
(a) Surface A. No photoemission occurs.
(b) Surface B. Photoemission occurs but the photoelectrons have zero kinetic energy.
(c) Surface C. Photoemission occurs and photoelectrons have some KE.
Based on Einstein's photoelectric equation, expalain the three observations.
To explain the observations based on Einstein's photoelectric equation, we can analyze each surface (A, B, and C) step by step.
1. Understanding Einstein's Photoelectric Equation:
The photoelectric effect can be described by Einstein's equation:
KEmax=hν−ϕ
where:
- KEmax is the maximum kinetic energy of the emitted photoelectrons,
- h is Planck's constant (6.626×10−34J⋅s),
- ν is the frequency of the incident radiation,
- ϕ is the work function of the material (the minimum energy required to remove an electron from the surface).
2. Observation for Surface A:
- Observation: No photoemission occurs.
- Explanation: This means that the energy of the incident photons (hν) is less than the work function (ϕ) of surface A. Therefore, the frequency of the incident radiation is below the threshold frequency (ν0) required for photoemission. Mathematically, we can say:
hν<ϕ⇒No photoemission
3. Observation for Surface B:
- Observation: Photoemission occurs, but the photoelectrons have zero kinetic energy.
- Explanation: Here, the energy of the incident photons is exactly equal to the work function of surface B. This means that all the energy of the photon is used to overcome the work function, leaving no excess energy for kinetic energy. Thus:
hν=ϕ⇒KEmax=0
4. Observation for Surface C:
- Observation: Photoemission occurs, and photoelectrons have some kinetic energy.
- Explanation: In this case, the energy of the incident photons is greater than the work function of surface C. This means that after overcoming the work function, there is some energy left, which translates into the kinetic energy of the emitted photoelectrons. Therefore:
hν>ϕ⇒KEmax>0
Summary of Observations:
- Surface A: hν<ϕ → No photoemission.
- Surface B: hν=ϕ → Photoemission occurs, KEmax=0.
- Surface C: hν>ϕ → Photoemission occurs, KEmax>0.
The photoelectric effect can be described by Einstein's equation:
KEmax=hν−ϕ
where:
- KEmax is the maximum kinetic energy of the emitted photoelectrons,
- h is Planck's constant (6.626×10−34J⋅s),
- ν is the frequency of the incident radiation,
- ϕ is the work function of the material (the minimum energy required to remove an electron from the surface).
- Observation: No photoemission occurs.
- Explanation: This means that the energy of the incident photons (hν) is less than the work function (ϕ) of surface A. Therefore, the frequency of the incident radiation is below the threshold frequency (ν0) required for photoemission. Mathematically, we can say:
hν<ϕ⇒No photoemission
- Observation: Photoemission occurs, but the photoelectrons have zero kinetic energy.
- Explanation: Here, the energy of the incident photons is exactly equal to the work function of surface B. This means that all the energy of the photon is used to overcome the work function, leaving no excess energy for kinetic energy. Thus:
hν=ϕ⇒KEmax=0
- Observation: Photoemission occurs, and photoelectrons have some kinetic energy.
- Explanation: In this case, the energy of the incident photons is greater than the work function of surface C. This means that after overcoming the work function, there is some energy left, which translates into the kinetic energy of the emitted photoelectrons. Therefore:
hν>ϕ⇒KEmax>0
- Surface A: hν<ϕ → No photoemission.
- Surface B: hν=ϕ → Photoemission occurs, KEmax=0.
- Surface C: hν>ϕ → Photoemission occurs, KEmax>0.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - NCERT Exerciese question1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Short answer1videos
DUAL NATURE OF RADIATION AND MATTER
- BOOK - PRADEEPCHAPTER - CURRENT ELECTRICITYEXERCISE - Problems for Practice (B)2videos
CURRENT ELECTRICITY
- BOOK - PRADEEPCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - Multiple Choice Questions1videos
ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENT
Similar Questions
Radiation of frequency 1015 Hz is incident on two photosensitive surfaces P and Q. there is no photoemission from surface P. photoemission occurs from surface Q but photoelectrons have zero kinetic energy. Explain these observations and find the value of work function for surface Q.
View Solution(i) State two important features of Einstein's photoelectric equation.
(ii) Radiation of frequency 1015Hz is incident on two photosenstive surface P and Q. There is no photoemission from surface P. Photoemission occurs from Q but photoelectrons have zero kinetic energy. Explain these observation and find the value of work function for surface Q.View Solution
Knowledge Check
- Question 1 - Select One
Radiations of frequencies 8×1015 Hz and 5×1015 Hz are incident one after the another on the same photosensitive surface. If is found that the kinetic energies of the photo electrons emitted from the surface are in the ratio of 2:1 . What is the threshold frequency for the surface ?
A1.5×1015HzB2×1015 HzC2.5×1015 HzD3×1015Hz - Question 2 - Select One
Radiation of frequency v=9v0 is incident on a metal surface, having threshold frequency v0. The maximum velocity of the ejected photoelectrons is 6×106m/s. What will be the maximum velocity of the ejected photoelectrons , if v is reduced to 3v0 ?
A2×106 m/sB3×106 m/sC1.5×106 m/sD4×106 m/s - Question 3 - Select One
Photoelectron emission is observed for three different metals A,B and C. the kinetic energy of the fastest photoelectrons versus frequency 'v' is plotted for each metal. Which of the following graphs can be observed?
A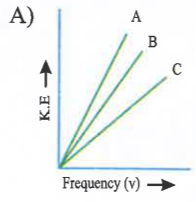 B
B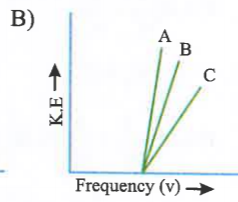 C
C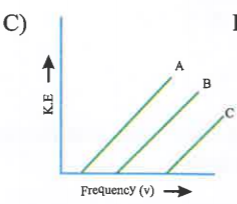 D
D
Two photosensitive X and Y are exposed to radiations of frequency 1012Hz. Comment on threshold frequency of each surface if photoelectrons emitted from surface X have zero kinetic energy and that from surface Y have some positive kinetic energy .
View SolutionWhy photoelectrons ejected from a metal surface have different kinetic energies although the frequency of incident photons are same ?
View SolutionA photon of wavelength 5000λ strikes a metal surface with work function 2.20eV calculate
aTHe energy of the photon in eV
b. The kinetic energy of the emitted photo electron
c. The velocity of the photoelectronView SolutionThe work function of a surface is 3.1 eV. A photon of frequency1x1015Hz. Is incident on it. Calculate the incident wavelength is photoelectric emission occur or not.
View SolutionWhen a high frequency electromagnetic radiation is incident on a metallic surface, electrons are emitted from the surface. Energy of emitted photoelectrons depends only on the frequency of incident electromagnetic radiation and the number of emitted electrons depends only on the intensity of incident light.
Einstein's protoelectron equation [Kmax=hv−ϕ} correctly ecplains the PE, where υ= frequency of incident light and ϕ= work function.
Q. Light of wavlength 3300 is incident on two metals A and B, whose work function are 4 eV and 2 eV, respectively. ThenView Solution

