Radius of earth is 6400 km while the radius of another planet is around 2800 km. The density of this planet is only 20% of the density of earth. The value of acceleration due to gravity of this planet is.
8.6
The correct Answer is:B
To find the acceleration due to gravity on the new planet, we can follow these steps:
1. Understand the formula for acceleration due to gravity (g):
The acceleration due to gravity on the surface of a planet is given by the formula:
g=G⋅MR2
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
2. Express mass in terms of density and volume:
The mass M of the planet can be expressed as:
M=Density×Volume
The volume V of a sphere is given by:
V=43πR3
Therefore, the mass can be rewritten as:
M=ρ⋅43πR3
3. Substituting mass into the gravity formula:
Substituting the expression for mass into the gravity formula gives:
g=G⋅ρ⋅43πR3R2
Simplifying this, we find:
g=43G⋅ρ⋅πR
4. Calculate the density of the new planet:
Given that the density of the new planet is 20% of the density of Earth, we can express this as:
ρplanet=0.2⋅ρEarth
5. Substituting the radius and density into the formula:
The radius of the new planet is given as 2800 km (or 2.8 x 10^6 meters). Substituting the density and radius into the gravity formula, we have:
gplanet=43G⋅(0.2⋅ρEarth)⋅π⋅(2.8×106)
6. Relate it to Earth's gravity:
We know that:
gEarth=43G⋅ρEarth⋅π⋅(6400×103)
Therefore, we can express gplanet in terms of gEarth:
gplanet=0.2⋅RplanetREarth⋅gEarth
Substituting the values:
gplanet=0.2⋅28006400⋅gEarth
7. Calculating the final value:
Simplifying:
gplanet=0.2⋅0.4375⋅gEarth
gplanet=0.0875⋅gEarth
Assuming gEarth≈9.8m/s2:
gplanet≈0.0875⋅9.8≈0.8575m/s2
8. Final approximation:
Rounding off gives:
gplanet≈8.6m/s2
Final Answer:
The value of acceleration due to gravity on this planet is approximately 8.6 m/s².
The acceleration due to gravity on the surface of a planet is given by the formula:
g=G⋅MR2
where G is the gravitational constant, M is the mass of the planet, and R is the radius of the planet.
The mass M of the planet can be expressed as:
M=Density×Volume
The volume V of a sphere is given by:
V=43πR3
Therefore, the mass can be rewritten as:
M=ρ⋅43πR3
Substituting the expression for mass into the gravity formula gives:
g=G⋅ρ⋅43πR3R2
Simplifying this, we find:
g=43G⋅ρ⋅πR
Given that the density of the new planet is 20% of the density of Earth, we can express this as:
ρplanet=0.2⋅ρEarth
The radius of the new planet is given as 2800 km (or 2.8 x 10^6 meters). Substituting the density and radius into the gravity formula, we have:
gplanet=43G⋅(0.2⋅ρEarth)⋅π⋅(2.8×106)
We know that:
gEarth=43G⋅ρEarth⋅π⋅(6400×103)
Therefore, we can express gplanet in terms of gEarth:
gplanet=0.2⋅RplanetREarth⋅gEarth
Substituting the values:
gplanet=0.2⋅28006400⋅gEarth
Simplifying:
gplanet=0.2⋅0.4375⋅gEarth
gplanet=0.0875⋅gEarth
Assuming gEarth≈9.8m/s2:
gplanet≈0.0875⋅9.8≈0.8575m/s2
Rounding off gives:
gplanet≈8.6m/s2
The value of acceleration due to gravity on this planet is approximately 8.6 m/s².
Topper's Solved these Questions
- NSO QUESTION PAPER 2020 SET 2BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2020 SET 2EXERCISE - ACHIEVERS SECTION
1 Videos
- NSO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - NSO QUESTION PAPER 2020 SET 1EXERCISE - ACHIEVERS SECTION
1 Videos
- SAMPLE PAPER 4 (CLASS 10)BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - SAMPLE PAPER 4 (CLASS 10)EXERCISE - Section C- Science
4 Videos
Similar Questions
The density of a planet is doubled without changing its radius. How wil it effect the acceleration due to gravity in the planet?
View SolutionSuppose a planet exists whose mass and radius both, are half those of earth. Calculate the acceleration due to gravity on the surface of this planet.
View Solution
Knowledge Check
If the density of the planet is double that of the earth and the radius 1.5 times that of the earth, the acceleration due to gravity on the planet is
A4/3 times that on the surface of the earthB3 times that on the surface of the earthC3/4 times that on the surface of the earthD6 times that on the surface of the earthIf the density of a planet is constant, then the curve between value of g on its surface and its radius r will be-
A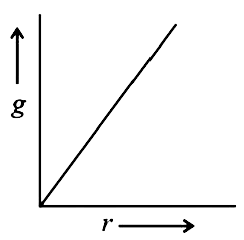 B
B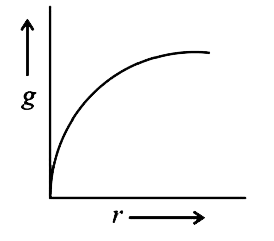 C
C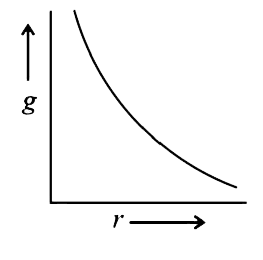 D
D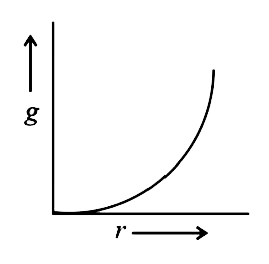
The mass of a planet is twice the mass of earth and diameter of the planet is thrie the diameter of the earth, then the acceleration due to gravity on the planet's surface is
Ag/2B2gC2g/9D3g/√2
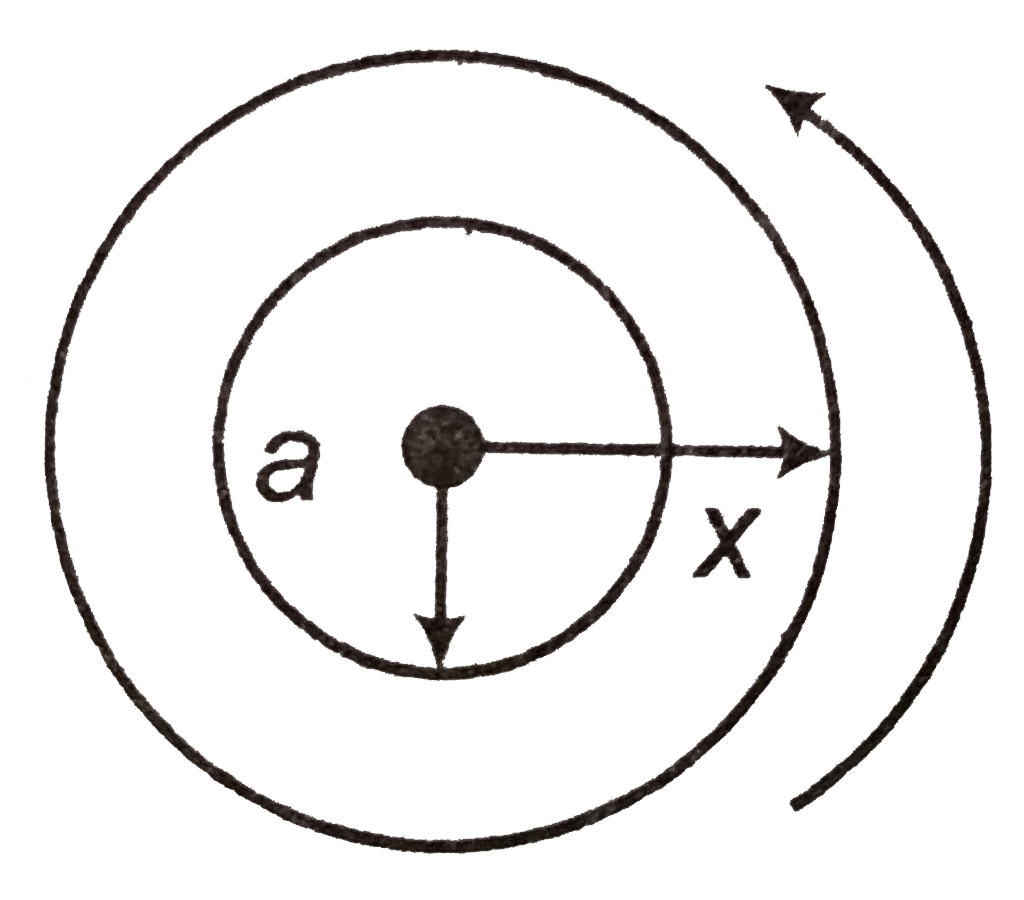
The radius of a planet is a. satelite revolves around it in a circle of radius x with angular velocity ω. The acceleration due to the gravity on planet's surface is
View SolutionIf the mass of earth is eighty times the mass of a planet and diameter of the planet is one fourth that of earth, then acceleration due to gravity on the planet would be
View SolutionIf the mass of a planet is 10% less than that of the earth and the radius is 20% greater than that of the earth, the acceleration due to gravity on the planet will be
View SolutionIf the radius of the earth is 6400 km, the height above the surface of the earth where the value of acceleration due to gravity will be 4% of its value on the surface of the earth is
View SolutionThe radius of a planet is n times the radius of earth (R). A satellite revolves around it in a circle of radius 4nR with angular velocity ω. The acceleration due to gravity on planet's surface is
View Solution
