Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Derive the expression for the magnitude of →B at any point on the x-axis in terms of the x-coordinate of the point. What is the direciton of →B?
A
√2μ0Iaπ(x2+a2)
B
3μ0Iaπ(x2+a2)
C
μ0Ia2π(x2+a2)
D
μ0Ixπ(x2+a2)
Video Solution
Text Solution
The correct Answer is:D
(d) 
At a position on the x-axis:
Bnet=2μ0I2πrcosθ=μ0Iπ(√x2+a2)a√x2+a2
Bnet=μ0Ixπ(x2+a2)
It's graphs is shown below.

The magnetic field is a maximum when :
dBdx=0=Cx2+a2−2Cx2(x2+a2)2
(x2+a2)=2x2⇒x=±a
When x>>a,B≈μ0Iπx,
which is just like a wire carrying current 2I.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)7videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)1videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )2videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Knowledge Check
- Question 1 - Select One
Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
At what value of x is the magnitude of →B is maximum?Ax=0Bx=√2aCx=±a/2Dx=±a - Question 2 - Select One
Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Graph the magnitude of →B at points on the x-axis.A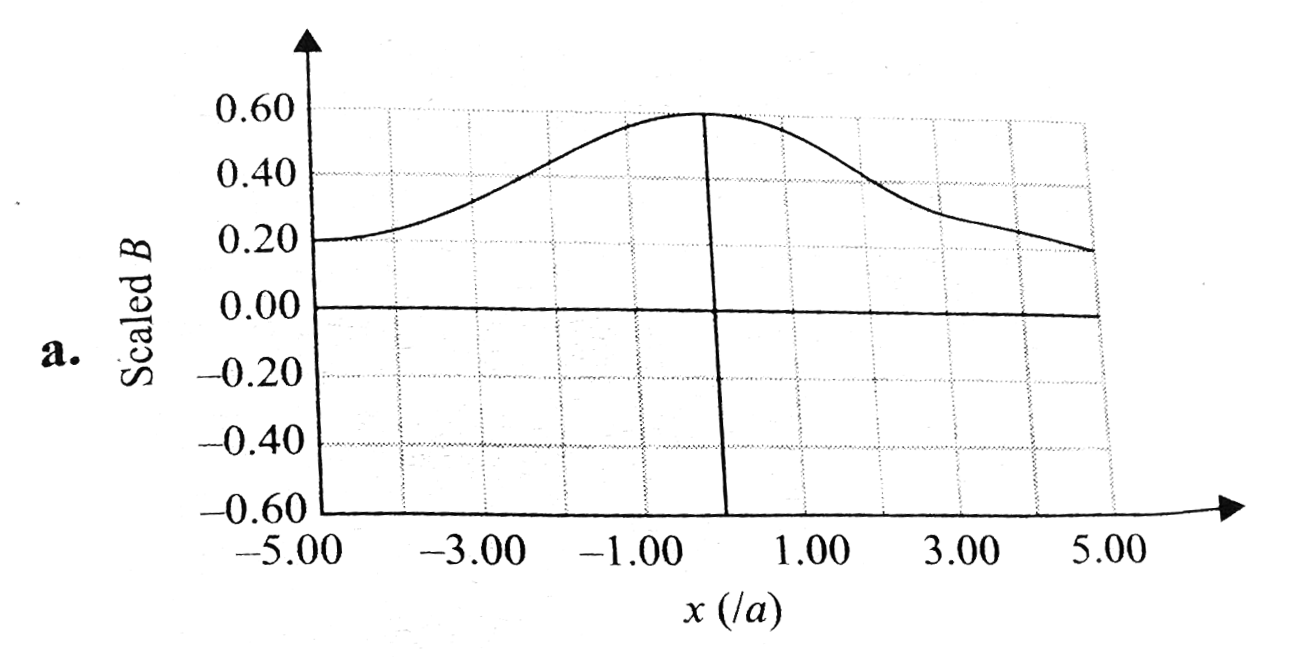 B
B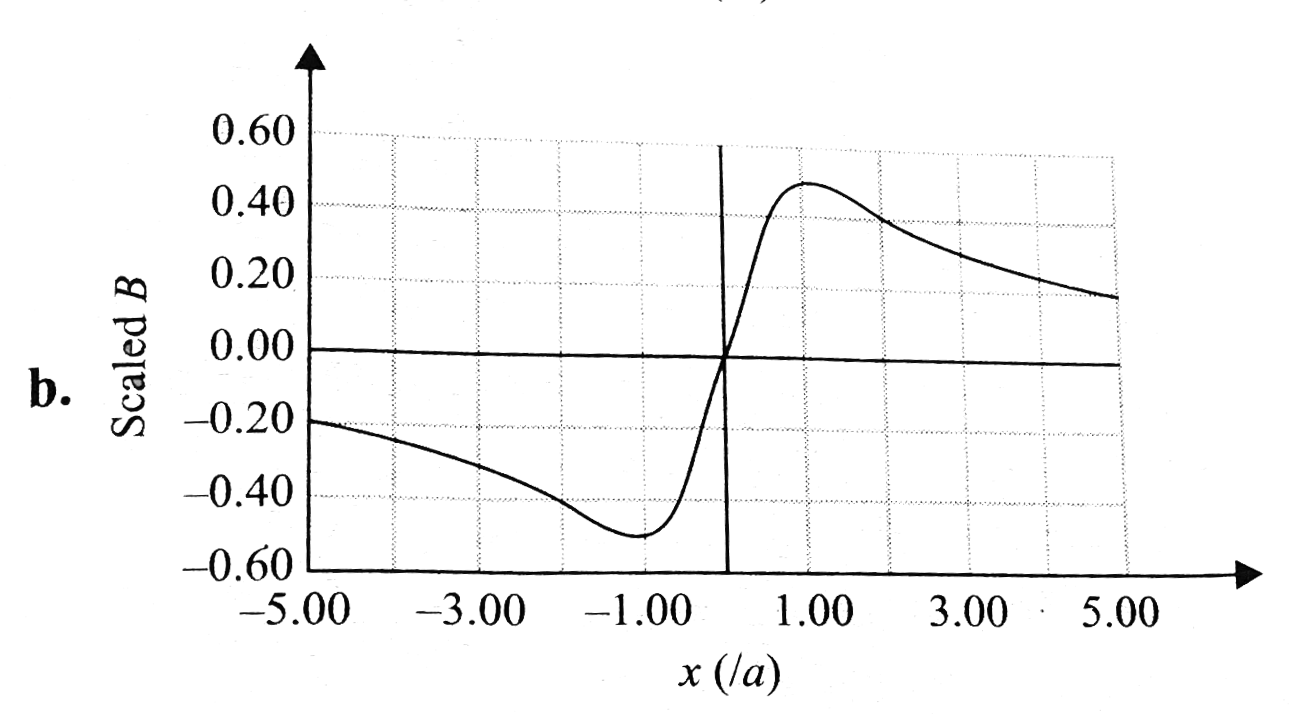 C
C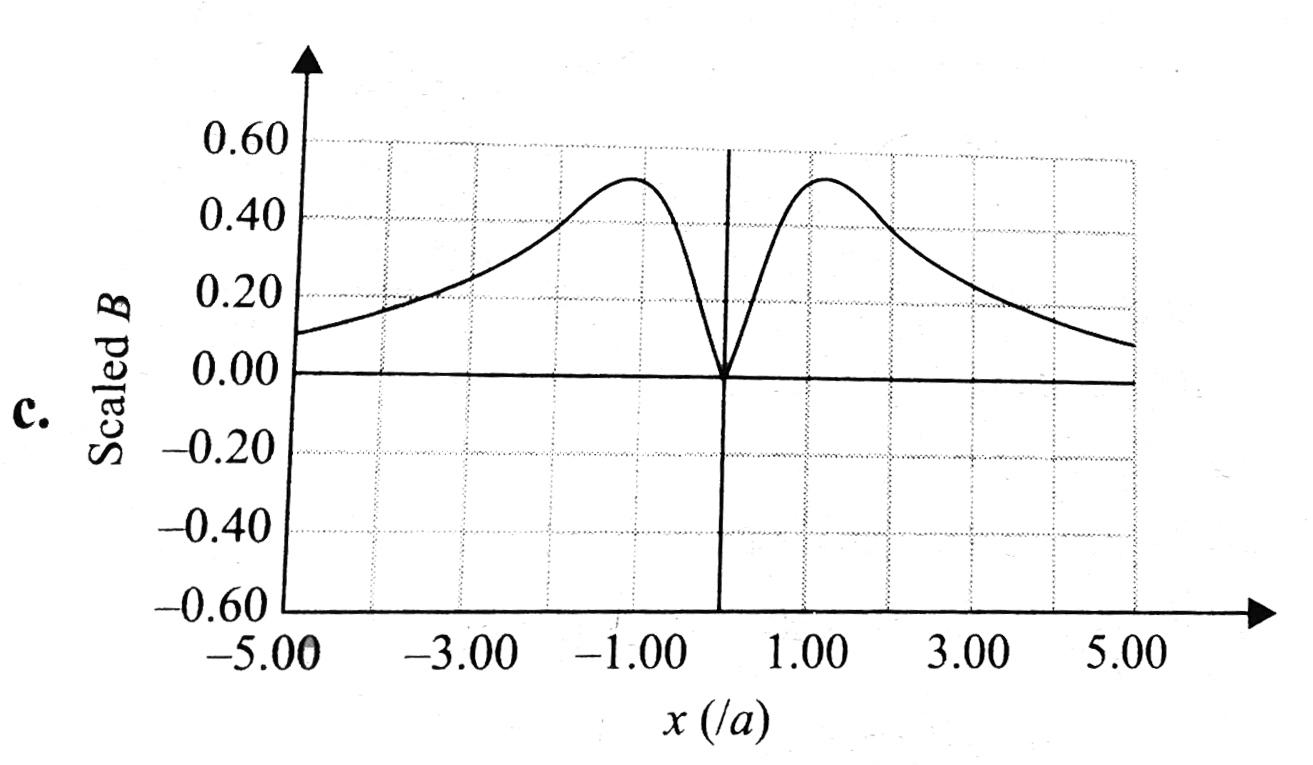 D
D
- Question 3 - Select One
Figure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

Derive an expression for the magnitude of →B at any point on the x-axis in terms of the x-coordinate of the point. What is the direction of →B?A√2μ0Iaπ(x2+a2)B3μ0Iaπ(x2+a2)Cμ0Ia2π(x2+a2)Dμ0Iaπ(x2+a2)
A point is on the x axis what are its y coordinate and z coordinates
View SolutionWhat is the y-coordinate of every points on X-axis ?
View SolutionWhat is the x -coordinate of every point on Y-axis ?
View Solution50 A current in north to south direction. Give the magnitude and direction of →B at a point2.5 m east of the wire.
View SolutionFigure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.

Graph the magnitude of →B at point on the x-axis.View Solution

