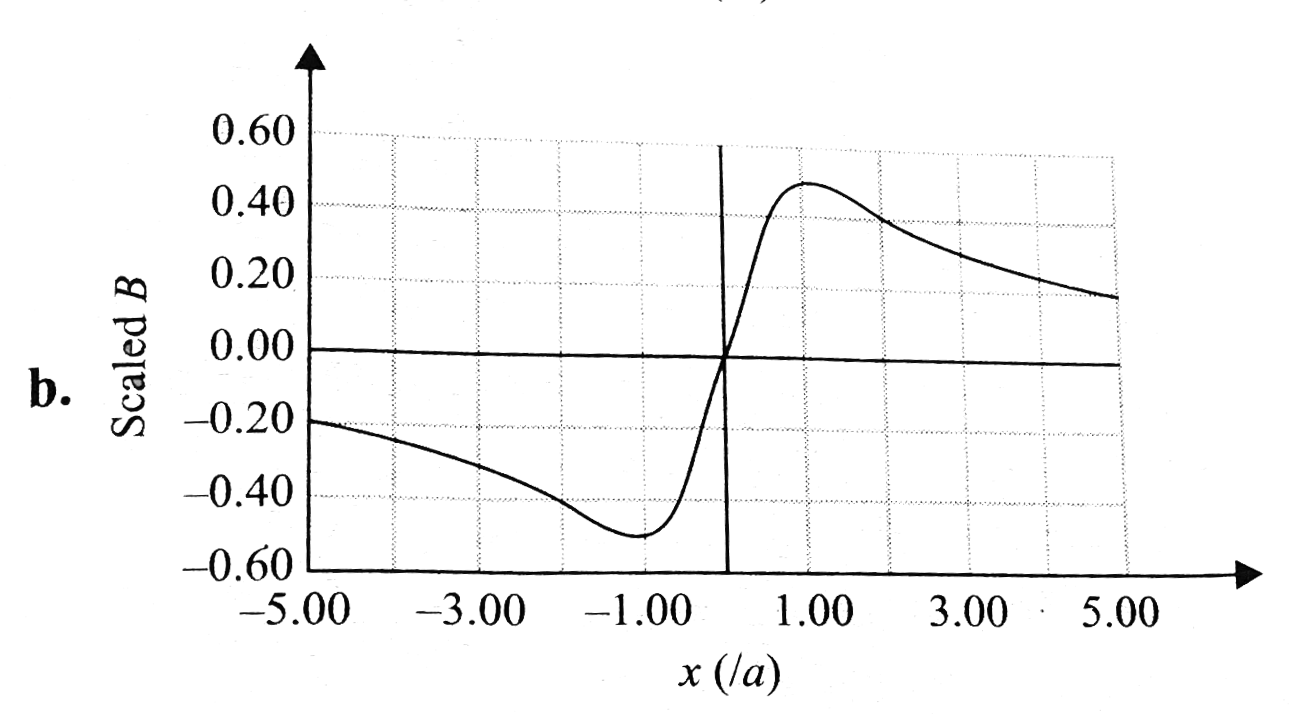
Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
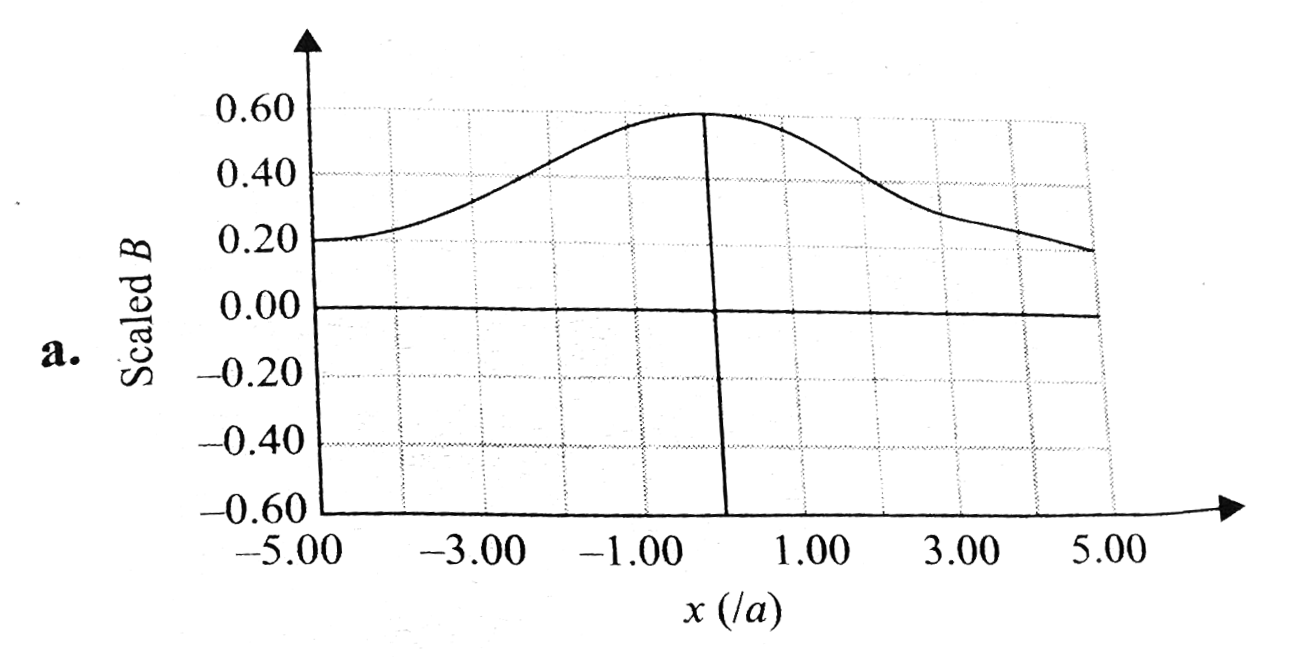
Graph the magnitude of →B at points on the x-axis.
The correct Answer is:B
(b) 
At a position on the x-axis:
Bnet=2μ0I2πrcosθ=μ0Iπ(√x2+a2)a√x2+a2
Bnet=μ0Ixπ(x2+a2)
It's graphs is shown below.
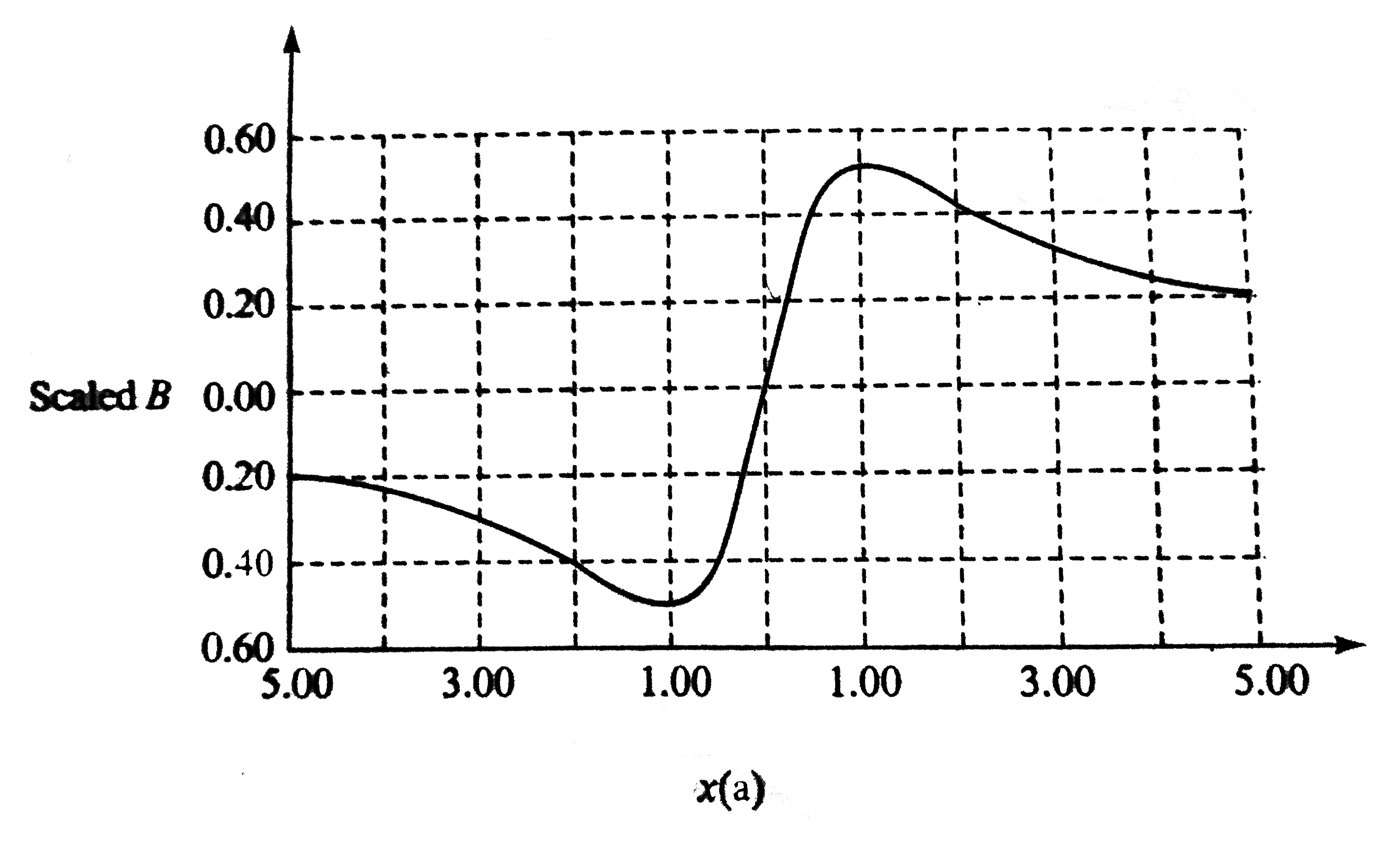
The magnetic field is a maximum when :
dBdx=0=Cx2+a2−2Cx2(x2+a2)2
(x2+a2)=2x2⇒x=±a
When x>>a,B≈μ0Iπx,
which is just like a wire carrying current 2I.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (integer)7videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Archives (fill In The Blanks)1videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Exercise (assertion-reasioning )2videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICSCHAPTER - SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - QUESTION BANK12videos
SEMICONDUCTOR ELECTRONIC : MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - CENGAGE PHYSICSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Question Bank40videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Six long parallel current carrying wires are perpendicular to the plane of the fig. They pass through the vertices of a regular hexagon of side length a. All wires have same current I. Direction of current is out of the plane of the figure in all the wires except the one passing through vertex F, which has current directed into the plane of the figure. Calculate the magnetic induction field at the centre of the hexagon. Also tell the direction of the field.
View SolutionTwo long, straight wires a and b are 2⋅0 m apart,
perpendicular to the plane of the paper as shown in figure
. The wire a carries a current of 9⋅6A directed
into the plane of the figure,The magnetic field at the
point P at a distance of 10/11 m from the wire b is zero.
Find (a) the magnitude and direction of the current in b,
(b) the magnitude of the magnetic field B at the point s
and (c) the force per unit length on the wire b.
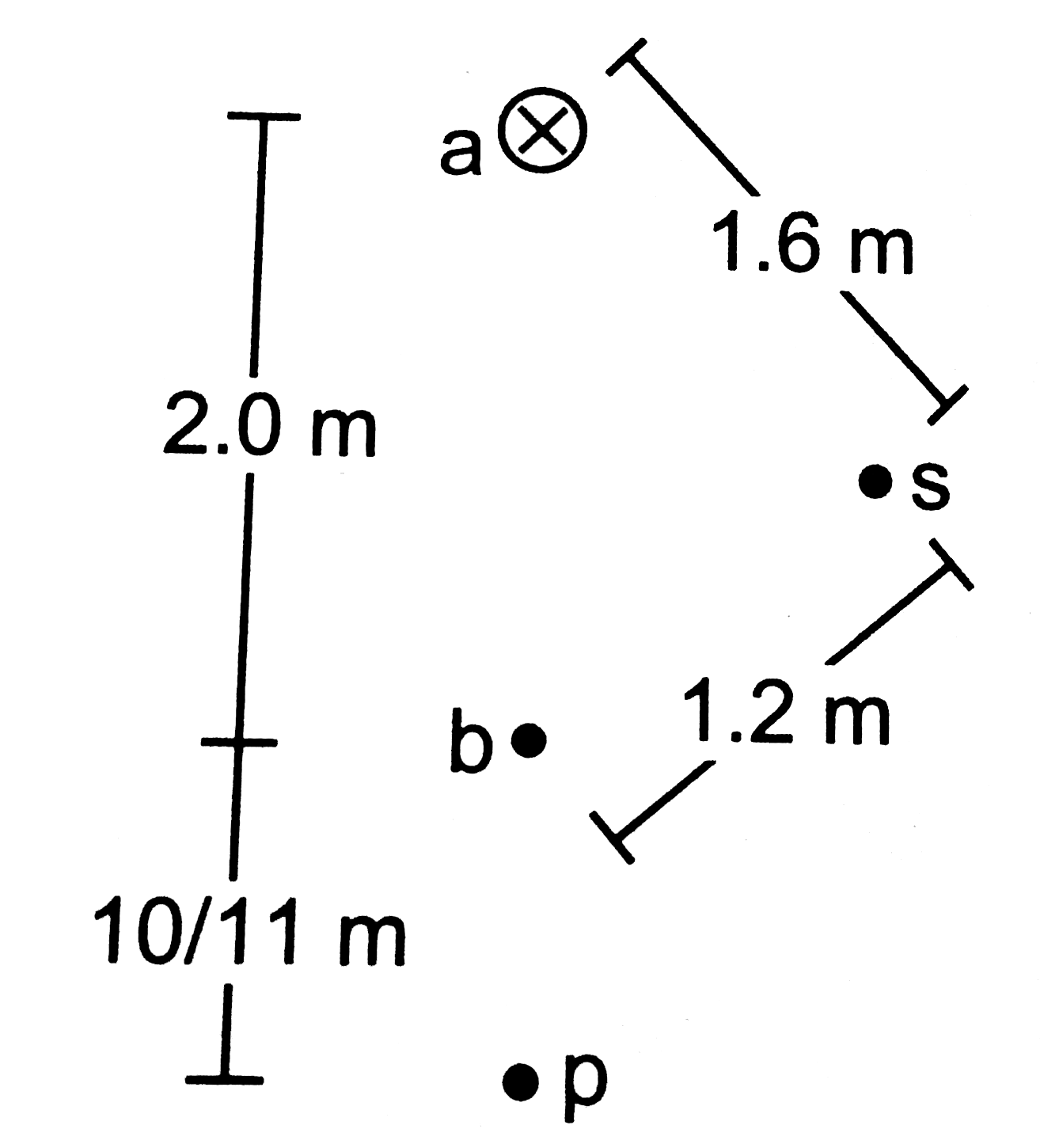View Solution
Knowledge Check
- Question 1 - Select One
Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
At what value of x is the magnitude of →B is maximum?Ax=0Bx=√2aCx=±a/2Dx=±a - Question 2 - Select One
Repeat the above problem, but with the current in both wires shown in fig. directed into the plane of the figure.
Derive the expression for the magnitude of →B at any point on the x-axis in terms of the x-coordinate of the point. What is the direciton of →B?A√2μ0Iaπ(x2+a2)B3μ0Iaπ(x2+a2)Cμ0Ia2π(x2+a2)Dμ0Ixπ(x2+a2) - Question 3 - Select One
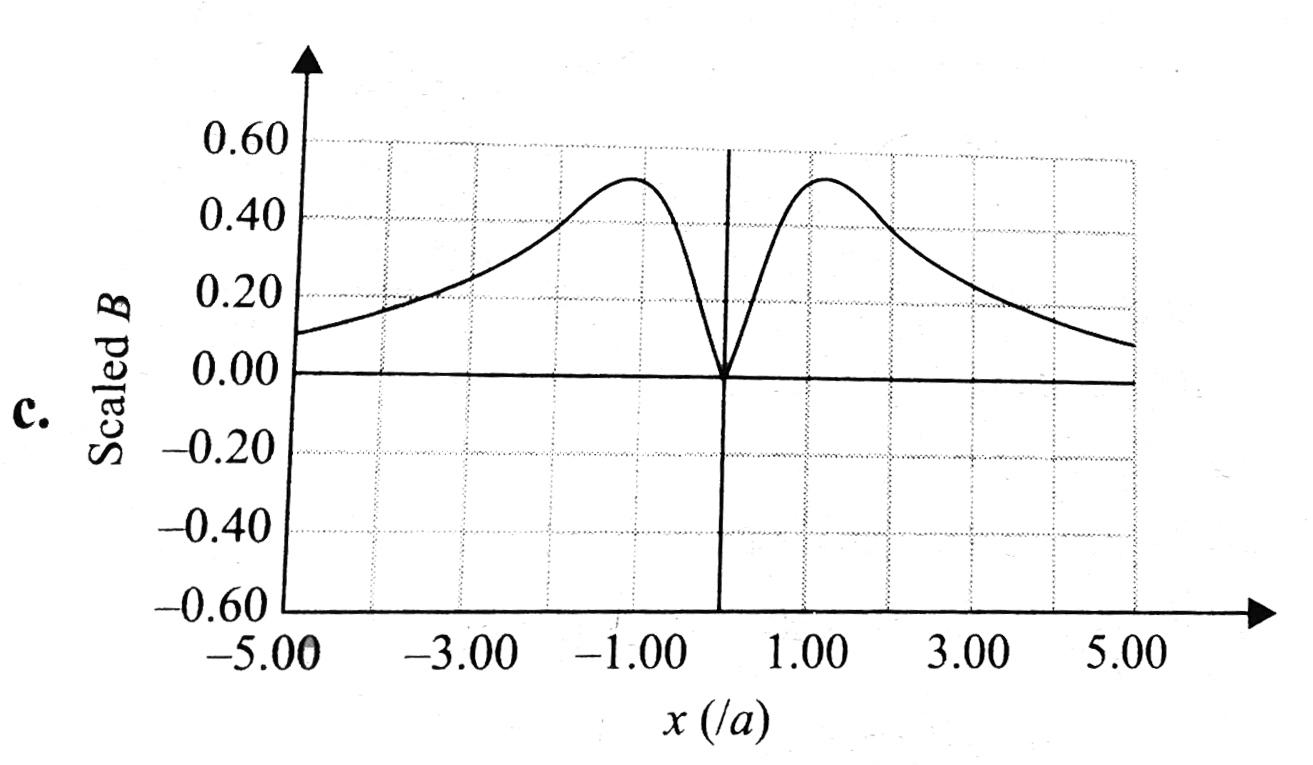
Figure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.
Graph the magnitude of →B at point on the x-axis.A
B
C
D
50 A current in north to south direction. Give the magnitude and direction of →B at a point2.5 m east of the wire.
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
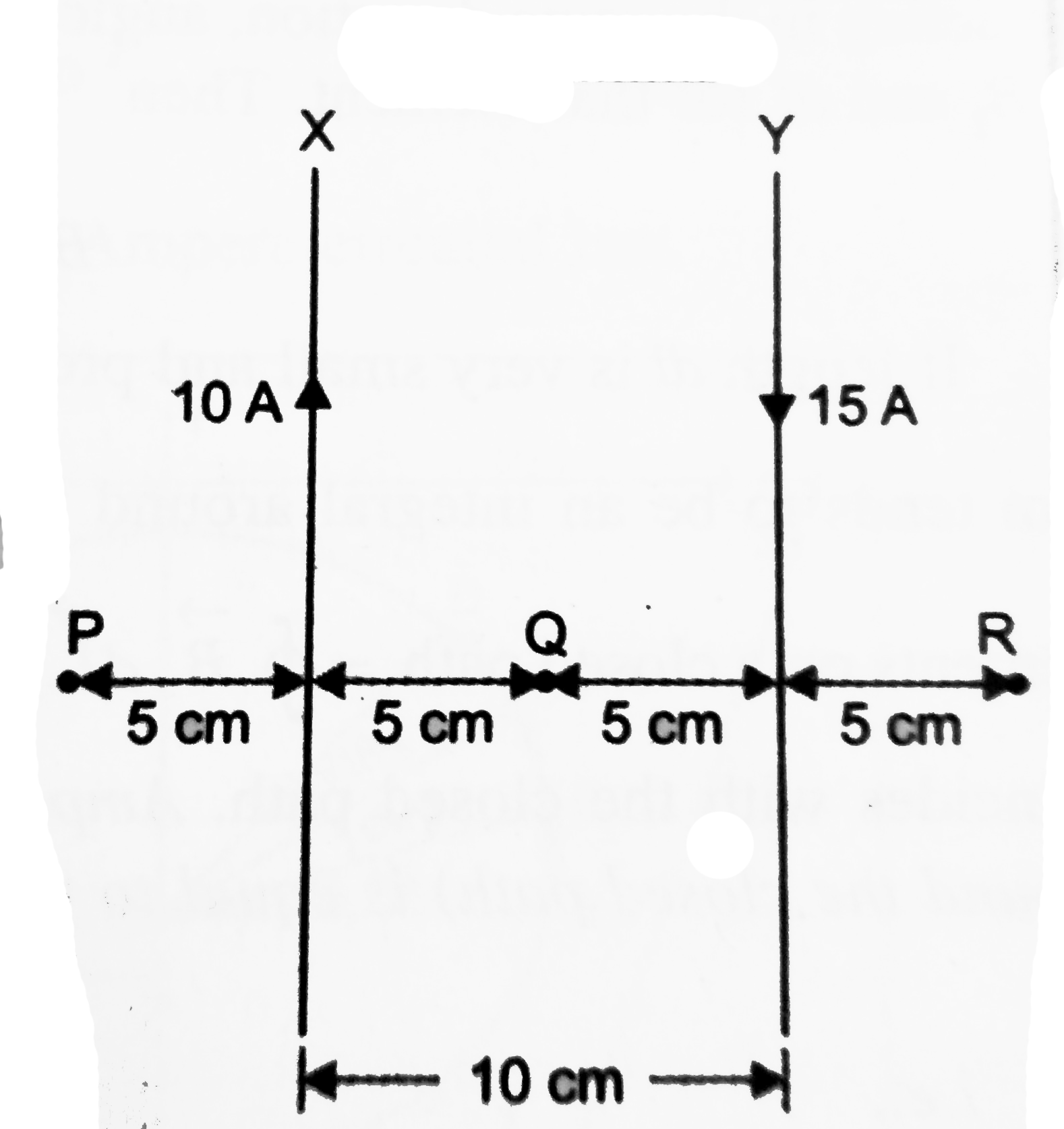View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be
View SolutionFigure shows an end view of two long, parallel wires perpendicular to the xy plane, each carrying a current I, but in opposite directions.
Derive an expression for the magnitude of →B at any point on the x-axis in terms of the x-coordinate of the point. What is the direction of →B?View SolutionIn the above problem the direction of initial velocity with x-axis is:
View Solution